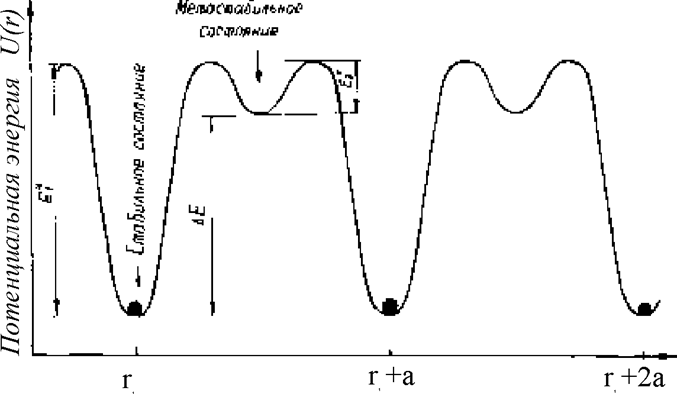
 |
Рис.1.5.12. Энергетический барьер при образовании точечных дефектов (а - параметр решетки в направлении г)
Вакансия мигрирует по объему как независимый вид нерелаксирующих дефектов.
Естественно, требуется заметно меньшая энергия для реализации процесса рождения вакансий по Шоттки из-за исключения необходимости полного разрыва всех связей при неполном испарении с поверхности.
 |
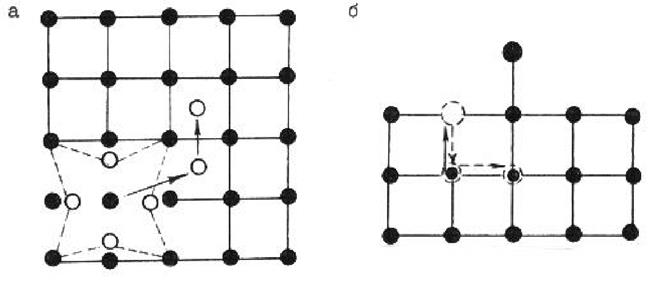а –“по Френкелю”, б –“по Шоттки''
Существует еще один тип дефектов, также называемых дефектами Шоттки. Это - пара вакансий противоположного знака. Действительно, возникновение вакансии, например, в решетке LiF за счет удаления иона Li+ из подрешетки лития приводит к появлению некомпенсированного отрицательного заряда.
Ион Li+ рано или поздно "найдет" себе электрон и превратится в нейтральный внедренный атом в объеме или выйдет на поверхность и пристроится к иону фтора. Для сохранения электронейтральности необходимо образование вакансии и в подрешетке фтора. В результате и возникнет пара противоположно заряженных вакансий - дефект Шоттки, в котором нарушается симметрия и компенсация электронного распределения. Эти дефекты играют очень важную роль в оптических свойствах и называются центрами окрашивания.
Как правило, лишь немногие атомы получают кинетическую энергию, достаточную для преодоления барьера Е1* (см. рис. 1.5.12). В дальнейшем существует разъединенная пара вакансия - дислоцированный атом. Вследствие миграции, более легкой для вакансии, в объеме будут существовать два точечных дефекта, если только не произойдет рекомбинация - одновременное исчезновение двух дефектов при случайной встрече.
Статистический расчет показывает, что в любой промежуток времени имеется некоторое значимое количество атомов, способных преодолеть потенциальный барьер. Количество таких атомов за 1 с составляет
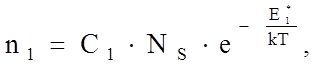(1.5.10)
где С1 - константа для данного типа решетки и данных атомов; NS - число атомов в стабильных положениях, k - постоянная Больцмана, T - температура, К.
Обратный переход в стабильное состояние (или близкий по энергии переход в соседнее метастабильное) требует меньшей энергии Е2*, что обозначает возможность обратного перехода за 1 с для числа атомов
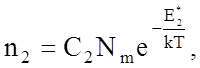(1.5.11)
где С2 - некоторая константа, Nm - число атомов в метастабильных состояниях.
Равновесную в данных условиях концентрацию дефектов можно найти из соотношения
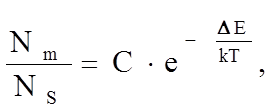(1.5.12)
где С - константа, определяемая из экспериментов, DЕ – энергия образования дефекта. Конечно, число атомов NS в стабильном положении мало отличается от общего числа равновесных мест в решетке N0. Если положить NS»N0»NA - числу Авогадро, числу атомов в моле вещества, то равновесную концентрацию дефектов можно найти из соотношения
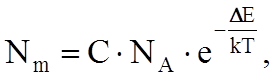
(1.5.13)
где DE = EФр - энергия образования френкелевской пары дефектов и DЕ =Eш , если это дефект Шоттки. EФр составляет от единиц до десятков электронвольт, например, в углеродной алмазной решетке ЕФр»60 эВ. ЕШ на один-два порядка меньше и в частности для Al составляет около 0,75 эВ. Если подставить это значение в уравнение (1.5.13) и положить Т1 = 300 К, то получим nШ = 1018 м-3 и при Т2 = Тпл = 923 К, nШ = 1025 м-3.
Сопоставим полученные данные с общим количеством N узлов решетки в 1 м3 Аl. Алюминий кристаллизуется в гранецентрированную решетку с параметром а = 4,04 Å, на одну ячейку которой приходится z = 4 атома. Число элементарных ячеек N` в любом объеме V здесь V = 1 м3, DV = а3 - объем одной ячейки. Общее число узлов N
 |
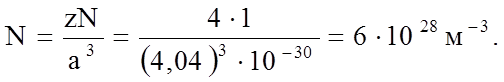Таким образом, равновесная концентрация вакансионных дефектов, являясь заметной уже при комнатной температуре, при повышении температуры быстро возрастает, достигая величины одной вакансии на каждые 6000 узлов при температуре плавления материала. Это значение близко для любых веществ вблизи температуры плавления.
Дефекты решетки по Френкелю и Шоттки оказывают большое влияние на оптические, механические, электрические и магнитные свойства кристаллов, но особенно - на диффузионные процессы. Очень важна их роль в поведении тонких пленок, аморфных и мелкокристаллических веществ.
П р и м е с и
Очистка веществ до степени, превышающей 10-9 атомных процентов, технически достаточно сложная задача даже в лабораторных условиях. Достичь такого уровня очистки - это все равно, что контролировать ситуацию, когда в 10 т пшеницы находится одно зерно ржи
(по образному выражению Г.Е.Епифанова). 10-9 атомных процентов примеси - это значит 1017 атомов примесей в 1 м3 вещества, 108 атомов примесей - в 1 мм3. Столь высокая степень очистки особенно необходима в полупроводниковых материалах.
Примеси могут находиться в кристалле в виде равномерно рассеянных по объему атомов, а могут - в виде компактных инородных включений почти сферической ("глобулярной") формы или в виде плоских скоплений. Характер распределения зависит от растворимости вещества примеси в матричном материале, способности образовывать с ним химические соединения, соотношения радиусов основного и примесного вещества, температуры и других факторов. Примесные атомы, не образующие отдельной фазы, могут быть представлены в объеме в виде атомов замещения и внедрения (см. рис. 1.5.11,б,в). Предельное количество их, до образования отдельной фазы, определяется с помощью диаграмм состояния, построенных экспериментально для очень многих двойных и тройных систем. Принципиальный вид участков диаграммы при ограниченной (а) и неограниченной (б) растворимости в твердой и жидкой фазе в зависимости от температуры представлен на рис. 1.5.14.
Твердые растворы внедрения подчиняются правилу ограниченной растворимости в решетках с плотной упаковкой и характерны для атомов с малым собственным радиусом - водорода, бора, углерода, азота и, в некоторых случаях, кислорода.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.