Разработка цифрового режекторного эллиптического (Чебышева-Кауэра) БИХ-фильтра

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ  УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

Дисциплина  «Теория  и  обработка  сигналов»,     6 - й семестр

КУРСОВАЯ  РАБОТА

Разработка цифрового  режекторного

эллиптического (Чебышева-Кауэра) БИХ-фильтра

Вариант 8

Выполнил:                                                                                          Преподаватель:

Спитченко  В.М.                                                                                доц. Щетинин Ю.И.

Группа: АИ-72

Новосибирск

2010

Содержание

Введение. 3

1. Задание. 4

2. Обоснование выбора и сущность метода проектирования. 4

3. Проектирование фильтра. 6

4. Реализация фильтра. 11

5. Тестирование  фильтра. 12

6. Программирование фильтра и оценка быстродействия. 16

Заключение. 18

Список используемой литературы.. 19

Введение

Цифровая обработка сигналов как направление развития науки и техники зародилась в 1950-х годах и поначалу представляла собой довольно экзотическую отрасль радиоэлектроники, практическая ценность которой была далеко не очевидной. Однако за прошедшие пятьдесят лет благодаря успехам микроэлектроники системы цифровой обработки сигналов не только воплотились в реальность, но и вошли в нашу повседневную жизнь в виде CD- и DVD-проигрывателей, модемов, сотовых телефонов и многого

другого [2].

Из всех задач, решаемых при цифровой обработке сигналов, наиболее важной является  задача фильтрации. Фильтром называется цепь (система, устройство), обеспечивающая необходимую реакцию на заданный входной сигнал. Основное применение фильтров заключается в выделении полезного сигнала из аддитивной смеси его с шумом. То есть фильтр преобразует входной сигнал таким образом, что определенные полезные гармоники входного сигнала сохраняются в выходном сигнале, а нежелательные подавляются.

Фильтры сигналов разделяются на аналоговые и цифровые. В аналоговых фильтрах производится преобразование аналоговых (непрерывных) сигналов. Цифровой фильтр, работающий в реальном масштабе времени, оперирует с дискретными по времени данными. При этом очередной отсчет, соответствующий отклику фильтра, формируется по окончании каждого периода дискретизации. Среди цифровых фильтров, в свою очередь, выделяют два фундаментальных класса: фильтры с конечной импульсной характеристикой (КИХ-фильтры или нерекурсивные) и фильтры с бесконечной импульсной характеристикой (БИХ-фильтры или рекурсивные) [2].

В зависимости от полосы частот прохождения сигнала фильтры подразделяются фильтры нижних частот (ФНЧ), верхних частот (ФВЧ), полосовые (ПФ) и режекторные (РФ, заграждающие) [2].

Для аппроксимации характеристик фильтров используются специальные типы функций, которые могут быть реализованы в практических схемах. По названию аппроксимирующих функций соответствующие фильтры называю фильтрами Баттерворта, Чебышева, Бесселя, Кауэра и др. [2].

Таким образом, в зависимости от требований, предъявляемых к выходному сигналу, используются те или иные фильтры. И в каждом конкретном случае требуется спроектировать цифровой фильтр с теми или иными характеристиками, удовлетворяющими этим требованиям.

В данной курсовой работе, проектируется цифровой эллиптический режекторный  БИХ - фильтр (Чебышева-Кауэра) с помощью системы MatLab 7.0 и системы Borland C++ Builder 6, используемой для оценки быстродействия фильтра.

1. Задание

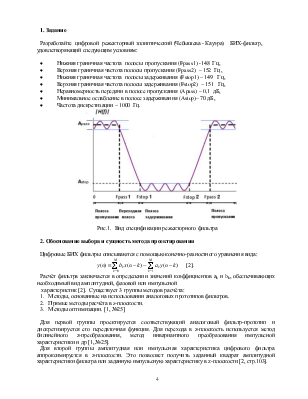
Разработайте  цифровой  режекторный эллиптический (Чебышева - Кауэра)    БИХ-фильтр, удовлетворяющий следующим условиям:

·  Нижняя граничная частота  полосы  пропускания (Fpass1) -148  Гц,

·  Верхняя граничная частота полосы пропускания (Fpass2)  – 152  Гц,

·  Нижняя граничная частота  полосы задерживания (Fstop1) – 149   Гц,

·  Верхняя граничная частота полосы задерживания (Fstop2)  – 151   Гц,

·  Неравномерность передачи в полосе пропускания (Apass) – 0,1  дБ,

·  Минимальное ослабление в полосе задерживания (Astop)– 70 дБ,

·  Частота дискретизации – 1000  Гц.

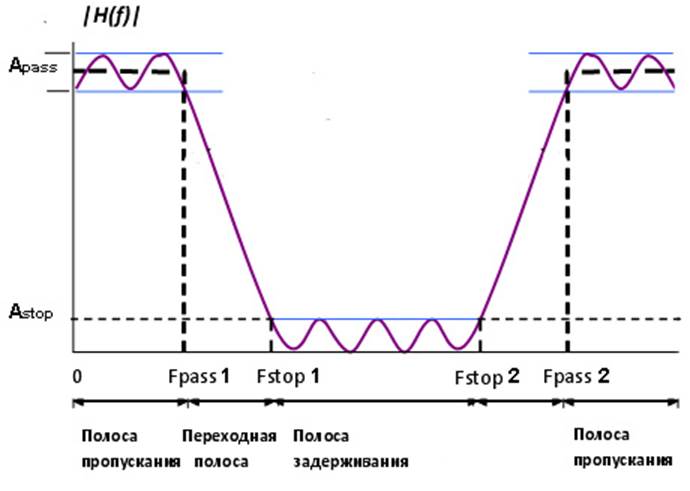
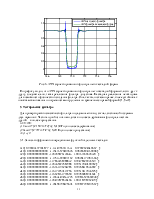
Рис.1.  Вид спецификации режекторного фильтра

2. Обоснование выбора и сущность метода проектирования

Цифровые БИХ фильтры описываются с помощью конечно-разностного уравнения вида:

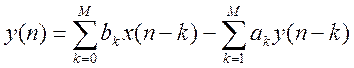                                            [2].

Расчёт фильтра заключается в определении значений коэффициентов а_k и b_k, обеспечивающих необходимый вид амплитудной, фазовой или импульсной

 характеристик [2].  Существует 3 группы методов расчёта:

1.  Методы, основанные на использовании аналоговых прототипов фильтров.

2.  Прямые методы расчёта в z-плоскости.

3.  Методы оптимизации. [1, №25]

Для первой группы проектируется соответствующий аналоговый фильтр-прототип и дискретизируется его передаточная функция. Для перехода в z-плоскость используется метод билинейного z-преобразования, метод инвариантного преобразования импульсной характеристики и др [1, №25].

Для второй группы амплитудная или импульсная характеристика цифрового фильтра аппроксимируется в z-плоскости. Это позволяет получить заданный квадрат амплитудной характеристики фильтра или заданную импульсную характеристику в z-плоскости [2, стр.103].

Для третьей группы применяются сложные методы оптимизации, минимизирующие отклонение аппроксимирующей характеристики от заданной характеристики фильтра [2, стр.94].

Наиболее распространены методы расчета БИХ-фильтров, вклю­чающие проектирование соответствующего аналогового прототипа, т.к. разработка аналоговых прототипов раньше предшествовала цифровым фильтрам и их методы расчета хо­рошо известны. Этот метод проектирования можно разделить на этапы:

- используя спецификации цифрового фильтра, необходимо получить спецификации аналогового фильтра;

- проектирование аналогового фильтра, а именно нормированного фильтра нижних частот;

- переход от НФНЧ к целевому фильтру.

Такой переход от НФНЧ к целевому фильтру осуществляется путем введения замены типа 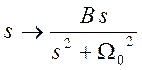  в передаточной функции НФНЧ  [1, № 24].

Синтез аналогового фильтра включает следующие  этапы: