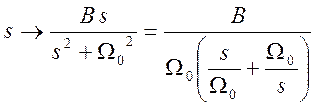Информатика и выч. техника \ Теория и обработка сигналов

Разработка цифрового режекторного эллиптического (Чебышева-Кауэра) БИХ-фильтра, страница 3

, где ,     [1, № 24]

Это преобразование сопровождается удвоением порядка,   в результате аналоговый РФ имеет уже 12-й порядок  (N =12). [1, № 26]

% построение АЧХ и ЛАЧХ аналогового РФ:

[H, W] = freqs(num, den, 4096);

figure(2)

subplot(2,1,1);

plot (W, abs(H))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('График АЧХ аналогового РФ');

subplot(2,1,2);

plot (W, 20*log10(abs(H)))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('График ЛАЧХ аналогового РФ');

xlabel('w, рад');

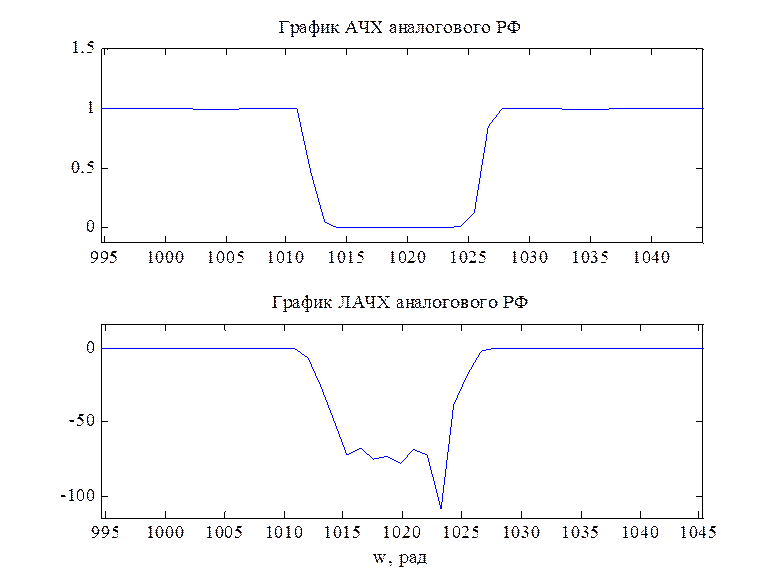
Рис.3. Графики АЧХ и ФЧХ аналогового режекторного фильтра

3.7. Трансформирование  аналогового РФ в цифровой с помощью билинейного преобразования

[numd, dend]=bilinear(num, den, Ft)   %   получаем коэффициенты целевого  фильтра

Уравнение фильтра 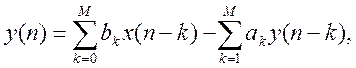где bk – элементы вектора numd,  ak –элементы вектора dend.

numd =    0.9650   -6.8068   25.7948  -65.3900  122.1406 -175.1364  197.1685

               -175.1364  122.1406  -65.3900   25.7948   -6.8068    0.9650

dend =    1.0000   -7.0252   26.5156  -66.9471  124.5471 -177.8709  199.4444

              -176.4485  122.5632  -65.3539   25.6776   -6.7488    0.9530

3.8. Построение АЧХ  цифрового РФ

%  построение АЧХ аналогового РФ

format long;

[numd, dend]=bilinear(num, den, Ft)

[H, f]=freqz(numd, dend, 4096*10,Ft);

figure(3)

subplot(2,1,1);

plot(f, abs(H));

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('АЧХ цифрового РФ')

subplot(2,1,2), plot(f, 20*log10(abs(H)))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('ЛАЧХ цифрового РФ')

xlabel('f , Гц')

ylabel('дБ')

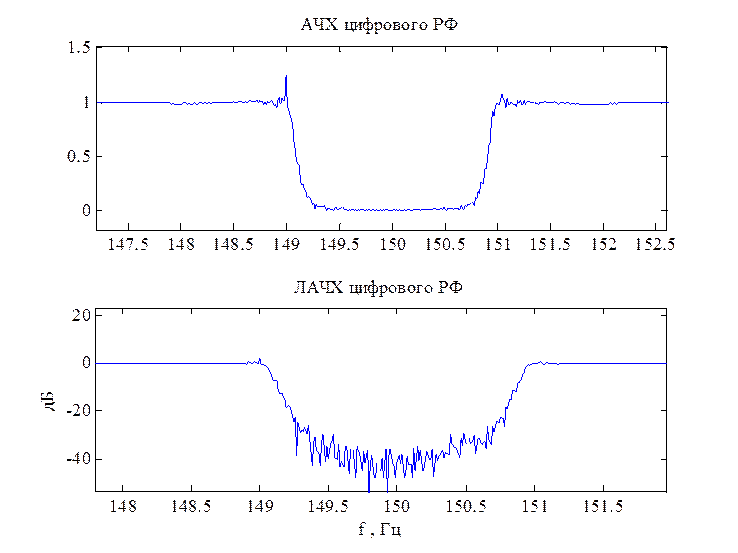
Рис. 4. АЧХ цифрового режекторного фильтра

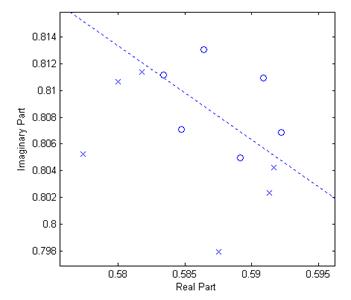3.9. Построение диаграммы нулей и полюсов

figure(4)

zplane(numd, dend);

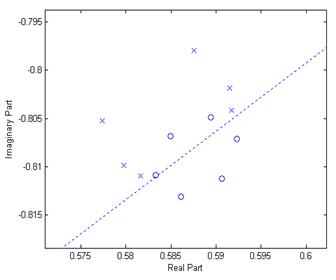
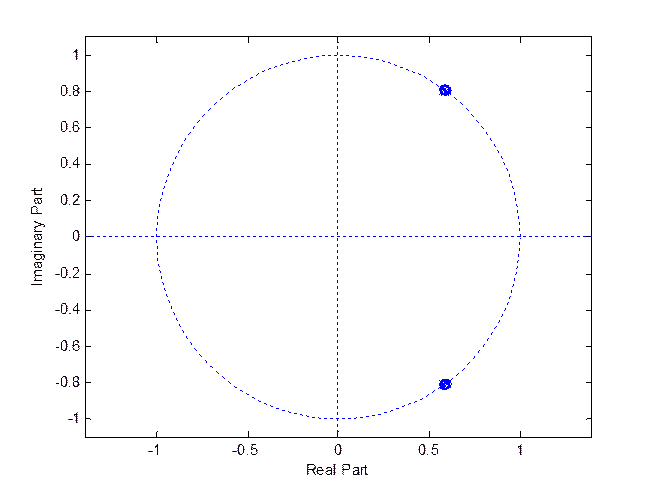
Рис. 5. Диаграмма нулей и полюсов

Видно, что система устойчива, так как все полюса лежат внутри единичной окружности. По рисункам 2 и 3 можно видеть, что характеристики цифрового фильтра соответствуют исходной спецификации.

4. Реализация фильтра

        Последовательная форма реализации цифрового фильтра менее чувствительна к погрешностям квантования, возникающим при округлении коэффициентов, поэтому выбрана именно она. Полученный фильтр порядка  N =12 можно реализовать как  каскадное соединение шести фильтров второго порядка [1, №26].

Каскадная форма представления передаточной функции данного фильтра имеет вид:

H(z) = H1(z)*H2(z)*H3(z)*H4(z)*H5(z)*H6(z)

Строки матрицы sos содержат коэффициенты фильтров второго порядка.

sos = tf2sos(numd, dend) ;

   0.96501497924877  -1.13149559117331   0.97002624640667   1.00000000000000   -1.15473570409626   0.98186894730068

   1.00000000000000  -1.18185876135643   1.00737356518320   1.00000000000000   -1.17513096897162   0.98204171987366

   1.00000000000000  -1.17861458988832   0.99478620935519   1.00000000000000  -1.18365022582988   0.99517047400962

   1.00000000000000  -1.16931196264285   0.99268410536002   1.00000000000000  -1.16172257419756   0.99519417036575

   1.00000000000000  -1.16628731799650   0.99786088974624   1.00000000000000   -1.16534494533725   0.99893526560938

   1.00000000000000  -1.18492878535466   1.00218798962479   1.00000000000000   -1.18458798425674   0.99897298107667

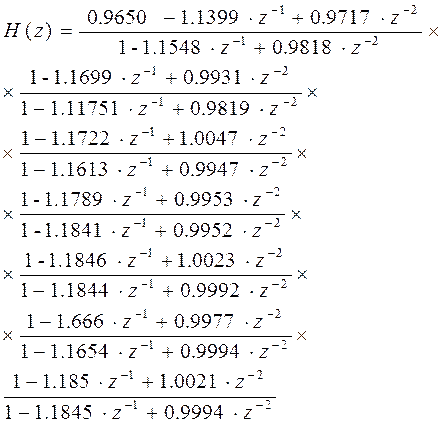
% построение АЧХ фильтра в каскадной форме

[numc, denc]=sos2tf(sos);

[Hc, fc]=freqz(numc, denc, 4096, Ft);

figure(5)

plot(f, abs(H), fc,abs(Hc))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

legend('АЧХ исходного фильтра', 'АЧХ фильтра в каскадной форме')

grid;

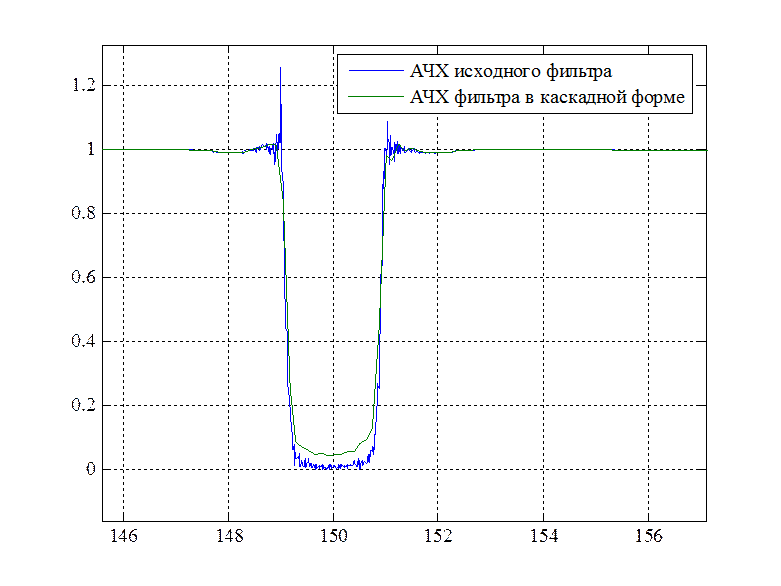
Рис. 6. АЧХ спроектированного фильтра и его каскадной формы

По графику видно, что АЧХ спроектированного фильтра и его каскадной формы близки друг к другу, следовательно, такая реализация фильтра допустима. Каскадная реализация необходима для возможности физического создания фильтра. Она, как было сказано ранее, более устойчива к ошибкам квантования и погрешностям округления по сравнению с прямой формой [1, №27].

5. Тестирование  фильтра

Для проверки работоспособности фильтра подадим на его вход сигнал, состоящий из суммы двух гармоник. Частота одной из них находится в полосе задерживания фильтра, а частота другой – в полосе пропускания.

n = 0:100;

y1 =cos(2*pi*150*(1/Ft)*n); %150 Гц (в полосе задерживания)

y2=cos(2*pi*70*(1/Ft)*n); %70 Гц (в полосе пропускания)

x=y1+y2;

5.1. Запись коэффициентов передаточных функций отдельных каскадов

n1=[ 0.96501497924877  -1.13149559117331   0.97002624640667   ];

d1=[1.00000000000000   -1.15473570409626   0.98186894730068];

n2=[1.00000000000000  -1.18185876135643   1.00737356518320   ];

d2=[1.00000000000000   -1.17513096897162   0.98204171987366];

n3=[1.00000000000000  -1.17861458988832   0.99478620935519   ];

d3=[1.00000000000000  -1.18365022582988   0.99517047400962];

n4=[1.00000000000000  -1.16931196264285   0.99268410536002   ];

d4=[1.00000000000000  -1.16172257419756   0.99519417036575];

n5=[1.00000000000000  -1.16628731799650   0.99786088974624   ];

d5=[1.00000000000000   -1.16534494533725   0.99893526560938];

n6=[1.00000000000000  -1.18492878535466   1.00218798962479];

d6=[1.00000000000000   -1.18458798425674   0.99897298107667];

5.2. Фильтрация суммы сигналов из полосы пропускания и полосы задерживания

F1=filter(n1,d1,x);

F2=filter(n2,d2,F1);

F3=filter(n3,d3,F2);

F4=filter(n4,d4,F3);

F5=filter(n5,d5,F4);

F6=filter(n6,d6,F5);

figure(5)

subplot(4,1,1), plot(n,y1),

set(gca,'FontName','Times New Roman Cyr','FontSize',12),

title('Гармоника 50 Гц');

subplot(4,1,2), plot(n,y2),

set(gca,'FontName','Times New Roman Cyr','FontSize',12),

title('Гармоника 70 Гц');

subplot(4,1,3), plot(n,x),

set(gca,'FontName','Times New Roman Cyr','FontSize',12),

title('Сигнал суммы гармоник');

subplot(4,1,4), plot(n,F6),

set(gca,'FontName','Times New Roman Cyr','FontSize',12),

title('Сигнал на выходе фильтра');

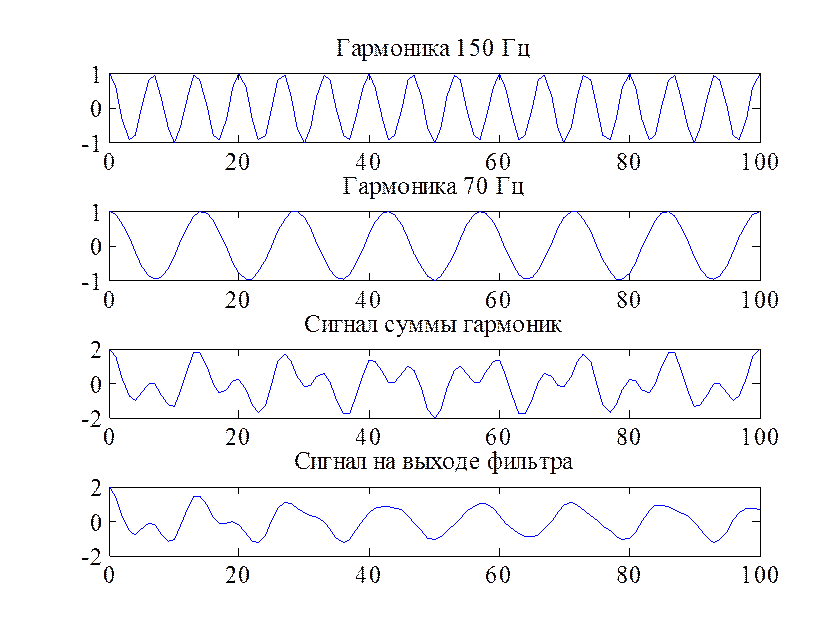
Рис.7. Сигналы двух гармоник, их суммы и выходной сигнал

По графику видно, что фильтр пропускает только гармонику с частотой, лежащей в полосе пропускания, и подавляет гармонику с частотой из полосы задерживания. Количественные оценки фильтрации сигналов приведены ниже.

5.3. Фильтрация сигнала частотой из  полосы задерживания

y2 =cos(2*pi*150*(1/Ft)*n); % 50 Гц (в полосе задерживания)

F1=filter(n1,d1,y2);

F2=filter(n2,d2,F1);

Скачать файл