Информатика и выч. техника \ Теория и обработка сигналов

Разработка цифрового режекторного эллиптического (Чебышева-Кауэра) БИХ-фильтра, страница 4

F3=filter(n3,d3,F2);

F4=filter(n4,d4,F3);

F5=filter(n5,d5,F4);

F6=filter(n6,d6,F5);

figure(6)

subplot(2,1,1), plot(n,y2),

set(gca,'FontName','Times New Roman Cyr','FontSize',12),

title('Гармоника 50 Гц');

subplot(2,1,2), plot(n,F6),

set(gca,'FontName','Times New Roman Cyr','FontSize',12),

title('Сигнал на выходе фильтра');

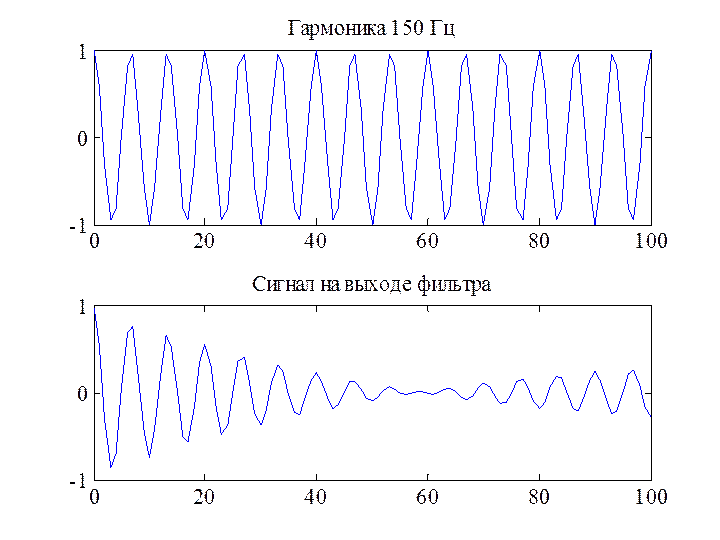
Рис.8. Сигнал с частотой 150Гц и сигнал на выходе фильтра

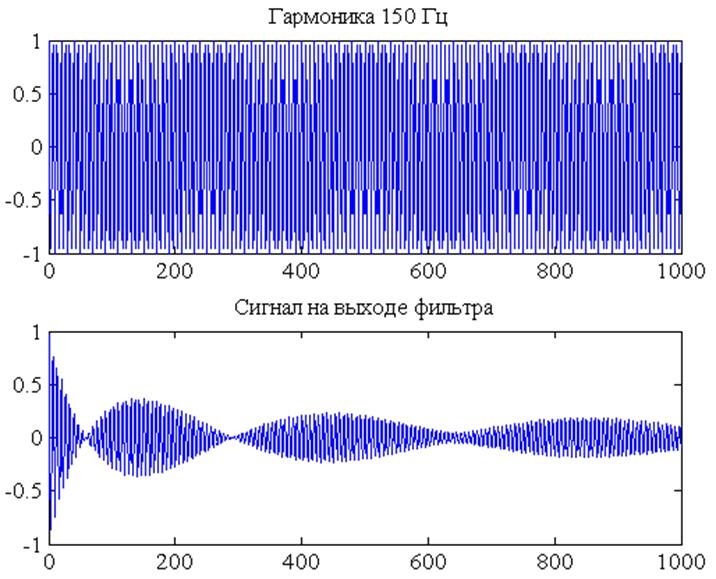
Рис.9. Сигнал с частотой 150Гц и сигнал

на выходе фильтра (увеличенный масштаб)

По графику видно, что фильтр ослабляет сигнал из полосы задерживания. Ослабление сигнала удовлетворяет заданным требованиям:

20*log10((y2)/(F6))= -73.64039560903301 Дб

5.4. Фильтрация сигнала частотой из  полосы пропускания

y3 =cos(2*pi*70*(1/Ft)*n); % 70 Гц (в полосе пропускания)

F1=filter(n1,d1,y3);

F2=filter(n2,d2,F1);

F3=filter(n3,d3,F2);

F4=filter(n4,d4,F3);

F5=filter(n5,d5,F4);

F6=filter(n6,d6,F5);

figure(7)

subplot(2,1,1), plot(n,y3),

set(gca,'FontName','Times New Roman Cyr','FontSize',12),

title('Гармоника 70 Гц');

subplot(2,1,2), plot(n,F6),

set(gca,'FontName','Times New Roman Cyr','FontSize',12),

title('Сигнал на выходе фильтра');

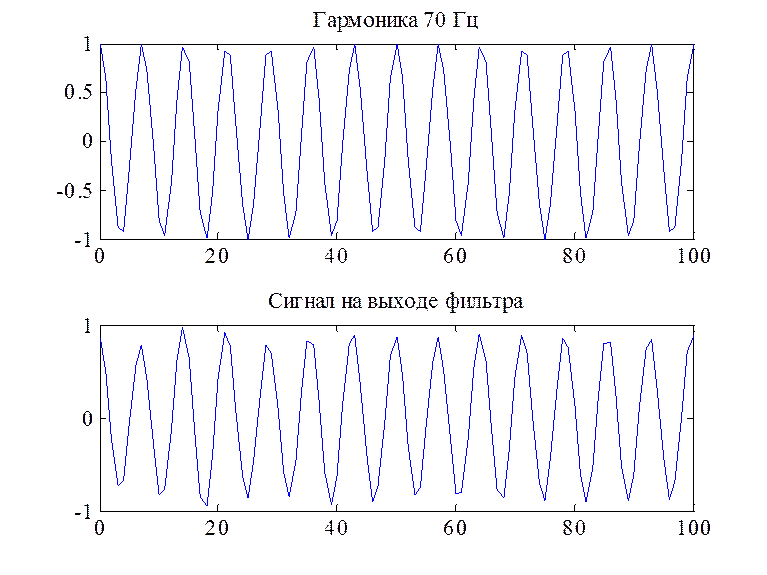
Рис.10. Сигнал с частотой 70Гц и сигнал на выходе фильтра

По графику видно, что сигнал с частотой из полосы пропускания проходит полностью лишь с ослаблением в пределах допустимого:

20*log10(max(y3)/max(F6)) = 0.03971813396194 Дб

6. Программирование фильтра и оценка быстродействия

Для программирования фильтра и анализа его быстродействия полученного фильтра используется программа на языке С++, позволяющая определить время, за которое программный фильтр обрабатывает входной сигнал с заданным количеством отсчетов.

Код программы тестирования фильтра :

#include <stdio.h>

#include <iostream.h>

#include <math.h>

#include <windows.h>

#include <conio.h>

#define N 100000

int por=2, Fd=500;          // порядок фильтров для каскадной формы и частота отсчетов

double b,B,a,A,

y[100000],                              // массив для формирования отсчетов выходного сигнала

x[100000],                              // массив для формирования отсчетов входного сигнала

F1[100000],           // массивы передачи сигнала между элементами   каскадной формы фильтра

F2[100000], F3[100000], F4[100000],  F5[100000], F6[100000];

double                          //коэф-ты полиномов числителя и знаменателя :

n1[3]={0.85432024970523,  -1.39165963991533,   0.86510055898402},

d1[3]={1.00000000000000,  -1.56929016354379,   0.96460591251597},

n2[3]={1.00000000000000,  -1.63535353521533,   1.01074516667436},

d2[3]={1.00000000000000,  -1.61713397214427,   0.96646927819649},

n3[3]={1.00000000000000,  -1.60831824766117,   0.98936049739017},

d3[3]={1.00000000000000,  -1.60279010156957,   0.99450138797575},

n4[3]={1.00000000000000,  -1.61465680040524,   0.98758101655097},

d4[3]={1.00000000000000,  -1.63170546722370,   0.99468540627541},

n5[3]={1.00000000000000,  -1.61536620169288,   1.00181177768894},

d5[3]={1.00000000000000,  -1.60934397796041,   0.99841911109092},

n6[3]={1.00000000000000,  -1.62808518506543,   0.99815733390805},

d6[3]={1.00000000000000,  -1.63135243556073,   0.99858549110240};

double Chebishev(double x[],int n, double m1[],double m2[])     // функция расчета выходного //сигнала

{

            for(int i=0;i<por+1;i++)

{

                    b=m1[i]*x[n-i];

                    B=b+B;

}

for(int i=1;i<por+1;i++)        

{

                    a=m2[i]*y[n-i];

                    A=a+A;         

}

           y[n]=B-A;

return y[n];  

}

DWORD WINAPI Thread_filter(LPVOID)                // поток для фильтрации сигнала

{  

double Chebishev(double x[],int n,double m1[],double m2[]);

double count,total;

count = GetTickCount();                                    // счетчик времени

for(int n=0;n<N;n++)                                // фильтрация входного сигнала

{

 F1[n]=Chebishev(x,n,n1,d1);

             F2[n]=Chebishev(F1,n,n2,d2);

             F3[n]=Chebishev(F2,n,n3,d3);

             F4[n]=Chebishev(F3,n,n4,d4);       

             F5[n]=Chebishev(F4,n,n5,d5);

             F6[n]=Chebishev(F5,n,n6,d6); }

 total = GetTickCount() - count;     // вычисление времени фильтрации входного  //сигнала

 cout<<"Time : ";

 cout<<total<<" ms"<<endl;

 return 0;

}

void main() 

{

unsigned long ThreadId;

for(int j=0;j<N;j++)   

{

     x[j]=2*cos((2*M_PI*150*j)*1/Fd)+cos((2*M_PI*70*j)*1/Fd);     // входной сигнал

}

CreateThread(NULL,0,Thread_filter,x,0,&ThreadId); //  запуск потока фильтрации  //сигнала

getch();

}

На компьютере с процессором Intel Core 2 Duo тактовой частотой 2.40 ГГц время фильтрации входного сигнала, являющегося суммой гармоник частотой 150 и 70 Гц при количестве отсчетов N=100000 составило 797мс =  0.797 секунды, следовательно, один отсчет выполняется за 7.9 мкс.

Максимальная частота, с которой способен работать цифровой фильтр, обратно пропорциональна  времени обработки одного отсчета, т.е. fmax= 126,5 КГц.

Заключение

            В результате курсовой работы был спроектирован режекторный эллиптический БИХ-фильтр (Чебышева-Кауэра), удовлетворяющий требованиям задания. При проектировании применялся метод аналогового прототипа, а переход к цифровому фильтру был осуществлен с помощью метода билинейного преобразования. Реализация полученного фильтра выполнена в форме последовательного соединения шести каскадов 2-го порядка. Тестирование фильтра показало его работоспособность: он отфильтровывает сигналы с частотами из полосы задерживания и пропускает сигналы с частотами из полосы пропускания. Быстродействие фильтра составляет 7.9 мкс на отсчет, что даёт предельную рабочую частоту 126,5 КГц.

Список используемой литературы

1.  Конспект лекций по дисциплине «Теория и обработка сигналов», семестр 6 (2009-2010 учебный год), автор доц. Щетинин Ю.И.

2.  Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов: Учеб. пособие. – Новосибирск. Изд-во НГТУ, 1998. – Ч.2. – 115  с.

3.  Голышев Н.В., Щетинин Ю.И. Задачник – практикум по теории и обработке сигналов: Учебное пособие – Новосибирск. Изд-во НГТУ,  2001. – Ч.2. – 80  с.

Скачать файл