Информатика и выч. техника \ Теория и обработка сигналов

Разработка цифрового режекторного эллиптического (Чебышева-Кауэра) БИХ-фильтра, страница 2

1. На основе спецификаций исходного проектируемого ЦФ выбирается подходящая аппроксимация для АЧХ: аппроксимация Баттерворта или Чебышева или эллиптическими функциями.

2. С помощью преобразования 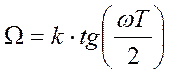определяются граничные (критические) частоты аналогового фильтра.

3. Для РФ вычисляются четыре граничные частоты

, , , .

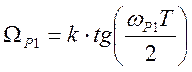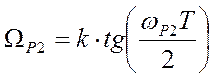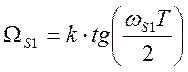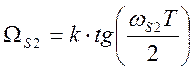4. Проектируется аналоговый нормированный ФНЧ. Определяется порядок и передаточная функция НФНЧ. [1, № 26].

Переход от полученного аналогового прототипа фильтра к цифровому может осуществляться различными методами:

· методом инвариантного преобразования импульсной характеристики аналогового фильтра в цифровой,

· билинейным преобразованием,

· методом дискретизации на основе дискретизации дифференциального уравнения аналогового фильтра соответствующим линейным разностным уравнением,

· методом согласованного z – преобразования. [1, №25]

В данной работе применяется метод, основанный на использовании аналогового прототипа, а переход к цифровому фильтру осуществляется на основе метода билинейного преобразования. Этот метод преобразования аналогового фильтра в цифровой применяется наиболее часто ввиду его простоты и качеств результирующих характеристик фильтров.

Метод билинейного преобразования:

Передаточная функция W(p) «р-плоскости» преобразуется в передаточную функцию W(z) «z-плоскости» цифрового БИХ-фильтра с помощью функции:

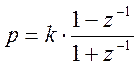где k–положительная константа.

Ось частот Ω в аналоговом случае преобразуется в единичную окружность так, что 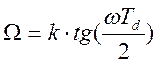и поэтому частота среза Ωс АЧХ аналогового фильтра будет соответствовать частоте среза АЧХ цифрового фильтра.

Устойчивость полученного таким образом цифрового фильтра гарантируется, если исходный аналоговый фильтр был устойчив и область устойчивости в одной комплексной плоскости путем преобразования отображается в область устойчивости в другой комплексной плоскости. Достоинством метода билинейного преобразования является то, что передаточная функция цифрового фильтра определяется с помощью простых формул из передаточной функции аналогового фильтра, для которых существуют подробные таблицы и справочники. Также метод билинейного преобразования по сравнению с другими методами преобразования аналоговых фильтров в цифровые (инвариантности импульсной характеристики и согласованного z-преобразования) обеспечивает построение такого БИХ-фильтра, выходной, сигнал которого приближенно совпадает с выходным сигналом аналогового фильтра-прототипа при произвольных одинаковых входных сигналах. Метод билинейного преобразования имеет и свои недостатки, наиболее значимым из которых является несоответствие импульсной и фазовой характеристик аналогового и цифрового фильтра. [2]

Проектирование фильтра

· Нижняя граничная частота полосы пропускания (Fpass1) -148 Гц,

· Верхняя граничная частота полосы пропускания (Fpass2) – 152 Гц,

· Нижняя граничная частота полосы задерживания (Fstop1) – 149 Гц,

· Верхняя граничная частота полосы задерживания (Fstop2) – 151 Гц,

· Неравномерность передачи в полосе пропускания (Apass) – 0,1 дБ,

· Минимальное ослабление в полосе задерживания (Astop)– 70 дБ,

Fpass1=148;

Fpass2=152;

Fstop1=149;

Fstop2=151;

Astop=70;

Apass=0,1;

Ft=1000;

3.1. Определение нормированных частот

wp1=2*pi*Fpass1/Ft;

wp2=2*pi*Fpass2/Ft;

ws1=2*pi*Fstop1/Ft;

ws2=2*pi*Fstop2/Ft;

нормировочные частоты:

wp1 = 0.9299

wp2 = 0.9550

ws1 = 0.9362

ws2 = 0.9488

3.2. Нахождение граничных частот фильтра

С помощью выражения 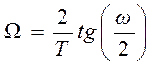найдем граничные частоты аналогового фильтра

Ws1=2*Ft*tan(ws1/2);

Ws2=2*Ft*tan(ws2/2);

Wp1=2*Ft*tan(wp1/2);

Wp2=2*Ft*tan(wp2/2);

Ws1 = 1.0111e+003

Ws2 = 1.0270e+003

Wp1 = 1.0033e+003

Wp2 = 1.0349e+003

3.3. Проверка условия геометрической симметрии, что требует данный метод

Wp1*Wp2= 1.0383e+006

Ws1*Ws2= 1.0384e+006

Это условие для метода проектирования билинейным преобразованием является обязательным.

Поскольку Ws1*Ws2 ≠ Wp1*Wp2, то скорректируем частоту

Wp2=Ws1*Ws2/Wp1= 1.0350e+003

3.4. Определение ширины полосы задерживания

Bw=Ws2-Ws1 = 15.8289

и центральной частоты полосы пропускания режекторного фильтра [1, №26]

Wo=sqrt(Ws1*Ws2) = 1.0190e+003

3.5. Расчет нормированного фильтра нижних частот (НФНЧ).
3.5.1. Нахождение граничной частоты полосы задерживания нормированного фильтра

Omega_s = (Wp2-Wp1)/(Ws2-Ws1) = 2.0070

3.5.2. Определение порядка и передаточной функции НФНЧ

[n,Wn]=ellipord(1,Omega_s, Apass, Astop,'s');

В данном случае N = 6 Wn = 1

[numd,dend]=ellip(n, Apass, Astop,Wn,'s'); % Расчет перед. функции НФНЧ

Функция ellip производит синтез дискретного эллиптического фильтра Чебышева первого рода n-го порядка, имеющего АЧХ фильтра нижних частот, нормированную частоту среза Wn, и обеспечивающего подавление сигнала в полосе задерживания, равное Astop дБ; Функция ellipord определяет минимальный порядок фильтра. ellip возвращает описание фильтра в виде векторов-строк num и den, имеющих длину n+1 и содержащих коэффициенты полиномов числителя и знаменателя передаточной функции в порядке убывания степеней переменной z: 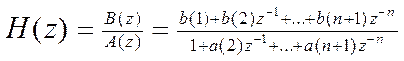[3, стр.79]

numd = 0.0003 0.0000 0.0160 0.0000 0.1288 0.0000 0.2671

dend = 1.0000 1.6983 3.0109 2.8718 2.2082 1.0359 0.2702

% построение АЧХ и ЛАЧХ аналогового НФНЧ:

[H, W] = freqs(num, den);

figure(1)

subplot(2,1,1);

plot (W, abs(H))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('График АЧХ аналогового НФНЧ');

subplot(2,1,2);

plot (W, 20*log10(abs(H)))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('График ЛАЧХ аналогового НФНЧ');

xlabel('w, рад');

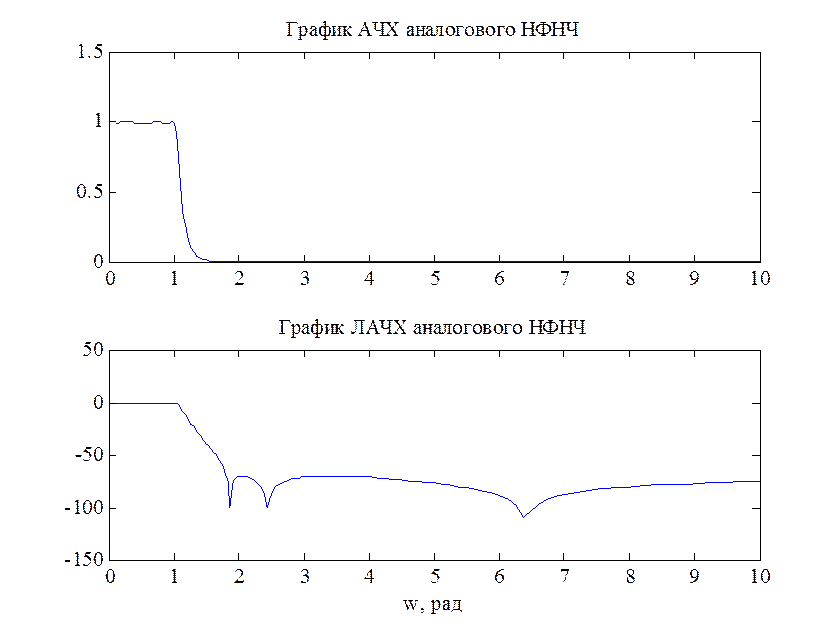
Рис.2. Графики АЧХ и ЛАЧХ аналогового НФНЧ

3.6. Трансформирование НФНЧ в аналоговый режекторный фильтр

[num, den]=lp2bs(numd,dend, Wo, Bw);

Переход от НФНЧ к РФ осуществляется на основе замены в передаточной функции вида:

1 2 3 4

Скачать файл