НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов», 5 - й семестр
ЛАБОРАТОРНАЯ РАБОТА № 1
НЕПРЕРЫВНЫЕ И ДИСКРЕТНЫЕ
ПО ВРЕМЕНИ СИГНАЛЫ
Цель работы:Знакомство со средой MATLAB, приобретение практических навыков генерирования непрерывных и дискретных по времени сигналов, построения графиков сигналов в среде MATLAB.
Задание и порядок выполнения работы
1.
Запустите MATLAB
на Вашей рабочей станции. После запуска
на экране появляется командное окно – CommandWindowMATLAB, предназначенное
для ввода команд и вывода результатов вычислений. В верхней части командного
окна расположена строка меню, под ним размещена панель инструментов с кнопками
- пиктограммами для выполнения некоторых наиболее часто используемых операций.
Главным средством для получения справочной информации в системе является
браузер справочной системы (Helpbrowser),
который обеспечивает пользователей документацией по всем инсталлированным
продуктам MATLAB. Для открытия браузера можно использовать команду
меню Help>Product Help, кнопку Help ![]() панели
инструментовили команду helpbrowser из командной строки.
панели
инструментовили команду helpbrowser из командной строки.
Справка MATLAB в
первую очередь предназначена для оперативного уточнения синтаксиса используемых
функций, их параметров и опций.
При известном имени команды для получения о ней справочных сведений достаточно ввести
>>
help <имя команды>.
Например,
>> help plot
для вывода справки о команде plot.
Более
детальные сведения можно получить с помощью команды >> doc <имя команды>.
При изучении MATLAB и создании приложений полезны также разнообразные
демонстрационные примеры, имеющиеся в справочной системе.
Доступ к
демонстрационным примерам можно получить из меню Help c помощью команды Demosили команды demo из командной строки. Демонстрации
систематизированы по разделам. Начинающим пользователям интересен раздел MATLAB с соответствующими демонстрационными
примерами.
Изучите
справочные сведения по следующим функциям и командам, наиболее часто используемым
при работе с графиками в MATLAB:
plot, stem, grid, subplot, figure, title, axis, xlabel, ylabel, legend.
2. Постройте график непрерывного по времени гармонического сигнала с
помощью следующей последовательности команд
A=10;
f=50;
phi=pi/5;
t=0:0.0005:0.04;
y=A*sin(2*pi*f*t-pi/5);
plot(t,y,'ro-')
grid
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('График гармоники')
xlabel('t, c')
ylabel('y(t)')
Ознакомьтесь с синтаксисом использованных здесь команд. Определите также амплитуду, мощность, среднеквадратичное значение, частоту, период и начальную фазу гармоники.
Указание. Рекомендуется составлять отчет по лабораторной
работе по мере выполнения отдельных её этапов (заданий). Для составления
отчета должна использоваться среда MS WORD.
Требования к отчету приведены в п.12. При выполнении отчета следует
пользоваться рекомендациями к оформлению отчетов, изложенными в одноименном
файле.
Пояснение. Свойства графиков (метки, заголовки, тип, ширину, цвет
линий и др.) можно настраивать также непосредственно в окне графики,
используя кнопку EditPlot
инструментальной панели окна, выделяя
затем мышью нужный объект и вызывая левой кнопкой соответствующее окно
свойств или правой кнопкой контекстное меню команд объекта.
Для получения начального навыка отредактируйте ширину и цвет линии графика.
3. Постройте график дискретного по времени гармонического сигнала с помощью последовательности команд
A=10;
f=50;
phi=pi/5;
n=0:1:40; % Номер отсчета
Fs=1000; % Частота отсчетов
y=A*sin(2*pi*f*n/Fs-pi/5);
figure
stem(n,y,'ro-')
grid
Введите заголовок «График
дискретной гармоники», а также метку ‘n’ по оси абсцисс и метку ‘y[n]’ по оси ординат. Сопоставьте графики п.2 и п.3.
Сформулируйте определения непрерывного и дискретного по времени сигнала и
объясните различия между ними.
4. Составьте и выполните последовательность команд для вычисления значений и построения графика нескольких (трех – пяти) периодов дискретной по времени гармоники с частотой 10 Гц, частотой отсчетов 100 Гц и начальной фазой π/2. Введите необходимые метки и заголовки.
5.
Используя команду hold, постройте
в одном графическом окне графики функций:
а) ![]() ,
,
б) ![]() ,
,
в)
![]() .
.
Выведите метки (legend) функций графика. Обратите внимание, что в подпункте
в) используется параметрическое задание функции y(x).
6. На интервале
![]() вычислите вектор значений комплексной
экспоненты (гармоники)
вычислите вектор значений комплексной
экспоненты (гармоники) ![]() с показателем
затухания σ = - 0, 0693 и периодом Т = 2 секунды. Постройте в отдельном
графическом окне график y с
помощью команды plot(y).
с показателем
затухания σ = - 0, 0693 и периодом Т = 2 секунды. Постройте в отдельном
графическом окне график y с
помощью команды plot(y).
В другом
графическом окне с четырьмя подокнами (команда subplot) постройте
графики действительной, мнимой части, модуля и аргумента y в зависимости
от t. Введите необходимые метки и заголовки графиков.
Сопоставьте и объясните полученные результаты.
7. В соответствии с вариантом индивидуального задания (Приложение 1) проведите вычисление значений заданного сигнала и постройте его график с выводом заголовка и меток по осям. Предварительно по справочной системе ознакомьтесь с синтаксисом соответствующей функции и опишите его. Полезно также ознакомиться с функциями остальных вариантов задания.
8.
Познакомьтесь с созданием файл - функций (Matlabfunction) и script-файлов (Matlabscript) в среде MATLAB, используя электронное учебное пособие «Matlab в ТОС» или другие
учебные (справочные) материалы.
На основе метода прямоугольников для вычисления определенного
интеграла
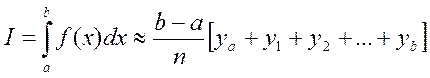 ,
,
напишите файл-функцию для
численного вычисления интеграла от функции ![]() на
интервале
на
интервале ![]() , основываясь на команде sum MATLAB без
использования цикла for. Синтаксис функции
, основываясь на команде sum MATLAB без
использования цикла for. Синтаксис функции ![]() ,
где N–
число точек (прямоугольников).
,
где N–
число точек (прямоугольников).
Для вычислениятого же интеграла напишите script
– файл (файл – сценарий), в котором предусмотрен ввод значений числа точек Nс помощью
команды input. Этот . m-файл может
содержать цикл for.
Обратите внимание, что файл – функция и скрипт - файл должны иметь комментарии для вывода пользователям необходимых справочных сведений.
Сформулируйте в отчете назначение и основные правила написания (составления) файл - функций и скрипт – файлов Matlab.
9. Составьте
файл-сценарий, в котором выполняется:
- генерирование 50 значений случайного шума с помощью функции randn(),
- генерирование сигнала ![]() ,
,
- построение графиков шума,
сигнала и их суммы (смеси) в отдельных графических подокнах с выводом метки оси
абсцисс и названий сигналов (команда legend).
Выполните этот файл – сценарий и кратко прокомментируйте результаты.
10. Изучите процедуру, представленную в Приложении 2. В ней показано генерирование часто используемых дискретных сигналов: единичного импульса, ступенчатого и пилообразного. Прокомментируйте в отчете операторы формирования каждого из этих сигналов. Выполните программу и представьте результаты в отчете.
11. Факультативное задание. Одной из важнейших традиционных областей
приложений обработки сигналов является обработка аудиосигналов. Звуком называют
звуковые ощущения, вызванные звуковыми (акустическими) колебаниями среды распространения.
Ухо человека слышит звуковые колебания в диапазоне частот от 16 до
20000 Гц. Характер звука определяется четырьмя основными свойствами: высотой,
громкостью, тембром и длительностью. Высота звука определяется частотой
колебаний. В Приложении 3 приведены данные по частотам, соответствующим
определенным нотам.
Амплитуда колебаний определяет громкость звука. При этом интенсивность акустической волны воспринимается ухом логарифмически, т.е. ощущение в два раза громче означает двукратное увеличение логарифма отношения амплитуд звукового сигнала, а не просто отношения амплитуд сигналов. Поэтому сила звука измеряется в логарифмах отношения амплитуд, чаще всего в децибелах.
Тембр звука зависит от наличия в нем кроме основного тона (основной частоты) "частичных" тонов или, иначе говоря, обертонов (гармоник). Длительность звука - это продолжительность колебаний источника звука.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.