В Приложении 4 приведена процедура, позволяющая сгенерировать и прослушать последовательность нот первой октавы. Часть звукоряда, в состав которой входят все семь основных ступеней (нот) До, Ре, Ми, Фа, Соль, Ля, Си, называется октавой. Каждая октава делится на 12 равных частей, называемых полутонами. Такой строй называют темперированным. Полутон является самым узким расстоянием между двумя соседними звуками музыкального звукоряда. Расстояние, образованное двумя полутонами, называется целым тоном.
Проанализируйте организацию процедуры и выполните её.
Напишите
файл – функцию с синтаксисом
[x, t] = harmonic(omega0, omegas, dur) для генерирования
синусоидального сигнала. Здесь omega0 - угловая частота гармоники, рад/с, omegas - угловая частота отсчетов, рад/с, dur
- продолжительность сигнала, c, x
– вектор значений сигнала, t
– вектор значений времени.
Используя эту функцию, сгенерируйте и постройте графики (первые 100
отсчетов) гармоник с частотами
omega0 = 2*pi*261,63 (нота До первой октавы) и omega0 = 2*pi*880 (нота Ля второй октавы) , omegas = 2*pi*8192 рад/с и длительностью dur= 1с.
С
помощью функции harmonic генерируйте
также и постройте график сигнала ![]() длительностью 1с.
длительностью 1с.
Ознакомьтесь с синтаксисом функции sound(), позволяющей с помощью звуковой карты компьютера
воспроизвести звуковой сигнал. Обратите внимание, что функция sound() и подобные ей по
назначению функции soundsc() и wavplay() применяют
интерполяцию для формирования сигналов непрерывного времени при
воспроизведении цифрового звука по отсчетам. Используя наушники или
звуковые колонки, прослушайте сгенерированные сигналы.
12. Проверьте усвоение материала по контрольным вопросам и упражнениям.
Окончательно оформите отчет по лабораторной работе. Отчет должен включать:
§ титульный лист,
§ название и цель работы,
§ формулировки пунктов работы в краткой общепринятой для научно – технических материалов форме,
§ команды и .m – файлы, графики, необходимые комментарии и пояснения, относящиеся к отдельным этапам работы и выводы по всей работе.
Литература
1. Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.: Уч. пособие.- Новосибирск. Изд-во НГТУ, 1998 - ч.1.
2. Щетинин Ю.И. MATLAB в ТОС: Электронное уч. пособие. - Новосибирск. 2004.
3. Теория и обработка сигналов. Методические указания к решению задач и упражнений по курсу / Составитель Щетинин Ю.И. - Новосибирск, Изд. НГТУ, 2007.
Web – ресурсы
1. http://www.mathworks.com/academia/student_center/tutorials/launchpad.html
(сайт компании MathWorks)
Контрольные вопросы и упражнения
1. Поясните различия непрерывных и дискретных по времени сигналов.
2. Объясните синтаксис и использование функции построения графиков plot() .
3.
Постройте график непрерывной по
аргументу функции
![]()
с выводом заголовка, меток по осям и сетки.
4.
Постройте график дискретного
сигнала
![]()
с выводом заголовка и меток по осям.
5. Объясните различия функций построения графиков plot() и stem().
6.
Постройте графики сигналов
а) ![]() ,
,
б) 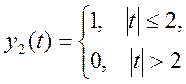
в отдельных подокнах одного графического окна.
7.
Покажите, что два аналоговых
сигнала
![]()
неразличимы при дискретизации с частотой Fs
= 40 Гц. Объясните причину данной особенности.
8.
Постройте график функции ![]() в виде столбчатой диаграммы (bar).
в виде столбчатой диаграммы (bar).
9. Используя функцию hist(), постройте график гистограммы случайной величины, формируемой встроенной функцией randn().
10. Пусть х = -3 : 7; n = [0 0 0 2 0 1 -1 3 0 0 0]. Постройте в одном графическом окне график сигнала x и графики задержанного (сдвинутого вправо) на два отсчета сигнала, а также сдвинутого вправо на один отсчет и зеркально повернутого относительно оси y сигнала.
11. Что такое файл-сценарий (script-файл) Matlab? Для чего используются файл – сценарии?
12. Объясните назначение и синтаксис файл - функции MATLAB. Напишите файл-функцию, которая суммирует элементы массива с четными индексами.
13. Напишите файл – функцию для вычисления значений
функции
![]() .
.
14. Постройте график функции ![]() ,
где обозначения соответствуют пункту 7 работы.
,
где обозначения соответствуют пункту 7 работы.
15. Объясните назначение и синтаксис функции sound().
Приложение 1
Таблица вариантов индивидуальных заданий
|
№ вар |
Вид сигнала (функции) |
Параметры |
||||
|
Интервал времени t, с |
Длительность w, с |
Частота f, Гц |
Частота отсчетов fS, Гц |
Вид функции func |
||
|
1 2 3 4 5 6 7 8 9 10 11 12 |
sawtooth square sinc rectpuls tripuls pulstran pulstran sawtooth sinc tripuls pulstran square |
0…0,1 0..1 -5…5 -5…5 -2…2 0…1 -1…1 -2…2 -10…10 -1…1 -2…2 0…2 |
3 1,6 1 0,1 0,5 0,05 60% |
50 100 4 2 2 5 5 |
10000 5000 20 20 1000 500 1000 5000 100 5000 1000 500 |
rectpuls tripuls rectpuls |
Приложение 2
% Процедура генерирования и построения графиков
% единичного импульса (imp), ступенчатого (step)
% и пилообразного (ramp) сигналов
L = input('Введите длину сигнала = ');
n = 1:L;
FT = input(' Введите частоту отсчетов = ');
T = 1/FT;
imp = [1 zeros(1,L-1)];
% вариант imp = (n==1);
step = ones(1,L);
ramp = (n-1).*step;
subplot(3,1,1);
stem(n-1,imp);
set(gca,'FontName','Arial Cyr', 'FontSize',10)
xlabel([' Интервал отсчетов',num2str(T), ' сек']);
ylabel('Амплитуда');
subplot(3,1,2);
stem(n-1,step);
set(gca,'FontName','Arial Cyr', 'FontSize',10)
xlabel(['Интервал отсчетов ',num2str(T), ' сек']);
ylabel('Амплитуда');
subplot(3,1,3);
stem(n-1,ramp);
set(gca,'FontName','Arial Cyr', 'FontSize',10)
xlabel(['Интервал отсчетов',num2str(T), ' сек']);
ylabel('Амплитуда');
|
Частота, Гц Hота |
Суб- контp- октава |
Контp- октава |
Большая октава |
Малая октава |
1 октава |
2 октава |
3 октава |
4 октава |
5 октава |
||
|
До До-диез Ре Ре-диез Ми Фа Фа-диез Соль Соль-диез Ля Си-бемоль Си |
C C# D D# E F F# G G# A B H |
20.61 21.82 23.12 24.50 25.95 27.50 29.13 30.87 |
32.70 34.65 36.95 38.88 41.21 43.65 46.25 49.00 51.90 55.00 58.26 61.74 |
65.41 69.30 73.91 77.78 82.41 87.31 92.50 98.00 103.80 110.00 116.54 123.48 |
130.82 138.59 147.83 155.56 164.81 174.62 185.00 196.00 207.00 220.00 233.08 246.96 |
261.63 277.18 293.66 311.13 329.63 349.23 369.99 392.00 415.30 440.00 466.16 493.88 |
523.25 554.36 587.32 622.26 659.26 698.46 739.98 784.00 830.60 880.00 932.32 987.75 |
1046.5 1108.7 1174.6 1244.5 1318.5 1396.9 1480.0 1568.0 1661.2 1720.0 1864.6 1975.5 |
2093.0 2217.4 2349.2 2489.0 2637.0 2793.8 2960.0 3136.0 3332.4 3440.0 3729.2 3951.0 |
4186.0 4434.8 4698.4 4978.0 5274.0 |
|
Приложение 4
% Процедура формирования и проигрывания последовательности нот
% Каждая последующая нота имеет частоту, большую в 21/12 раз, чем предыдущая
fs = 8192; % частота отсчетов
t = 0:1/fs:0.4; % длительность каждой ноты
tspace = .05; % длительность паузы между нотами
fr = 2^(1/12); % отношение частот соседних нот
A4 = 440; % Частота ноты ЛЯ первой октавы - опорная нота
B4 = A4*fr^2; % Частота ноты СИ первой октавы
C5 = A4*fr^3; % Частота ноты ДО второй октавы
C4 = A4*fr^(-9);
D4 = A4*fr^(-7);
E4 = A4*fr^(-5);
F4 = A4*fr^(-4);
G4 = A4*fr^(-2);
xspace = zeros(size(tspace));
% формирование вектора нот и пауз между ними
x = [cos(C4*2*pi*t),xspace, cos(D4*2*pi*t),xspace,cos(E4*2*pi*t),...
xspace,cos(F4*2*pi*t),xspace,cos(G4*2*pi*t),xspace,...
cos(A4*2*pi*t),xspace,cos(B4*2*pi*t),xspace,cos(C5*2*pi*t)];
sound(x,fs); % прослушивание вектора x
Составил доц. Щетинин Ю.И.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.