Задачи 9
Примеры решения задач
1. Определите
Z – преобразование и его
область сходимости для сигнала
![]()
Решение.
По выражению Z – преобразования
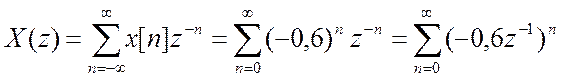 .
.
Полученное выражение представляет собой сумму бесконечной геометрической прогрессии, поэтому
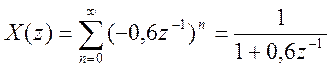
Область сходимости (ОС): ![]() , т.е.
, т.е. ![]() .
.
2. Определите
Z – преобразование и его
область сходимости для сигнала
![]()
Решение.
Найдем Z – преобразование x1[n] по выражению двустороннего Z – преобразования
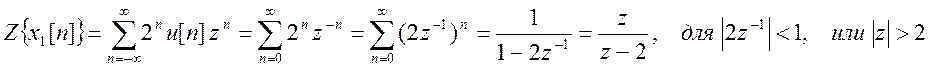 Теперь определим Z
– преобразование x2[n] .
Теперь определим Z
– преобразование x2[n] .
Для этого сигнала 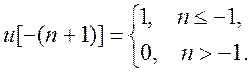
Пояснение: пусть 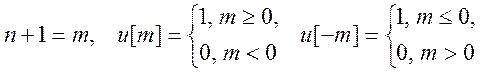
Если ![]() ,
то
,
то ![]() и
и ![]() .
.
Поскольку последовательность x2[n]
левосторонняя, т.е. определена для отрицательных значений n, то для нахождения
его Z – преобразование
используем формулу двустороннего Z –
преобразования
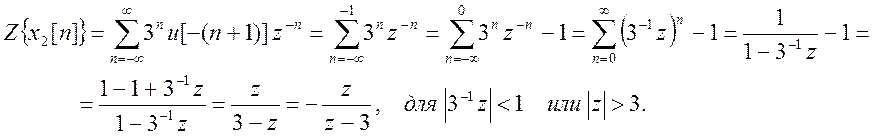
Z – преобразование всего сигнала
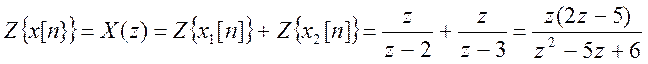 .
.
Область сходимости ![]() - это пересечение областей
сходимости преобразований
- это пересечение областей
сходимости преобразований ![]() и
и ![]() , т.е. кольцо
, т.е. кольцо ![]() .
.
3. Определите Z – преобразование сигнала
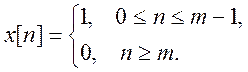
Решение.
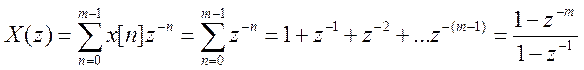
Область сходимости ![]() или
или
![]() .
.
4. Определите Z – преобразование и его область
сходимости для
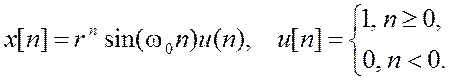 .
.
Решение.
С помощью формулы Эйлера представим
x[n] в виде 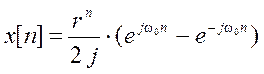 . Основываясь на известном Z-
преобразовании
. Основываясь на известном Z-
преобразовании 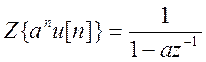 и используя свойство
линейности Z – преобразования, получаем
и используя свойство
линейности Z – преобразования, получаем
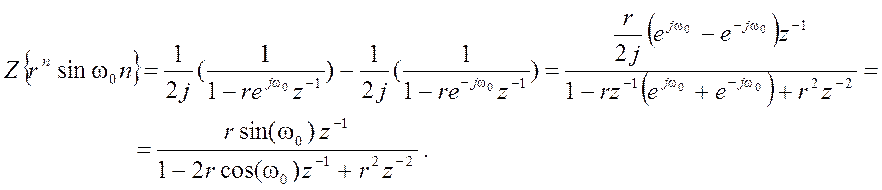
Полюса этого выражения ![]() . Поэтому область сходимости
. Поэтому область сходимости ![]() .
.
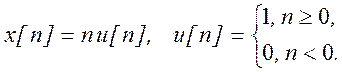
Решение.
Z- преобразование единичной
импульсной последовательности ![]()
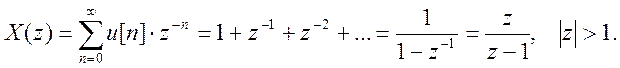 Полюс
X(z) – точка z=1.
Полюс
X(z) – точка z=1.
В соответствии со свойством дифференцирования Z- преобразования:
если 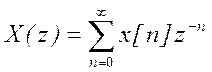 ,
то
,
то 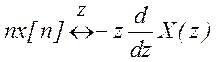 .
.
Поэтому 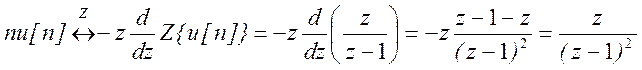 .
.
Таким образом, 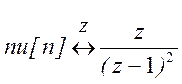 .
.
Запишем сигнал в виде ![]()
Z-изображение второго слагаемого 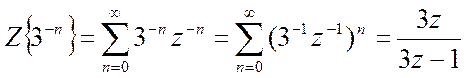 .
.
На основе теоремы (свойства) умножения на n
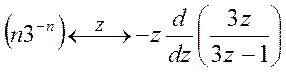 .
. 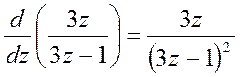
По свойству линейности 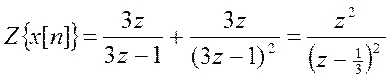 .
.
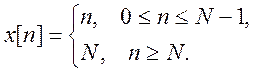
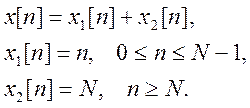
Для этого вначале вычислим преобразование для конечной последовательности
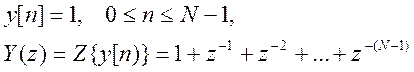
Это выражение представляет собой
сумму конечной геометрической прогрессии со знаменателем z-1. Согласно
формуле суммы конечной геометрической прогрессии 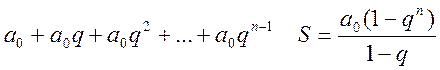 выражение
для Y(z) можно записать в виде
выражение
для Y(z) можно записать в виде 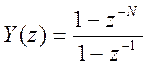 .
.
y[n] и x1[n]
связаны выражением ![]() . В соответствии со
свойством дифференцирования (умножения на n) Z
- преобразования
. В соответствии со
свойством дифференцирования (умножения на n) Z
- преобразования 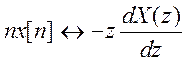 . Применим это свойство к x1[n].
. Применим это свойство к x1[n].
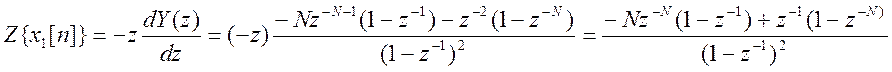 Теперь
запишем Z- преобразование для x2[n].
Эта последовательность представляет собой единичную последовательность,
умноженную на константу N и сдвинутую вправо на N отсчетов. Z- преобразование единичной последовательности равно
Теперь
запишем Z- преобразование для x2[n].
Эта последовательность представляет собой единичную последовательность,
умноженную на константу N и сдвинутую вправо на N отсчетов. Z- преобразование единичной последовательности равно
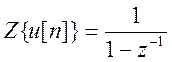 . Поэтому
. Поэтому 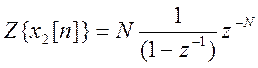 .
.
В результате Z- преобразование исходной последовательности
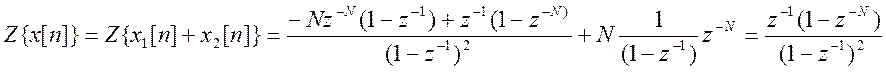
В соответствии с выражение Z - преобразования ![]()
последовательность x[n] должна иметь вид
![]()
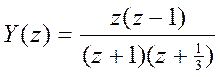 .
. Решение.
Будем определять обратное Z- преобразование методом разложения на простейшие дроби и нахождения оригинала для каждой составляющей разложения.
Y(z) - неправильная рациональная дробь.
Возьмем 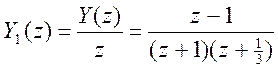 -
правильная дробь.
-
правильная дробь.
Разложим Y1(z) на простейшие дроби 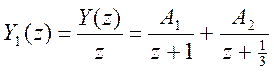
Определим константы разложения
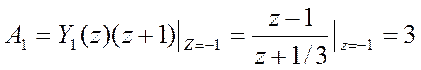 ,
,
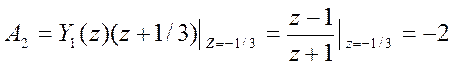 .
.
Переходя от Y1(z)
к Y(z), получим 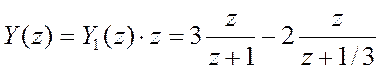 .
.
Используя соответствие между показательной функцией и её Z – изображением, получаем
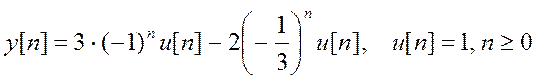 .
.
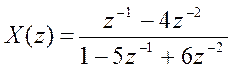 .
.Решение.
Запишем X(z) в
виде 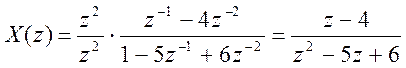
Найдем полюса X(z)
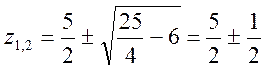 . Перейдем от X(z) к
. Перейдем от X(z) к 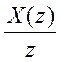 /Выразим в виде суммы простых
дробей
/Выразим в виде суммы простых
дробей 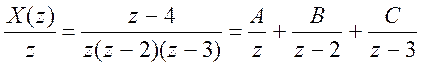 . Определим константы A, B, C.
. Определим константы A, B, C.
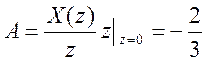 .
.
Аналогичными приемами найдем
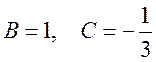 .
.
Следовательно, 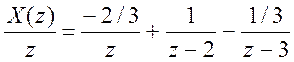 .
.
Отсюда
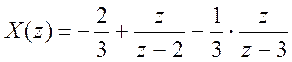 - представление в виде суммы
простейших дробей.
- представление в виде суммы
простейших дробей.
Вычисляя обратное Z – преобразование от каждой из дробей X(z), получаем
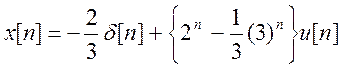 .
.
Решение.
В данном случае Z – преобразование не является рациональным, поэтому для инверсии нельзя применить методику разложения на простые дроби. Используем другой прием.
Найдем производную X(z)
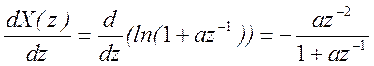 .
.
Согласно свойству дифференцирования Z – преобразования
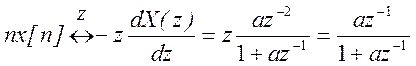 .
.
Обратное Z
– преобразование 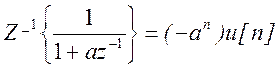 .
.
Выражение 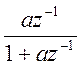 отличается
от
отличается
от 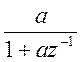 лишь множителем
лишь множителем ![]() . Согласно свойству запаздывания
(смещения) Z – преобразования
. Согласно свойству запаздывания
(смещения) Z – преобразования
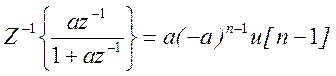 .
.
Следовательно, ![]()
И окончательный результат решения
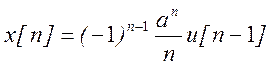 .
.
12.
Найдите сигнал по его Z – преобразованию
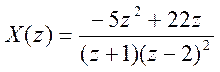 .
.
Решение.
Данное выражение X(z)
имеет 3 полюса: p1 = -1, p2
= 2 и p3 =2. Полюс p
= 2 – кратный с кратностью 2. Поэтому разложение X(z) на
простейшие дроби имеет вид
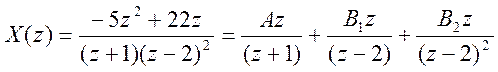 /
/
Найдем значения вычетов – коэффициентов разложения X(z):
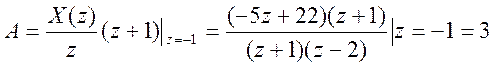
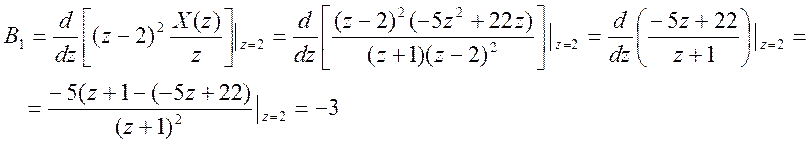
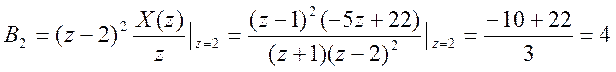
Таким образом, разложение на простейшие дроби для X(z) есть
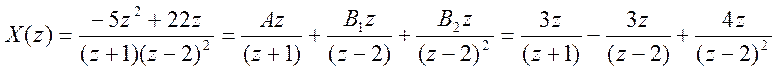
Этому выражению во временной области соответствует сигнал
![]() .
.
Пояснение:
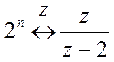
По свойству умножения на 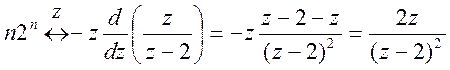
![]()
при ![]() и
с начальными условиями
и
с начальными условиями ![]() .
.
Решение. Запишем Z – преобразование от левой и правой части уравнения, используя свойство линейности и временного сдвига.
При этом
![]()
Z – преобразование
входного сигнала 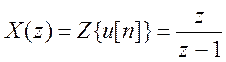 .
.
После подстановки X(z) и начальных
условий получим 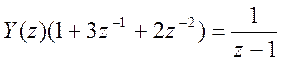 .
.
Следовательно, решение уравнения в Z – плоскости
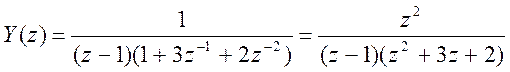
Полюса Y(z)
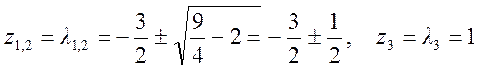
Разложение Y(z) на простые дроби 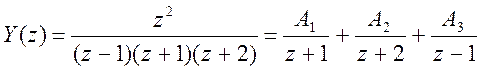
Найдем коэффициенты числителей дробей
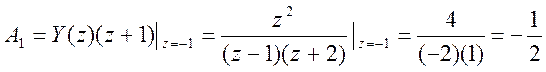
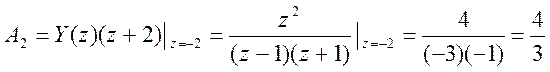
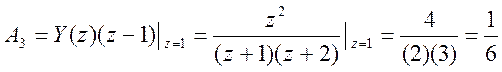 .
.
Следовательно,
![]()
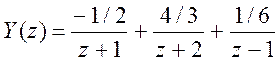 ,
или
,
или 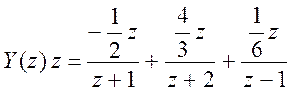 .
.
Обратное Z- преобразование от правой части
![]()
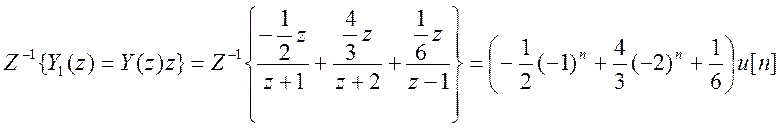 .
.
Связь между Y1(z)
и Y(z): ![]()
С учетом свойства временного сдвига Z – преобразования,
получаем решение уравнения во временной области в виде
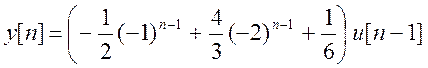
Решение.
Найдем Z – преобразование для x[k]:
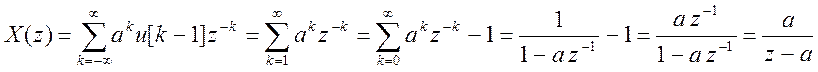
ДВПФ – это Z
– преобразование на единичной окружности, т.е. при ![]() .
.
Поэтому
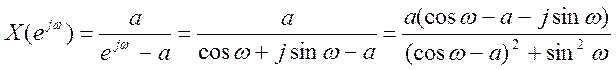 ,
,
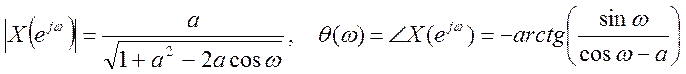 .
.
Графики сигнала, его амплитудного
и фазового спектров, т.е. модуля и аргумента ![]()
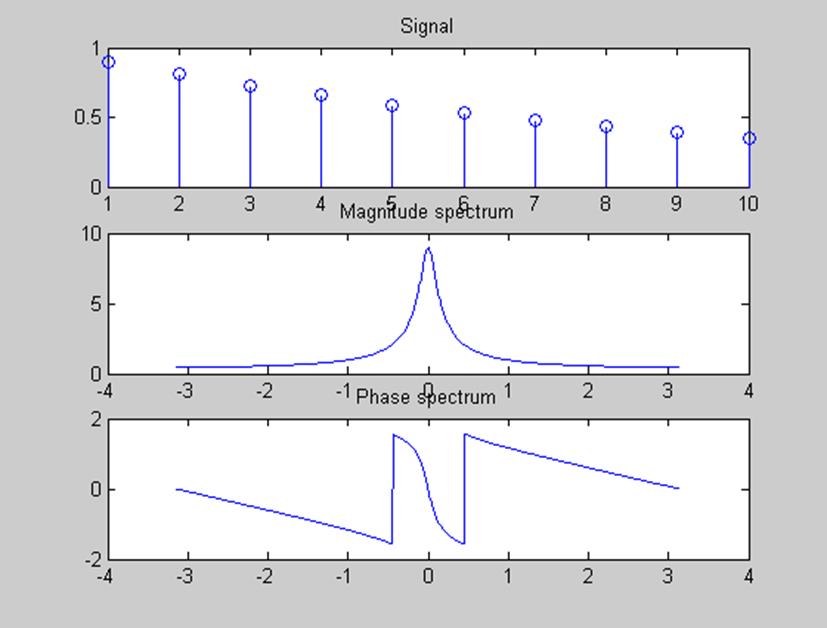
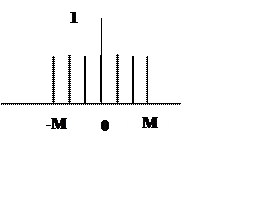
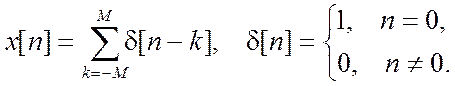 ,
,
Решение.
По формуле суммы конечной геометрической прогрессии
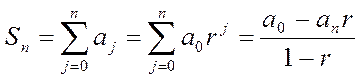 .
.
Поэтому
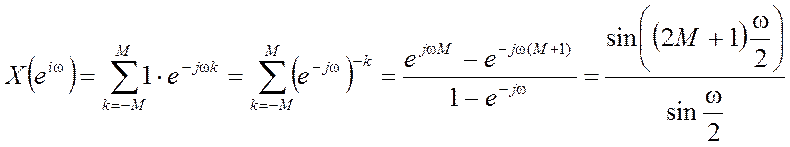
В последнем преобразовании
используется выделение множителя ![]() и формула Эйлера.
и формула Эйлера.
16. Определите ДВПФ для
сигнала ![]() .
.
Решение.
Запишем x[n] в виде ![]() .
.
ДВПФ сигнала ![]() есть
есть 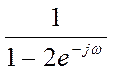 ,
т.к.
,
т.к. 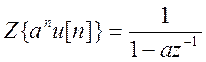 .
.
По свойству (теореме) сдвига ДВПФ
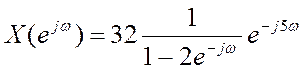 .
.
17. Найдите сигнал, ДВПФ которого имеет вид
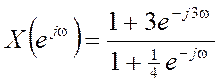 .
.
Решение.
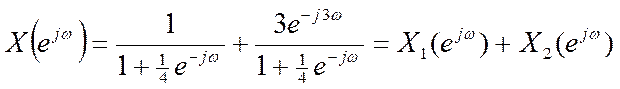
Обратные ДВПФ для членов X1(ejω) и X2(ejω)
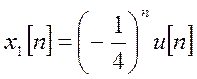 ,
, 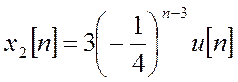 . Отсюда
. Отсюда 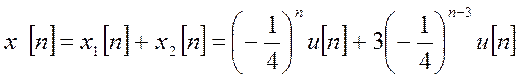 .
.
18. Пусть сигнал x[n] имеет ДВПФ в виде
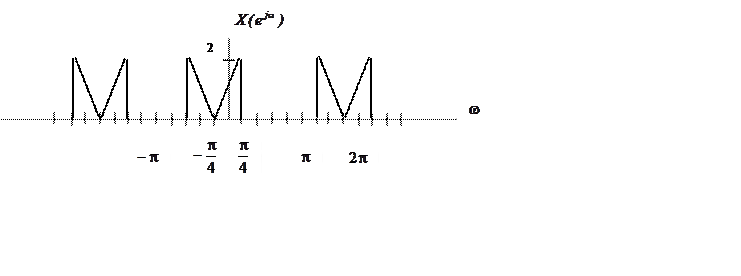 |
Определите: а)![]() , б)
, б) 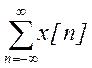 ,
в)
,
в)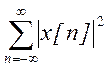 без явного вычисления
без явного вычисления ![]() .
.
Решение.
а) Из выражения обратного
ДВПВ 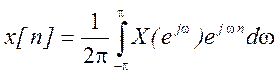 для n
= 0 получаем
для n
= 0 получаем
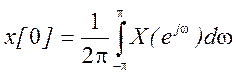 .
Интеграл
.
Интеграл 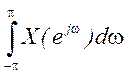 равен сумме площадей двух соответствующих
треугольников, т.е.
равен сумме площадей двух соответствующих
треугольников, т.е. 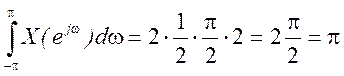 . Поэтому
. Поэтому 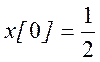 .
.
б) Выражение прямого ДВПФ 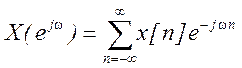 . Подставляя
. Подставляя ![]() , получаем
, получаем 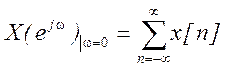 .
Поэтому из графического изображения
.
Поэтому из графического изображения ![]() имеем
имеем 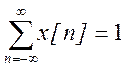 .
.
в) По теореме (равенству) Парсеваля для дискретных сигналов
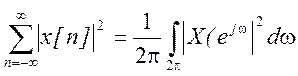 .
.
Из графического изображения ![]() , принимая во внимание геометрический
смысл определенного интеграла, получаем
, принимая во внимание геометрический
смысл определенного интеграла, получаем
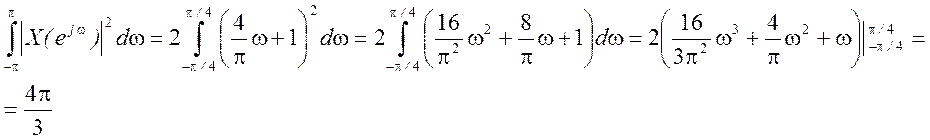 Следовательно,
Следовательно,
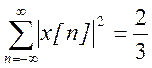 .
.
Задачи для самостоятельного решения
1. Найдите обратное (инверсное) Z – преобразование:
а) ![]()
Ответ: ![]()
б) 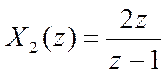
Ответ: x2[n]=2, n≥0.
в)
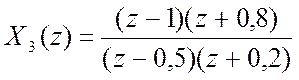 ,
,
Ответ: ![]() .
.
г) 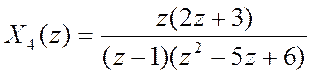 ,
,
Ответ: 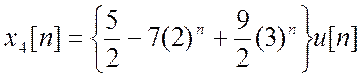 .
.
д) 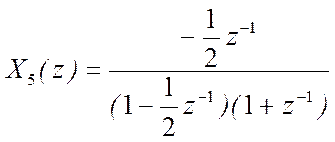
Ответ: 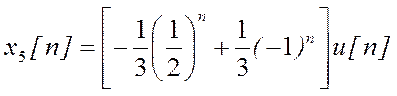 .
.
1. Определите
Z- преобразования для следующих сигналов:
а) ![]() - единичная ступенчатая функция.
- единичная ступенчатая функция.
Ответ:
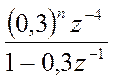 .
.
б)
![]() .
.
Ответ: 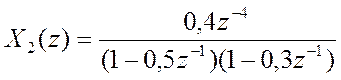 .
.
в)
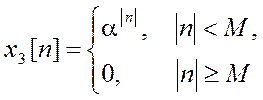
Ответ:
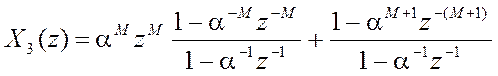
г)
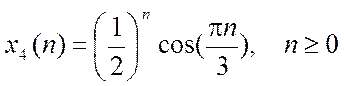 .
.
Ответ: 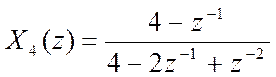 .
.
д)
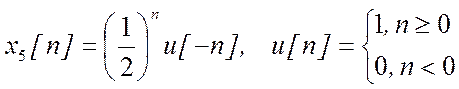 .
.
Ответ:
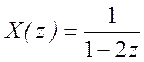 .
.
2. Определите
Z – преобразование и его
область сходимости для сигнала
![]() .
.
Ответ. 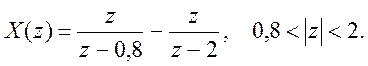
3. Определите
ДВПФ сигнала 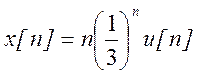 .
.
Ответ. 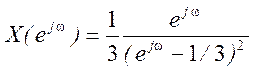 .
.
4.
Найдите ДВПФ, амплитудный и фазовый спектры сигнала ![]()
Ответ. 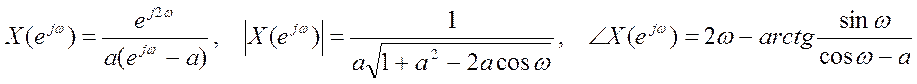
5. Определите ДВПФ сигналов и изобразите их амплитудные спектры
а) 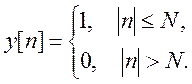
Ответ: 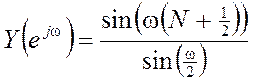 .
.
б ) ![]() ,
,
в) 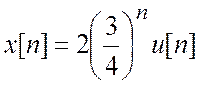 .
.
7. Докажите, что для действительной последовательности x[n] амплитудный спектр 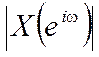 является четной функцией от ω,
а фазовый спектр
является четной функцией от ω,
а фазовый спектр ![]()
- нечетной функцией от ω.
8. Найдите вид сигнала x[n], ДВПФ которого
![]() .
.
Ответ. X[-4]=4, x[-1]=-1, x[0]=6, x[3]=8.
9. Решите разностное уравнение
![]() ,
здесь
,
здесь 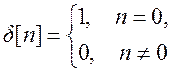
Начальные условия – нулевые.
Ответ. 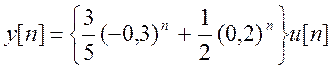 .
.
10. Решите
разностное уравнение
![]()
с начальными условиями ![]() .
.
Ответ. 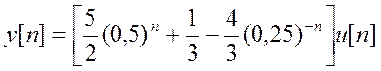
11. Изобразите графики нулей и полюсов для каждого из
следующих Z – преобразований
а) 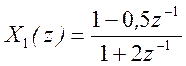 ,
,
б) 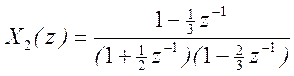 .
.
Составил: доц. Щетинин Ю.И.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.