
Определение
дискретно – временного преобразования Фурье
Преобразование Фурье непрерывного сигнала x(t)
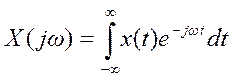
ставит в соответствие функции x(t) её спектральную плотность X(jω). Для сигналов дискретного аргумента x(nΔt)=x[n], Δt = 1/FS преобразование Фурье имеет некоторые особенности и свойства, обусловленные дискретизацией. Эту разновидность называют дискретно – временным преобразованием Фурье (ДВПФ).
Для его получения представим интеграл в виде приближения - интегральной суммы
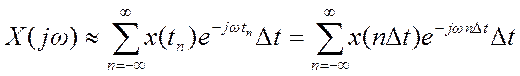 .
.
Для ![]()
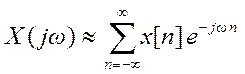 .
.
Правая часть получившегося выражения и есть дискретно – временное преобразование Фурье (англ. Discrete Time Fourier Transform, DTFT) дискретного сигнала x[n] , которое определяется следующим образом
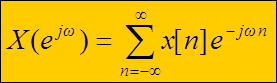 – прямое ДВПФ, выражение анализа.
– прямое ДВПФ, выражение анализа.
Оно имеет для дискретных сигналов x[n] тот же смысл, что обычное прямое преобразование Фурье
для непрерывных сигналов x(t).
Нотация ![]() .
.
В некоторых источниках его
обозначают как X(ω). В данном курсе используется
нотация ![]() .
.
ДВПФ позволяет найти частотный
спектр ![]() , называемый также спектром Фурье,
последовательности x[n].
, называемый также спектром Фурье,
последовательности x[n].
В общем случае X(e jω) – комплексная функция действительной переменной ω и может быть представлена в алгебраической или в полярной (показательной) форме
![]() .
.
В этих выражениях
![]() - действительная часть,
- действительная часть, ![]() - мнимая часть ДВПФ сигнала x[n],
- мнимая часть ДВПФ сигнала x[n], ![]() - амплитудный спектр (функция
модуля X(e jω)),
- амплитудный спектр (функция
модуля X(e jω)), 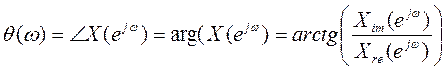 - фазовый спектр (функция фазы
X(e jω)) сигнала
x[n].
- фазовый спектр (функция фазы
X(e jω)) сигнала
x[n].
Особенность (свойство) ДВПФ: сигнал
x[n] – дискретный
по аргументу, спектр Фурье ![]() -
непрерывный по аргументу ω.
-
непрерывный по аргументу ω.
Характерное отличие ДВПФ от непрерывного преобразования ПФ состоит также в том, что оно является периодическим по аргументу ω с периодом 2π, в то время как НВПФ X(jω)- апериодическая функция ω. Действительно,
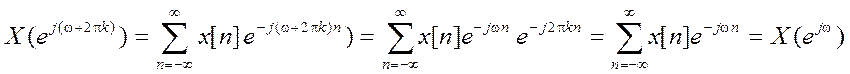 .
.
Ввиду периодичности 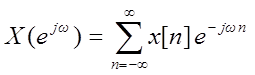 представляет
собой ряд Фурье по переменной ω. Выражение для коэффициентов этого ряда
представляет
собой ряд Фурье по переменной ω. Выражение для коэффициентов этого ряда
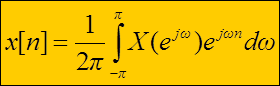 .
.
и есть обратное ДВПФ (ОДВПФ, англ. IDTFT), которое называют также выражением синтеза сигнала x[n] по его спектру.
Доказательство:
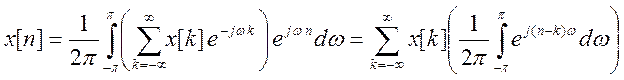 .
.
Интеграл
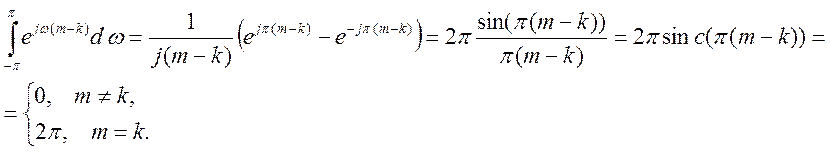
Поэтому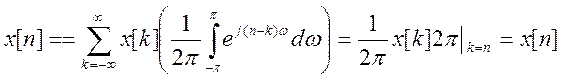
Получено тождество, следовательно, формула обратного ДВПФ – верна.
В случае дискретизации сигнала x(t) с интервалом отсчетов ![]()
выражения ДВПФ приобретают вид:
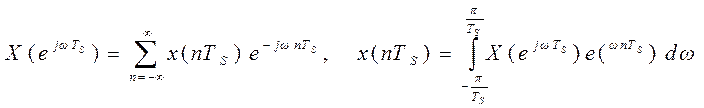
Во второй части курса после знакомства с Z – преобразованием будет строго показано, что ДВПФ может рассматриваться как Z – преобразование дискретного сигнала на мнимой оси комплексной плоскости z
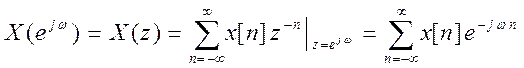 .
.
Пример 1. Определим ДВПФ сигнала ![]()
Представим этот сигнал в виде суммы (комбинации) двух сигналов
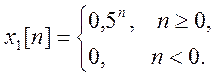 и
и 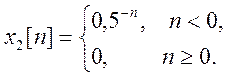 ДВПФ этих сигналов
ДВПФ этих сигналов
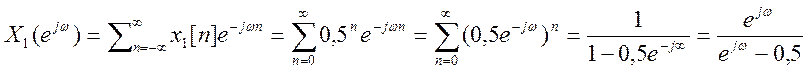 ,
,
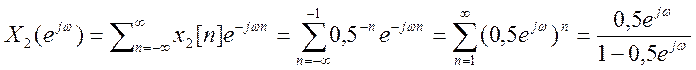
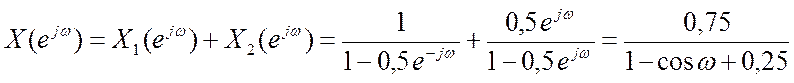
Графики сигнала и его амплитудного и фазового спектра
|
|
|
|
Пример 2. Найдем ДВПФ дискретного прямоугольного импульса
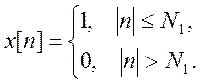
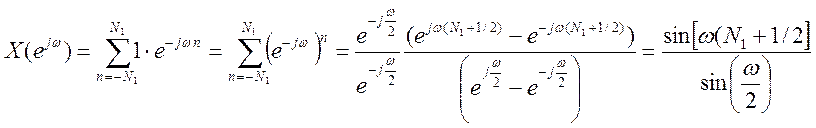 .
.
В преобразовании этого выражения использована формула суммы
конечной геометрической прогрессии. Если ![]() ,
то
,
то
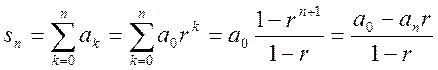
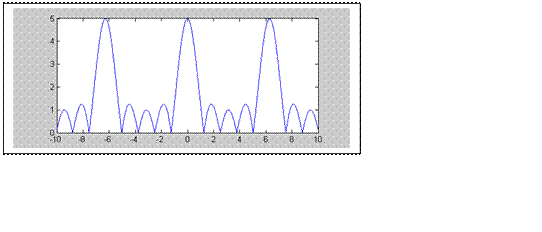
Действительно, здесь ![]() .
.
Ниже приведен график амплитудного спектра ![]() для N1
= 2.
для N1
= 2.
|
Найдем ДВПФ комплексной гармоники, определяемой выражением
![]() .
.
ДВПФ этого сигнала
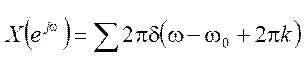 ,
где
,
где ![]() - дельта функция от ω, k=1,2,3,…
- дельта функция от ω, k=1,2,3,…
Для доказательства возьмем ОДВПФ от X(ejω)
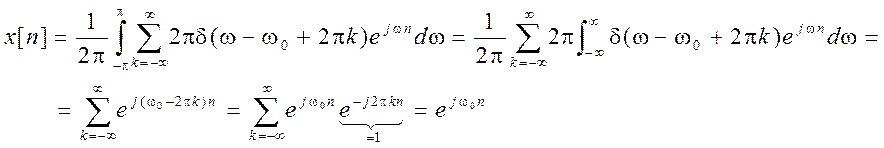
Сравните этот результат с 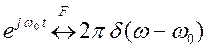 для
сигналов непрерывного времени.
для
сигналов непрерывного времени.
Условие сходимости ДВПФ
Бесконечный ряд 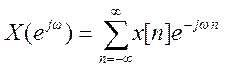 может
сходиться или расходиться. Условие сходимости ДВПФ
может
сходиться или расходиться. Условие сходимости ДВПФ
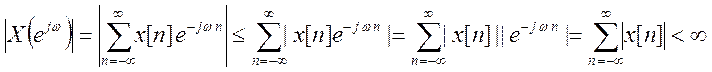 , т.е. требуется абсолютная
сходимость x[n], или
, т.е. требуется абсолютная
сходимость x[n], или
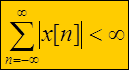 . Поскольку
. Поскольку 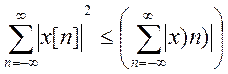 , то абсолютная сходимость выполняется
для сигналов с конечной энергией.
, то абсолютная сходимость выполняется
для сигналов с конечной энергией.
Обратное ДВПФ
Выражение 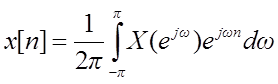 используется для определения
сигнала x[n] по
его спектру Фурье.
используется для определения
сигнала x[n] по
его спектру Фурье.
Пример. Пусть ![]() ,
определим x[n].
,
определим x[n].
Запишем
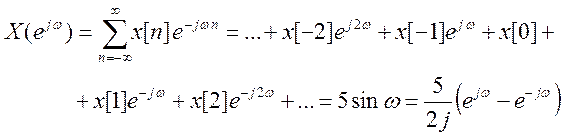
Непосредственное сравнение левой и правой части дает
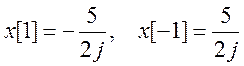 .
.
Отсюда
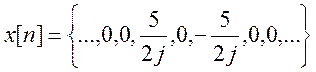 .
.
Использованный в примере метод называется методом разложения в степенной ряд.
Кроме этого метода используется также метод разложения на простые дроби, который будет подробно рассматриваться во второй части курса.
Вычисление ДВПФ в MatLAB
Для вычисления ДВПФ может использоваться приведенная ниже файл – функция, основанная на использовании встроенной в Matlab функции fft().
function [X,w] = DTFT(x,M)
% Функция вычисляет значения DTFT от вектора x.
% Обращение
% [X,w] = DTFT(x,0)
% здесь X - вектор значений DTFT,
% w - вектор угловых частот.
% Если желательно вычислить DTFT с M значениями частоты,
% используется обращение
% [X,w] = DTFT(x,M)
% Этот вариант используется, когда размер вектора x
% меньше размера вектора частот w,
% при этом x дополняется нулевыми значениями
N = max(M,length(x));
% Приведение FFT к размеру 2^m
N = 2^(ceil(log(N)/log(2)))
% Вычисление fft
X = fft(x,N);
% Вектор частот
w = 2*pi*( (0:(N-1))/N );
w = w - 2*pi*(w>=pi)
% Сдвиг FFT к интервалу от -pi до +pi
X = fftshift(X);
w = fftshift(w);
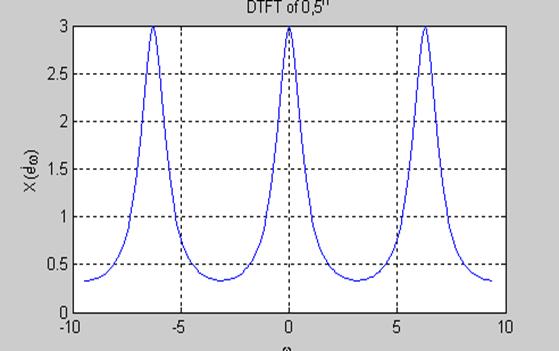
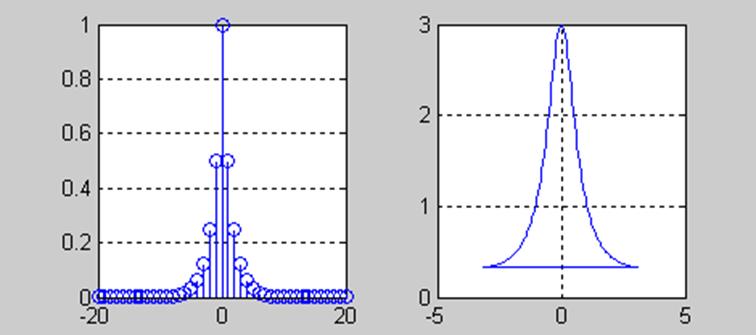
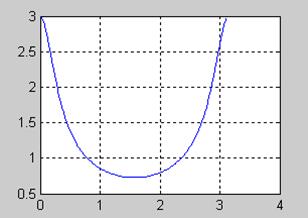
Пример. Пусть ![]() Определим
ДВПФ этого сигнала и построим график амплитудного спектра.
Определим
ДВПФ этого сигнала и построим график амплитудного спектра.
Код Matlab
n=-20:20;
x=0.5.^abs(n);
[X,w]=DTFT(x,128);
subplot(121)
stem(n,x), grid
subplot(122),
plot(w, abs(X))
grid
Для вычисления ДВПФ может также использоваться функция freqz() Matlab. При этом функция X(ejω) должна быть рациональной функцией вида
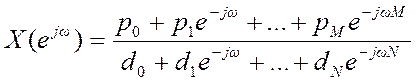 .
.
Функция freqz()
имеет несколько форм синтаксиса. В самой простой из них
[h, w] = freqz(num, den, n) она возвращает n комплексных значений X(ejω) в диапазоне
ω от 0 до π по значениям коэффициентов полинома числителя num и полинома знаменателя den. По умолчанию n = 512.
Пример. Пусть 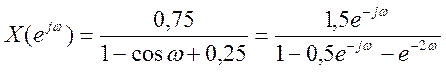 .
.
Код Matlab
 num=[0
1.5];
num=[0
1.5];
den=[1 -0.5 -1];
[X w1]=freqz(num, den, 128);
plot(w1, abs(X)), grid
Свойства ДВПФ
ДВПФ имеет свойства, аналогичные свойствам НВПФ.
В таблице перечислены наиболее важные из этих свойств.
|
Свойство |
Временная область (Time domain) |
Частотная область (Frequence domain) |
3. Частотный сдвиг
5.
Реверсирование во времени
|
x[n-k]
|
функция ω
|
|
8. Дифференцирование
9. Теорема |
|
|
Рассмотрим доказательства наиболее важных из этих свойств
1. Докажем свойство временного сдвиг ![]()
Пусть ![]() , тогда
, тогда 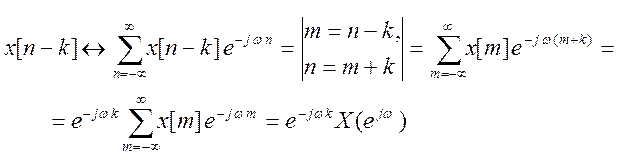
В частности, для 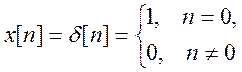
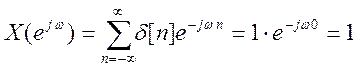 , отсюда
, отсюда ![]() ,
,
т.е., сдвиг x[n] на k тактов
во времени вызывает фазовый сдвиг ![]() на
на ![]()
2. Теорема
Парсеваля. Энергия сигнала 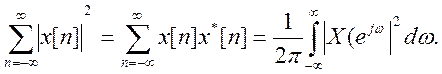
Согласно обратному ДВПФ 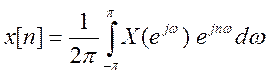 . Отсюда
. Отсюда
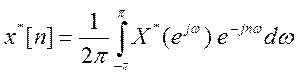 ,
следовательно,
,
следовательно,
Энергия =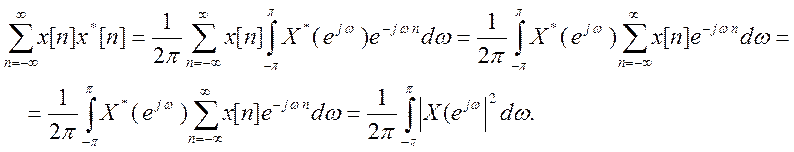
Равенство Парсеваля позволяет определить энергию сигнала в частотной области, если это упрощает вычисление. Иногда это так.
Свойство свертки ДВПФ
Свертке двух последовательностей во временной области отвечает произведение их дискретных преобразований Фурье в частотной области
![]() . Доказательство.
Положим
. Доказательство.
Положим 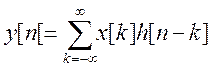 ,
,
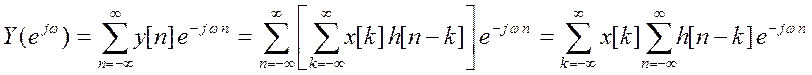 .
.
Заменим ![]() , при этом
, при этом
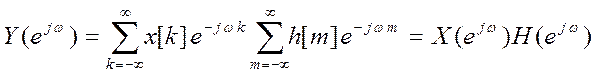 .
.
Таким образом, свертке во временной области соответствует
произведение спектров в частотной области 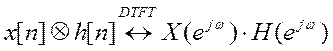
Рассмотрим пример применения свойства свертки.
Пример.
Пусть 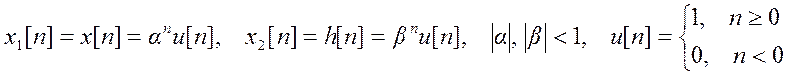
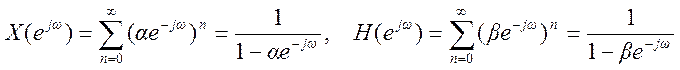 .
.
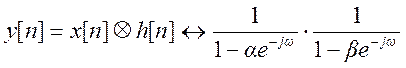 - рациональная функция
(отношение полиномов) от
- рациональная функция
(отношение полиномов) от ![]() .
.
Разложим y[n] на простые дроби.
Если 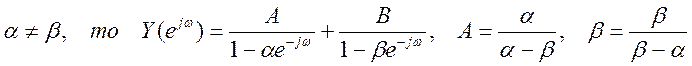 . Следовательно,
. Следовательно,
![]() .
.
Связь импульсной и частотной характеристик линейной дискретной системы
Во временной области линейные дискретные во времени системы (ЛДС) описываются линейными разностными уравнениями вида
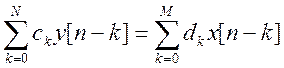 ,
,
где ![]() - входной сигнал,
- входной сигнал,
![]() - выходной
сигнал,
- выходной
сигнал,
![]() - коэффициенты
уравнения.
- коэффициенты
уравнения.
Возьмем ДВПФ от обеих частей уравнения, при этом по свойству временного сдвига
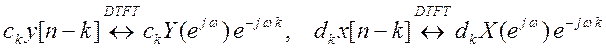 .
.
С учетов свойства линейности получим в частотной области
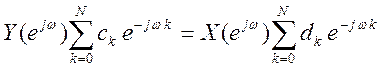 .
.
Отношение
ДВПФ выхода и входа 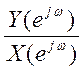 есть частотная
характеристика ЛДС
есть частотная
характеристика ЛДС 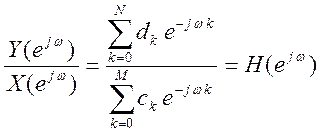 .
.
При этом 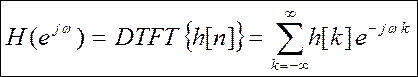
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.