Министерство общего и профессионального образования Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра автоматики
Дисциплина «Теория и обработка сигналов», 5 - й семестр
Расчетно-графическая работа
Выполнила: Проверил:
Группа: АИ-42 Еленычев С.В.
Студентка: Ахтямова Г.С.
Последняя цифра шифра в зачетной книжке: 1
НОВОСИБИРСК
2006
1.Раздел 1
1.1. Записанные в показательной (полярной) форме
комплексные числа (выражения)
а)
![]() ,
,
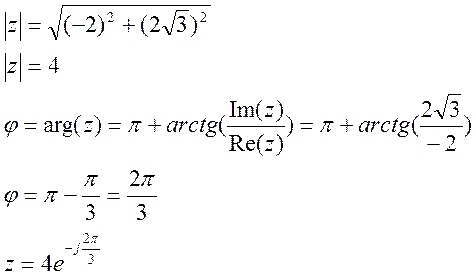
б)
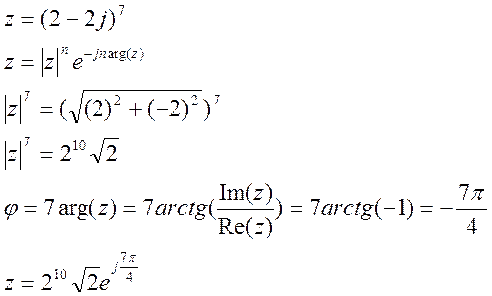 ,
,
в)
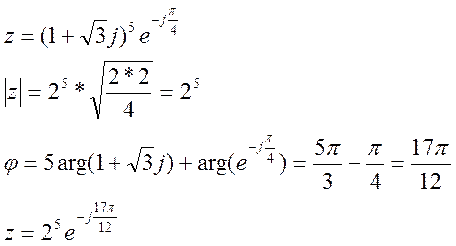
Ответ:
а) ![]()
б) ![]()
в) 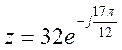
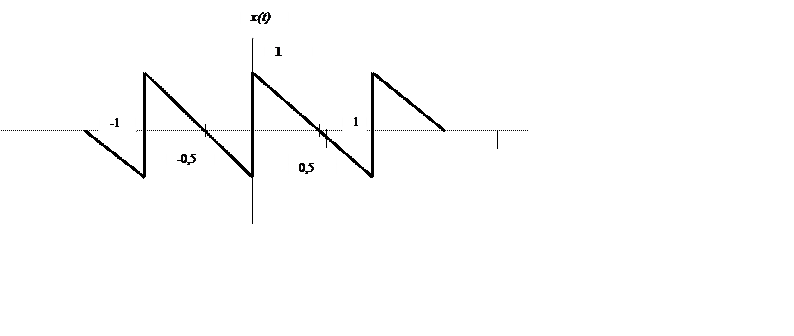
1.2 Сигнал x(t) имеет вид

Найдено x(3t-2).
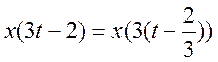
То есть сначала нам нужно сдвинуть исходный график на 2/3,а потом сжать по оси абсцисс в 3ри раза.
Ответ:
2.Раздел 2
2.1. Определение коэффициентов Фурье сигнала и построение его амплитудного и фазового спектра
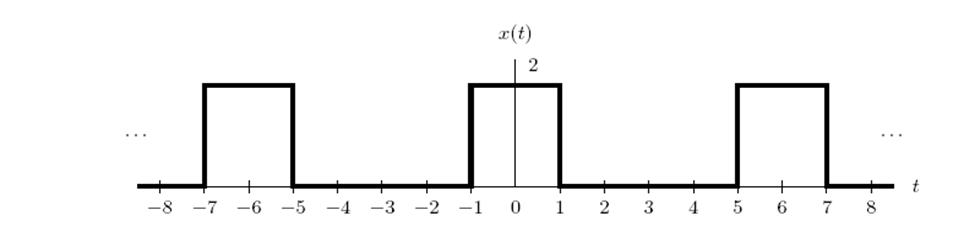
Для![]()
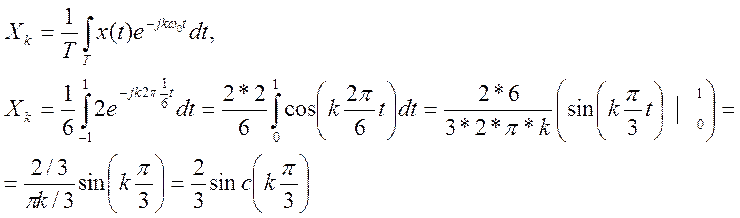
Если к=0, то 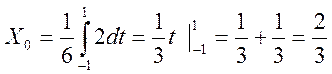
Графики амплитудного и фазового спектра сигнала.
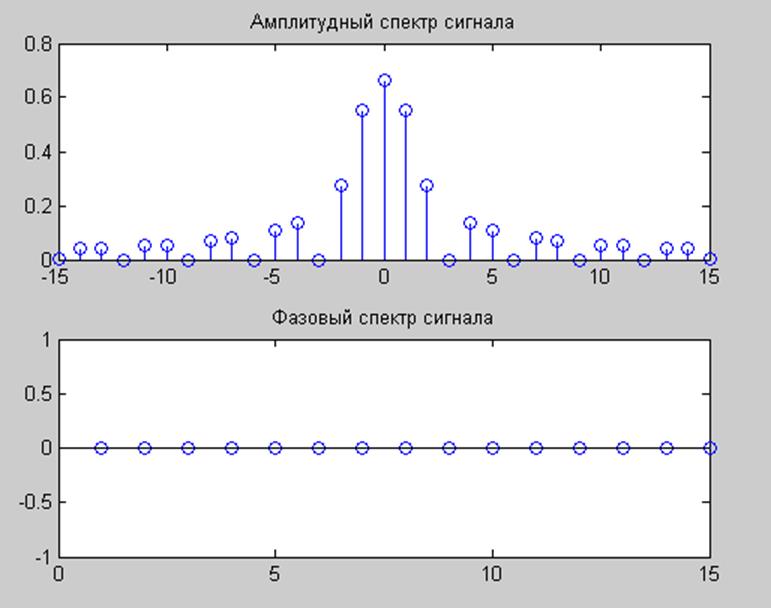
Ответ: 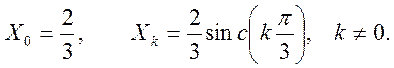
2.2. Нахождение коэффициентов Фурье сигнала
 |
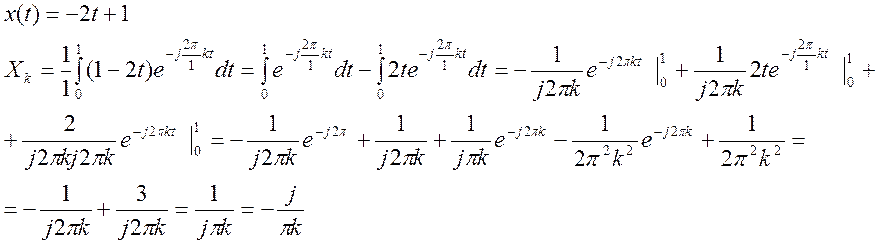
Если к=0, то 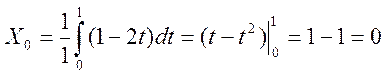
Ответ:
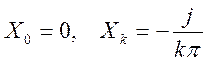
3.Раздел 3
3.1.Определение преобразования Фурье и построение графика амплитудного спектра сигнала
![]() .
.
Представим
сигнал x(t) в виде суммы двух сигналов ![]() и
и
![]()
График амплитудного спектра сигнала имеет вид (а=1,К=2):
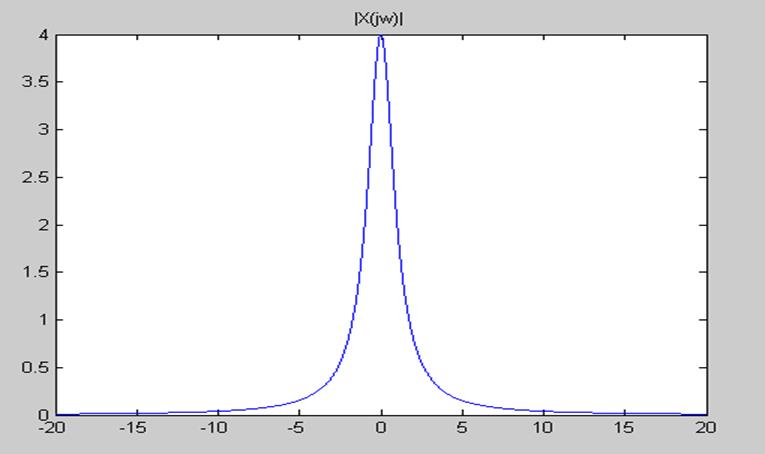
Ответ: 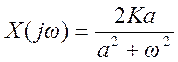
3.2. Вычисление
преобразования Фурье сигнала типа синусоидального импульса
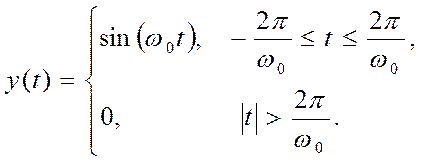
Решение.
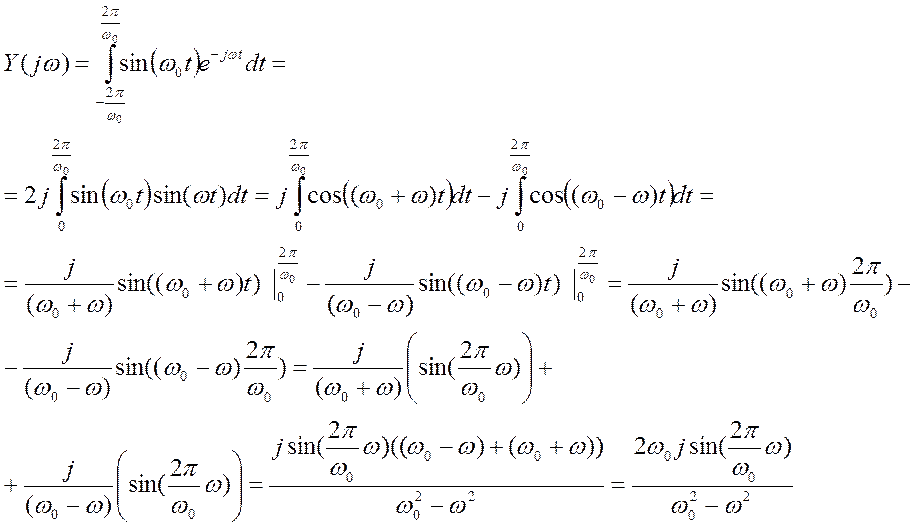
Ответ: 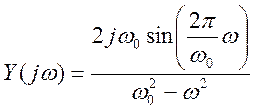
4. Раздел 4.
4.1. Определение ДВПФ сигнала и изображение графика его амплитудного спектра
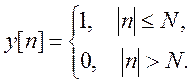
Решение.
По формуле суммы конечной геометрической прогрессии
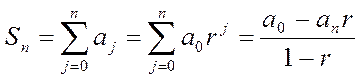 .
.
Поэтому
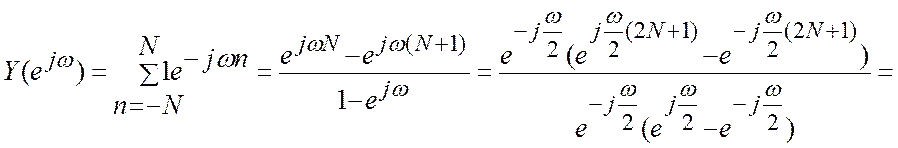
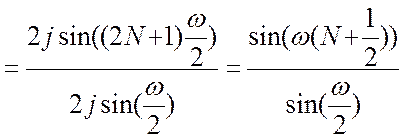
В преобразовании
используется выделение множителя 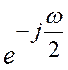 и формула
и формула
Эйлера.
График амплитудного спектра для N = 4
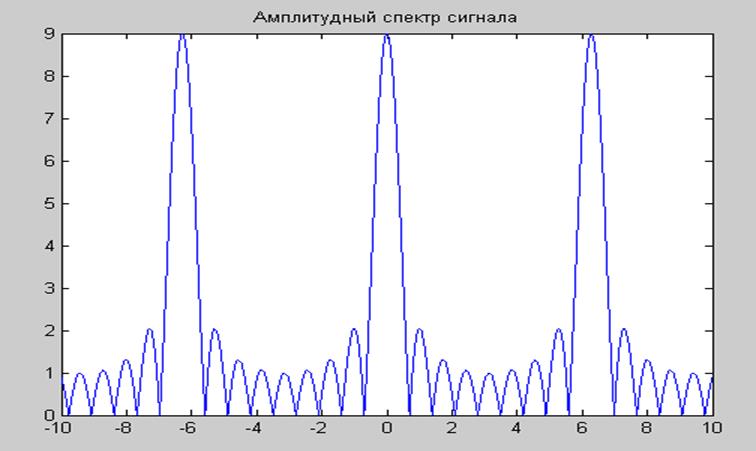
Ответ: 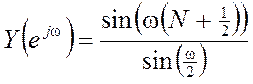 .
.
4.2. Нахождение ДВПФ сигнала
![]()
Решение.
Представим этот сигнал в виде суммы (комбинации) двух сигналов
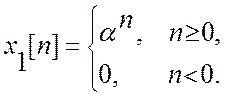 и
и 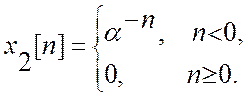
ДВПФ этих сигналов
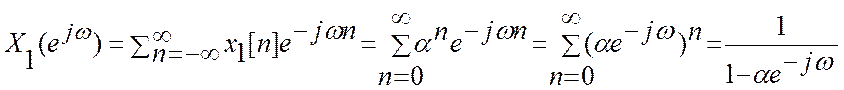
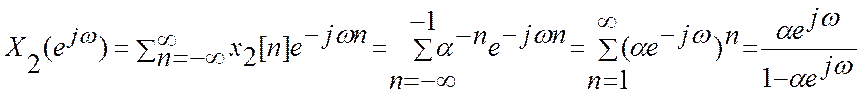
В
преобразовании этих выражений использована формула суммы бесконечно убывающей геометрической
прогрессии.Если ![]() , то
, то
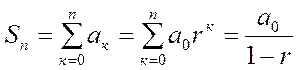
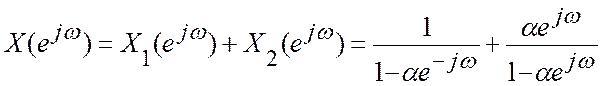
5. Раздел 5.
5.1.
Определите значения свертки двух
дискретных сигналов:
![]() и
и ![]() .
Изобразите графики x[n], h[n] и
.
Изобразите графики x[n], h[n] и ![]() .
.
![]()
Решение.
![]()
Графики x[n] и h[n]
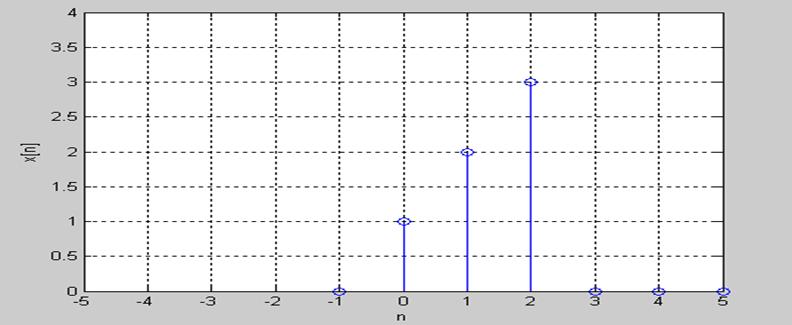
Рис.1. График x[n]
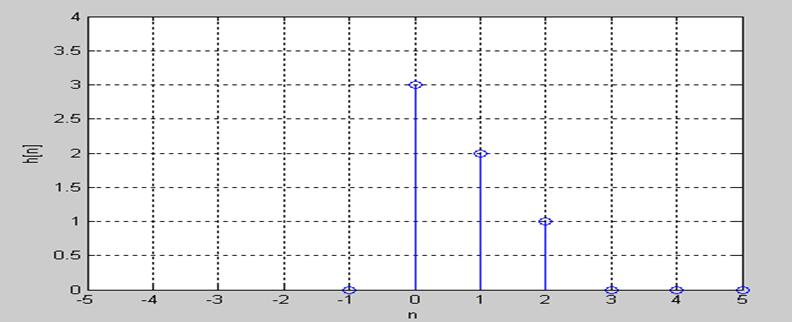
Рис.1. График h[n]
Реверсируем h[k] относительно начала координат
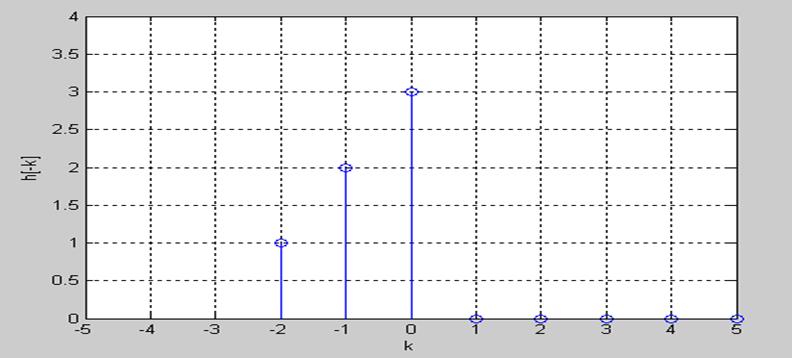
Разбиваем ось n на 5 значений.
1)
Для ![]() ,
x[k] и h[n-k]
перекрываются при
,
x[k] и h[n-k]
перекрываются при ![]()
![]()
2)
Для ![]()
![]() при
при ![]() и
и
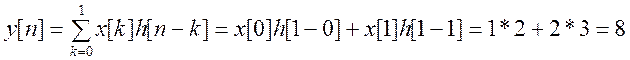
3)
Для ![]()
![]() при
при ![]() и
и
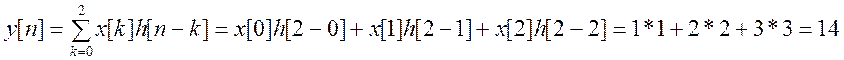
4)
Для ![]()
![]() при
при ![]() и
и
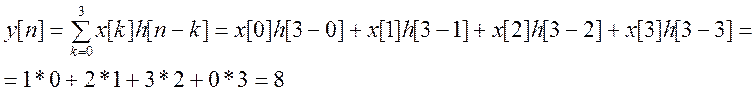
5)
Для ![]()
![]() при
при ![]() и
и
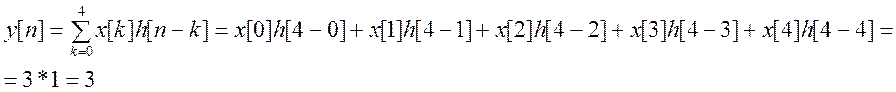
Окончательный результат по вычислению свертки
![]()
График
![]()
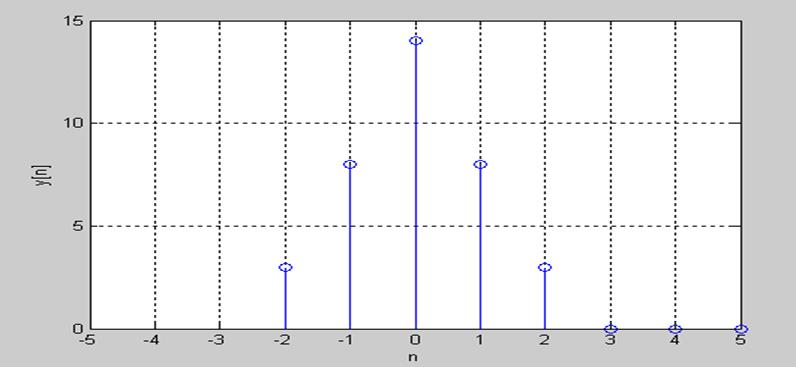
Рис.3.График
![]()
5.2.Вычисление
свертки двух непрерывных сигналов и изображение её графика
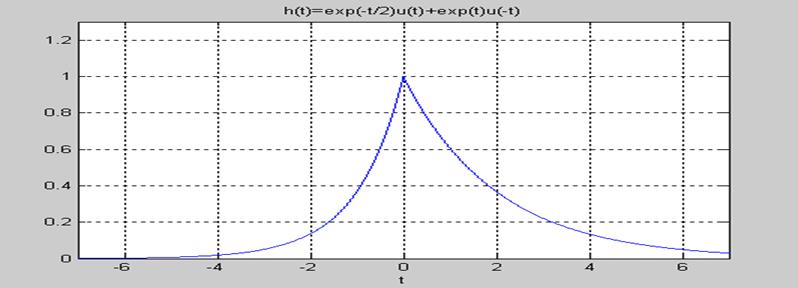
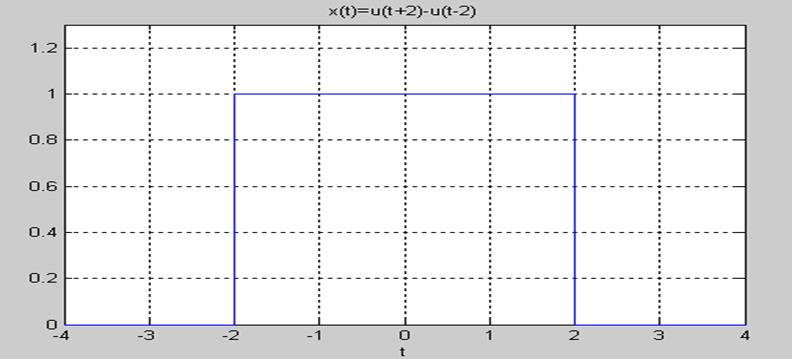
Решение.
Интеграл
непрерывной свертки имеет вид ![]() .
.
В соответствии с геометрическим смыслом операция свертки заключается в зеркальном отражении одной из участвующих в свертке функций, сдвиге её на значение t, перемножении операндов и интегрировании результата перемножения.
Зеркально отражать
будем x(![]() )
)
Интервал интегрирования при этом разбивается на следующие подинтервалы
1)
![]()
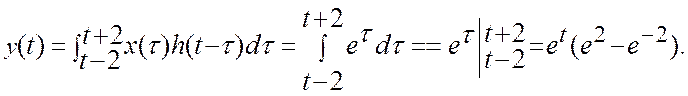
2)
![]()
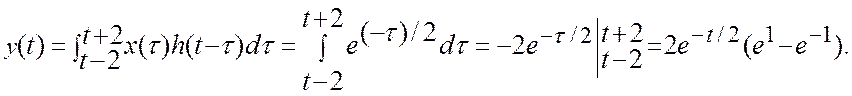
3)
![]()
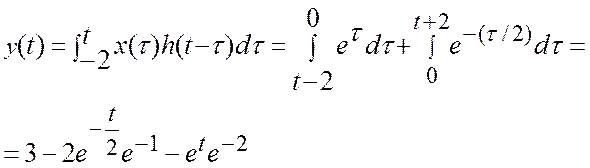
Таким образом, результат свертки
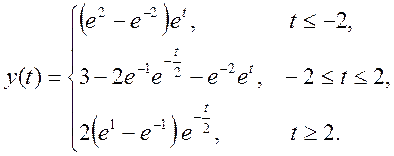
График свертки
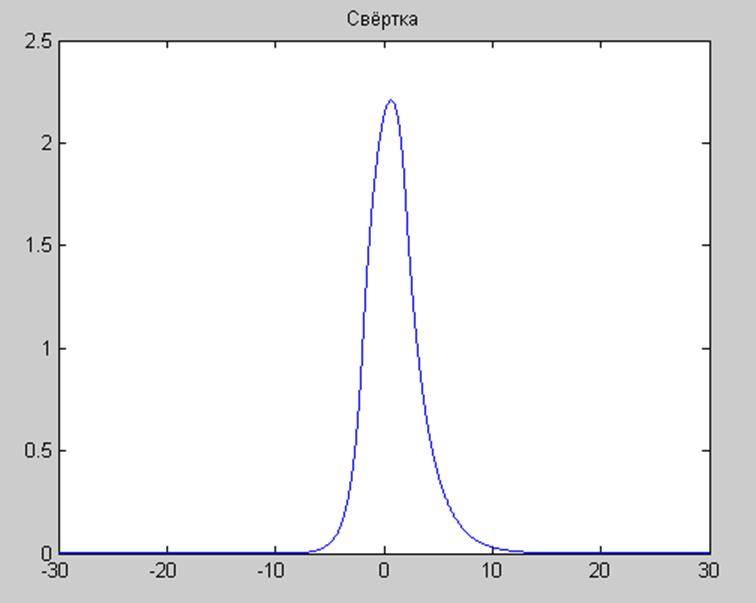
Ответ:
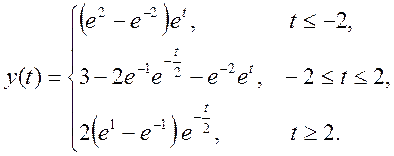
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.