Билет №1. Операции на множествах и их свойства (с доказательством).
Множеством будем называть некоторую совокупность элементов произвольного рода.
Объединением множеств А и В называется множество, каждый элемент которого принадлежит хотя бы одному из этих двух множеств.
А![]() В={x│x
В={x│x![]() A или x
A или x![]() B}.
B}.
Пересечением множеств А и В называется множество, элементы которого являются одновременно элементами обоих множеств.
А![]() В={x│x
В={x│x![]() A и x
A и x![]() В}.
В}.
Разностью множеств А и В называется множество, каждый элемент которого принадлежит множеству А, но не принадлежит множеству В.
A\B={x│x![]() A и x
A и x![]() B}.
B}.
Дополнением множества А называется разность между универсальным множеством и множеством А.
Ā=U\A.
Универсальное множество U – множество, для которого в ходе какого-либо рассуждения все множества являются подмножествами.
Множество В является подмножеством множества А, если всякий элемент В является элементом А.
Симметрическая разность. ![]()
![]()
Свойства операций над множествами.
Пусть задан универсум U. Тогда ![]() A, B, C
A, B, C ![]() U выполняются следующие свойства
U выполняются следующие свойства
А![]() А=А,
А
А=А,
А![]() А=А
А=А
А![]() В=В
В=В![]() А, А
А, А![]() В=В
В=В![]() А
А
3. ассоциативность:
А![]() (В
(В![]() С)=(А
С)=(А![]() В)
В)
![]() С, А
С, А![]() (В
(В![]() С)=(А
С)=(А![]() В)
В)
![]() С
С
А![]() (В
(В![]() С)=(А
С)=(А![]() В)
В)
![]() (А
(А![]() С),
А
С),
А![]() (В
(В![]() С)=(А
С)=(А![]() В)
В) ![]() (А
(А![]() С)
С)
![]() =А
=А
![]() =
=![]()
![]()
![]() ,
, ![]() =
=![]()
![]()
![]()
(А![]() В)
В)![]() ( А
( А![]() )=А,
(А
)=А,
(А![]() В)
В)![]() ( А
( А![]() )=А
)=А
А![]() (А
(А![]() В) =А, А
В) =А, А![]() (А
(А![]() В) =А
В) =А
Константа – универсальное, пустое множество.
![]()
![]()
А![]() =
=![]() ; А
; А![]() =U
=U
![]() ;
; ![]()
Билет №2. Теорема о мощности декартова произведения конечных множеств.
Множества могут быть конечными и бесконечными. Мощность конечного множества равна числу элементов в нем. Обозначение мощности │А│. Если множество А не содержит ни одного элемента, то оно называется пустым: │А│=0.
Декартовым произведением множеств
А и В (А×В) называется множество всех пар (a,b), таких что a![]() А, b
А, b![]() В.
В.
А,В – множества произвольной природы
![]()
Свойства:
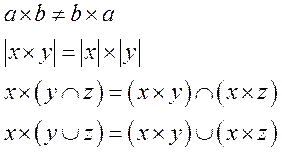
Теорема. Пусть даны А1, А2,
…, Аn – конечные множества и │А1│=
m1, │A2│=
m2, …, │An│=
mn. Тогда мощность множества А1 ![]() А2
А2 ![]() …
… ![]() Аn равна произведению мощностей
А1, А2, …, Аn:
Аn равна произведению мощностей
А1, А2, …, Аn:
│А1 ![]() А2
А2 ![]() …
… ![]() Аn│= m1m2… mn
Аn│= m1m2… mn
Доказательство (с помощью математической индукции):
Вектор – упорядоченный набор элементов. Длина вектора – число координат.
Пример:
Сколько существует пятизначных натуральных чисел?
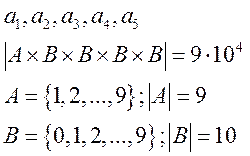
Билет №3. Теорема о мощности булеана конечного множества.
Множество всех подмножеств множества A называется булеаном и обозначается В(А). Множество В является подмножеством множества А, если всякий элемент В является элементом А.
Пример:
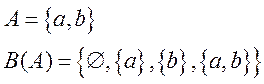
Теорема. Для конечного множества А{а1,а2,…аn} │В(А) │=2n
Доказательство:
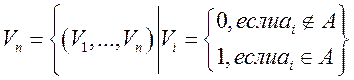
(Vn-множество двоичных векторов из нулей и единиц длины n)
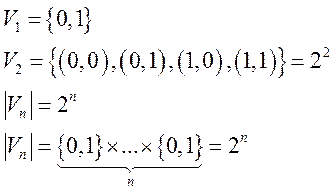
Установим взаимнооднозначное соответствие(т.е. биекцию) между булеаном и Vn.
![]()
Пусть ![]()
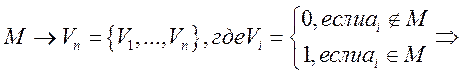 это
биекция
это
биекция
Пример:
Если ![]() ,
то подмножеству
,
то подмножеству ![]() соответствует вектор
соответствует вектор ![]()
Билет №4. Теорема о счетности множества рациональных чисел.
Счетным множеством называется множество, равномощное множеству натуральных чисел (множества А и В равномощны, если существует взаимнооднозначное соответствие)
Теорема. Множество рациональных чисел счетно.
Доказательство:
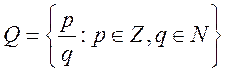 , где Q
– множество рациональных чисел.
, где Q
– множество рациональных чисел.
Пусть ![]() - рациональное
число, где p,q- целые.
- рациональное
число, где p,q- целые.
![]() - высота дроби.
- высота дроби.
h=1 1дробь ![]()
h=2 множество дробей 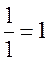 ,
, 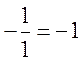
и т.д. нумеруя дроби в порядке увеличения высот мы получим биекцию между N и Q, т.е. Q счетно.
Билет №5. Теорема о несчетности множества действительных чисел.
Теорема. Множество действительных чисел несчетно.
Доказательство:
Рассмотрим интервал действительных
чисел [0,1] ![]() R. Предположим,
что оно счетно и существует его нумерация. Расположим все числа, изображенные
бесконечными десятичными дробями, в порядке этой нумерации:
R. Предположим,
что оно счетно и существует его нумерация. Расположим все числа, изображенные
бесконечными десятичными дробями, в порядке этой нумерации:
0,a11a12a13…
0,a21a22a23…
0,a31a32a33…
……………..
Рассмотрим любую бесконечную десятичную дробь 0,b1b2b3…, такую что b1≠a11; b2≠a22; b3≠a33 и т.д. Эта дробь не может войти в указанную последовательность, так как от первого числа она отличается первой цифрой, от второго числа – второй цифрой и т.д. Следовательно, все числа не могут быть пронумерованы, и множество всех действительных чисел несчетно. Его мощность называется континуум.
Билет №6. Теорема о разбиении основного множества на классы эквивалентности.
Отношением эквивалентности называется бинарное отношение на множестве, если оно рефлексивно, симметрично и транзитивно.
1. a~a рефлексивность
2. a~b=b~a симметричность
3. a~b и b~c ![]() a~c транзитивность
a~c транзитивность
Разбиением множества А называется совокупность попарно не пересекающихся подмножеств А таких, что каждый элемент множества А принадлежит только одному из этих подмножеств.
Пример:
![]()
тогда ![]() - разбиение
множества Х.
- разбиение
множества Х.
Классом эквивалентности называется подмножество, состоящее из элемента а и всех элементов эквивалентных а.
Теорема. Эквивалентность(реф., сим., транз.) разбивает основное множество на классы эквивалентности, т.е.
Доказательство:
![]() a
a![]() c, b
c, b![]() c
c
c![]() a, c
a, c![]() b(cим.) (по транз.)
b(cим.) (по транз.) ![]() a
a![]() b
b ![]() b
b![]() Ca
(получилось противоречие)
Ca
(получилось противоречие)
Выясним, что класс эквивалентности не зависит от представителя, который мы выбираем из этого класса.
a![]() Ca и b
Ca и b![]() Ca
Ca
![]()
a![]() b или b
b или b![]() c (по транзитивности)
c (по транзитивности) ![]()
![]()
Билет №7. Частично упорядоченные множества, диаграмма Хассе.
Рефлексивное, антисимметричное и транзитивное отношение называется отношением частичного порядка на множестве.
Отношение частичного порядка на множестве Х, для которого любые два элемента сравнимы, называется отношением линейного порядка.
![]()
Множество Х, на котором задано отношение частичного порядка, называется частично упорядоченным (≤реф.+антисим.+транз.).
Говорят, что y покрывает x, если x<y и не существует такого элемента u, что x<u<y
Всякое частично упорядоченное множество можно изобразить на диаграмме Хассе. Изображая точками элементы отношения, а имеющиеся связи между элементами изображать отрезками.
Пример:
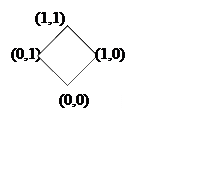
![]()
диаграмма Хассе для ЧУМа.
Элемент а![]() А
называется max, если из того что а≤х
А
называется max, если из того что а≤х ![]() х=а.
х=а.
Элемент а![]() А
называется min, если из того что x≤a
А
называется min, если из того что x≤a ![]() х=а.
х=а.
Элемент а![]() А
называется наибольшим, если а≥х для любого х
А
называется наибольшим, если а≥х для любого х![]() А.
А.
Элемент а![]() А
называется наименьшим, если а≤х для любого х
А
называется наименьшим, если а≤х для любого х![]() А.
А.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.