Операции на множествах и их свойства. Теорема о мощности декартова произведения конечных множеств. Теорема о счетности множества рациональных чисел. Изоморфизмы и автоморфизмы алгебр, страница 4

Изоморфные графа отличаются лишь обозначением вершин.

Отображение φ называется изоморфизмом между G и H, если же графы совпадают, то автоморфизмом (изоморфизм на себя).

Группа автоморфизмов – все изоморфизмы графа на себя.

Для автоморфизмов справедливы следующие утверждения:

1. Множество всех автоморфизмов данного графа относительно их композиций, т.е. последующего выполнения, образуют группу, которую обычно обозначают Aut G1
2. Группа автоморфизмов графов вкладывается в группу всех подстановок длины равной мощности.
3. Aut k_nS_n
4.  При изоморфизме степени вершины и ее образа совпадают, Δ переходит в Δ и т.д.

Билет №21. Критерий эйлеровости и полуэйлеровости графа. Гамильтоновы графы.

Эйлеровы графы.

Задача о Кенигсбергских мостах.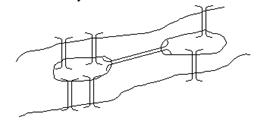

       Можно ли пройти через каждый мост один раз и попасть в ту же точку.

    Существует ли циклический маршрут, содержащий каждое ребро в точности один раз.

          Граф называется эйлеровым грфом, если  в нем существует циклический маршрут, содержащий каждое ребро в точности один раз.

Граф называется полуэйлеровым, если для него существует маршрут (не циклический), содержащий каждое ребро в точности один раз.

В обоих случаях вершины можно проходить неоднократно. Очевидно, что любой эйлеров граф, является полуэелеровым.

Теорема (критерий эйлеровости).

Граф является эйлеровым тогда и только тогда, когда он связен и все степени его вершин четны.

Доказательство:

Необходимость:

Доказать, что степени вершин эйлерова графа G четны. Т. к. граф эйлеров, то существует эйлеров цикл, который проходит через все ребра исходного графа. Возьмем произвольную вершину v V, G = (V, E). Т. к. граф G Эйлеров, то вершина v Эйлерову циклу. Пусть эта вершина встречается ровно k раз в Эйлеровом цикле, т.е. ровно k раз вошли и вышли из нее по новым не пройденным ребрам.

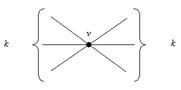
Т.к. эйлеров цикл содержит все ребра исходного графа. Тогда степень вершины v равна 2k, т.е. четна. А так как v произвольная вершина исходного графа, то все вершины имеют четную степень.

Достаточность:

Пусть G-связен и степени всех его вершин четны. Т.к. в графе нет изолированных вершин, то степени всех его вершин четные и не меньше 2.

по лемме (если в графе степени всех вершин не меньше 2, то он содержит цикл) в G  цикл С. Выбросив из графа G все ребра, лежащие в цикле С, получим граф Н.

, на n вершинах, что и граф G (число ребер в Н  число ребер в G). В этом графе степени всех вершин тоже четны.

По индукционному предположению в каждом компоненте H_i  эйлеров цикл С_i.

Строим эйлеров маршрут в G следующим образом:

начинаем с произвольной точки цикла С, проходим точки которые изолированы в графе H без остановки. Дойдя до первой не изолированной вершины в графе Н проходим по эйлерову циклу компонентой H_i, которая касается этого цикла и т.д.

Теорема.

Граф является полуэйлеровым тогда и только тогда, когда в нем не более двух вершин(одной вершины не может быть из леммы о рукопожатиях).

          Граф называется гамильтоновым графом, если  он содержит цикл, проходящий через каждую вершину ровно один раз.

 

Если цикл заменить на произвольный путь, то это будет полугамильтоновый граф.

Билет №22. Нижняя и верхняя оценки числа ребер простого графа.

Граф называется простым, если каждую пару вершин соединяет не более чем одно ребро.

Нижняя.

Лемма: В полном графе на n вершинах число ребер удовлетворяет неравенствам:

n - 1 ≤ m ≤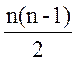

Теорема:

В простом графе G на n вершинах с k компонентами связности чисто ребер m удовлетворяет неравенствам

n - k ≤ m ≤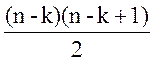

Доказательство: Индукция по числу ребер m.

1.  База: m = 0 =>G – пустой граф => k=n; n - k = 0 ≤ m

2. Шаг индукции:

Пусть m₀ – минимальное число ребер в графе на n вершинах, с k компонентами, т.е. если мы из этого графа выбросим какое-нибудь ребро, то число компонентов станет k+1. мы получим новый граф на n вершинах с k+1 компонентами и m₀-1 ребром  => =>     n – k ≤m₀

Верхняя.

Пусть  каждая компонента связанности является полным графом.

 

Возьмем две из них C_i и C_j, причем n_i, n_j – числа их вершин и  1<.

  Уберем в графе C_i  одну вершину, а в графе C_j, одну вершину добавим, и дополним до полного связями с остальными.

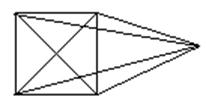тогда число вершин и компонент связанности в новом графе тоже самое, а число ребер по крайней мере не уменьшится. Проделывая эту процедуру несколько раз мы получим полный на n-(k-1) вершинах. Число ребер в полном графе по лемме равно .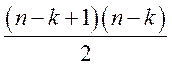

Следствие:

Если в любой  простом графе на n вершинах число ребер больше чем 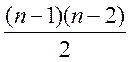 , то он связен.

Доказательство:

Представим k=2 верхней оценкой. Получим: 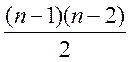, но при k=2 не связен, 2 компоненты быть не могут и тем более больше.

Билет № 23. Двудольные графы. Задача о свадьбах. Теорема Холла.

Граф G=(V,E) называется двудольным графом, если множество его вершин можно разбить на два непересекающихся множества V₁ и V₂ (V₁ ∩ V₂=Ø, а V₁ U V₂ = V) таким образом, что в V₁ никакие две вершины не связаны между собой, аналогично в V₂.

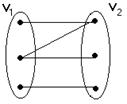
Граф называется полным двудольным графом, если каждая вершина из V₁ соединена с каждой вершиной V₂.

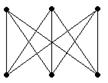
Задача о свадьбах.

Имеется m юношей знакомых с определённым числом девушек. Можно ли поженить юношей так, чтобы каждый юноша был женат на знакомой девушке.

v₁ = {b₁ … b₄}    v₂ = {g₁ … g₅} 

b₁ – g₁ g₂

b₂ – g₃

b₃ – g₄ g₅ g₁

b₄ – g₂ g₄

На языке теории графов: можно ли осуществить биекцию между множеством вершин V₁ и V₂ таким образом, чтобы каждой вершине из V₁ соответствовало какое то множество вершин из V₂.

            Терема Холла (1935)

Задача о свадьбах имеет решение, когда любые k юношей 1 ≤ k < m (m - все юноши) знакомы по крайней мере с k девушками.

            Доказатьльство:

Необходимость: