Правило сложения:
Пусть A - множество из m
элементов; B - множество из n элементов;
если A ∩ B= Ø, то ![]()
![]()
Билет №13.Сочетания без повторений и их число. Связь с биномом Ньютона.
r-сочетанием из
множества А=![]() называется любое подмножество
мощности r (или если элементы неупорядоченной r-выборки попарно различны). r-сочетания
различаются только составом, порядок в них не важен.
называется любое подмножество
мощности r (или если элементы неупорядоченной r-выборки попарно различны). r-сочетания
различаются только составом, порядок в них не важен.
Если порядок следования элементов в выборке не является существенным, то такая выборка называется неупорядоченной.
Пример:
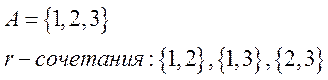
Теорема. Число всех
r-сочетаний из множества А, равно 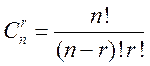 .
.
Доказательство:
Доказано, что общее количество всех упорядоченных r-элементных подмножеств равно 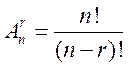 .
.
Мы знаем, что число способов
упорядочить r элементное подмножество равно ![]() . Следовательно, число выборок будет в
r! раз больше числа сочетаний. Следовательно,
. Следовательно, число выборок будет в
r! раз больше числа сочетаний. Следовательно, 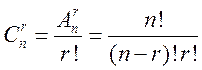 .
.
Пример:
Сколько баскетбольных команд можно составить из 10 человек?
Ответ: 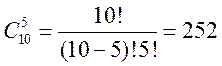
Бином Ньютона.
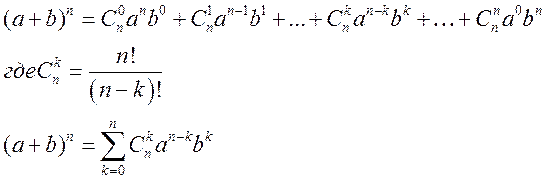
(подмножество в множестве 0)
Эта сумма равна числу подмножеств из мощности множества n, т.е. мощности булеана этого множества.
Билет №14. Размещения данного состава и их число. Полиноминальная формула.
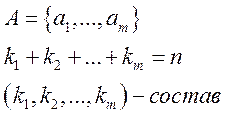
Размещением состава
![]() называется m-выборка
с повторениями в которую а1 входит ровно k1
раз,… аm входит ровно km раз.
называется m-выборка
с повторениями в которую а1 входит ровно k1
раз,… аm входит ровно km раз.
Теорема. Пусть ![]() - целые неотрицательные числа, причем
- целые неотрицательные числа, причем
![]() . Число способов, которыми можно
представить множество А из n элементов в виде суммы m подмножеств
. Число способов, которыми можно
представить множество А из n элементов в виде суммы m подмножеств ![]() число элементов
которых составляет соответственно
число элементов
которых составляет соответственно ![]() равно:
равно:
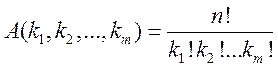
Доказательство:
Разложим множество А, состоящее
из n элементов на сумму m
подмножеств ![]() так, чтобы
так, чтобы ![]() где
где
![]() заданы, причем
заданы, причем ![]() . Последнее условие означает, что
множества
. Последнее условие означает, что
множества ![]() не должны иметь общих элементов.
не должны иметь общих элементов.
Вначале выберем k1
– элементное подмножество (существует ![]() способов
это сделать). Затем из оставшихся (n-k1)
элементов выберем k2-элементное подмножество
(число способов при этом
способов
это сделать). Затем из оставшихся (n-k1)
элементов выберем k2-элементное подмножество
(число способов при этом ![]() ) и т.д.
) и т.д.
Согласно правилу умножения общее
число способов выбрать подмножества ![]() будет:
будет:
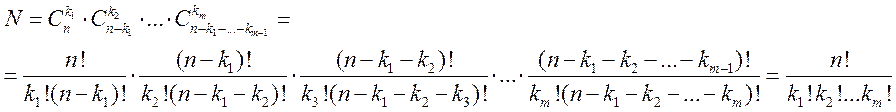
Полиноминальная формула.
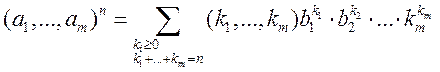
при n=2 – бином Ньютона
Пример:
найти коэффициенты при x2y3 в
выражении ![]()
m=3, n=5
k1=2, k2=3, k3=0
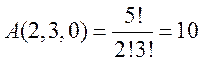
Билет №15. Сочетания с повторениями и их число.
Любое подмножество мощности r, некоторые элементы которого могут повторятся называется r-сочетаниями с повторениями из ![]() .
.
Пример:
Из элементов трех типов![]() можно составить такие сочетания с
повторениями по два элемента r=2;
можно составить такие сочетания с
повторениями по два элемента r=2; ![]()
Теорема. Число всех
r-сочетаниями с повторениями из множества ![]() , где
, где ![]() равно
равно
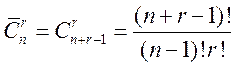 .
.
Доказательство:
Поставим в соответствие каждому сочетанию последовательность из нулей и единиц, таким образом: напишем подряд столько единиц, сколько элементов первого типа входит в сочетание, далее ставим нуль (в качестве разделителя) и затем снова напишем столько единиц, сколько элементов второго типа в сочетании и т.д., пока все типы не будут рассмотрены. Для нашего примера
aa 1100 bc 0101
ac 1001 bb 0110
ab 1010 cc 0011
Всего в каждой строке (r+n-1) символов, из них r- единиц, (n-1) – нулей. Чтобы
однозначно задать сочетание, надо задать номера мест, на которых будут стоять
нули (это можно сделать ![]() способами), или номера
мест, где будут стоять единицы (это можно сделать
способами), или номера
мест, где будут стоять единицы (это можно сделать ![]() способами).
Поэтому число сочетаний с повторениями можно вычислить по формуле
способами).
Поэтому число сочетаний с повторениями можно вычислить по формуле 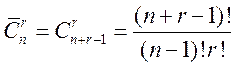 .
.
Билет №16. Задача о количестве целочисленных решений линейного уравнения.
Задача 1.
Сколько существует решений
уравнения ![]() , где xi≥0
и целое (r≥0).
, где xi≥0
и целое (r≥0).
Решение:
Каждому решению ![]() ставим в соответствие B – неупорядоченную выборку из
ставим в соответствие B – неупорядоченную выборку из ![]() такую,
что
такую,
что
а1 входит х1 раз в В
а2 входит х2 раз в В
…………..
аn входит хn раз в В
Решений существует столько,
сколько существует r-сочетаний с повторениями из
множества А, а именно ![]() .
.
Задача 2.
Сколько существует целочисленных
решений уравнения ![]() , где xi≥ai (ai – целые
числа, возможно отрицательные).
, где xi≥ai (ai – целые
числа, возможно отрицательные).
Решение:
Пусть ![]()
![]() , и пусть
, и пусть ![]()
![]()
![]() ,
где
,
где ![]() .
.
Таким образом, если
1. ![]() <0, то решений нет
<0, то решений нет
2. ![]() ≥0, то решение есть, а
именно
≥0, то решение есть, а
именно ![]()
Пример:
![]() ,
при
,
при ![]()
r= -10, n=3, s=2+(-20)+3= -15;
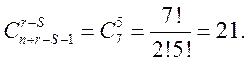
Билет №17. Формула включений и исключений и ее применение в комбинаторике.
Пусть А и В – два конечных
множества. Тогда, если ![]() , то
, то ![]() . Пусть теперь
. Пусть теперь ![]() . Тогда в
. Тогда в ![]() каждый
элемент из
каждый
элемент из ![]() будет учтен два раза. Поэтому
будет учтен два раза. Поэтому ![]() .
.
Теорема.
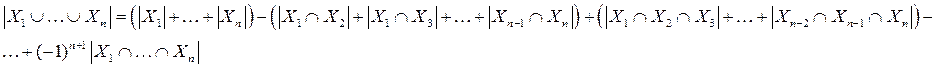 Доказательство:
Доказательство:
n=3;
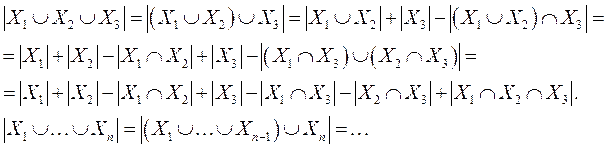
X – конечное множество, причем ![]() .
.
![]() - некоторые свойства
элементов из Х.
- некоторые свойства
элементов из Х.
![]() - множество элементов в Х,
обладающих свойством
- множество элементов в Х,
обладающих свойством ![]() .
.
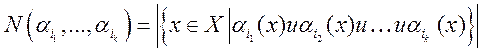 - количество элементов в Х,
обладающих одновременно свойствами
- количество элементов в Х,
обладающих одновременно свойствами ![]() .
.
![]() - количество элементов в Х,
не обладающих ни одним из свойств.
- количество элементов в Х,
не обладающих ни одним из свойств.
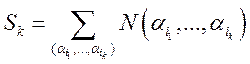
Тогда ![]() (это
равенство автоматически вытекает из второй формы записи формулы включений и
исключений).
(это
равенство автоматически вытекает из второй формы записи формулы включений и
исключений).
Пример:
n=3
![]()
Билет №18. Задача о беспорядках (применение формулы включений и исключений).
Задача:
Имеется n различных предметов a1,a2,…,an и n различных ячеек b1,b2,…,bn. Сколькими способами можно разместить предметы по ячейкам так, чтобы никакой предмет ai не попал в ячейку bi?
Решение:
В качестве исходного множества Х
возьмем совокупность всевозможных расположений предметов по ячейкам. Тогда ![]() . Введем свойства
. Введем свойства ![]() , при i=1,2,…,n. Число
, при i=1,2,…,n. Число ![]() расположений,
при которых предмет
расположений,
при которых предмет ![]() находится в ячейке
находится в ячейке ![]() ,
, ![]() =1,…,kν равно (n-k)!. Тогда
=1,…,kν равно (n-k)!. Тогда 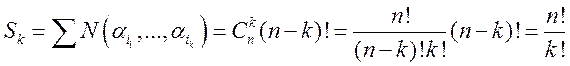
Используя теперь формулу включений и исключений, получаем, что число N0
Расположений, при которых ни одно из свойств не выполняется (т.е ни один из предметов ai не попал в ячейку bi), равно
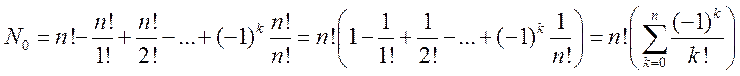
Обобщение задачи о беспорядках.
Задача.
Ровно S-элементов ![]() попали в
попали в ![]() .
Сколько существует таких распределений?
.
Сколько существует таких распределений?
Решение:
N0(S) – число таких решений.
S – неподвижных
элементов можно выбирать ![]() способами, по
правилу произведения умножаем на число беспорядков, оставшихся в n-S.
способами, по
правилу произведения умножаем на число беспорядков, оставшихся в n-S.
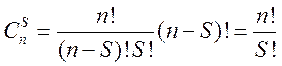 .
.
Билет №19. Изоморфизмы и автоморфизмы графов. Группа автоморфизмов графа. Примеры.
Графом будем называть совокупность двух множеств V(точек) и E(линий), между элементами которых определено отношение инцидентности.
Два графа G=(V, E) и H=(V1,
E1)называются изоморфными (G![]() H), если
существует взаимнооднозначное соответствие, т. е. биекция φ:V→V1 между
множествами их вершин, такая что
H), если
существует взаимнооднозначное соответствие, т. е. биекция φ:V→V1 между
множествами их вершин, такая что ![]() сохраняется
отношение смежности, т.е.
сохраняется
отношение смежности, т.е. ![]()
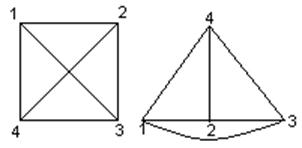 (если
вершины U и
(если
вершины U и ![]() соединены в первом графе, то их образы
будут соединены и во втором).
соединены в первом графе, то их образы
будут соединены и во втором).
Утверждение: Графы G и H изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одинаковыми перестановками строк и столбцов.
|
1 |
2 |
3 |
|
|
1 |
1 |
0 |
1 |
|
2 |
0 |
0 |
1 |
|
3 |
1 |
1 |
0 |
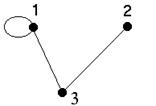
Поменяем столбцы 1 и 2, получим матрицу
|
1 |
2 |
3 |
|
|
1 |
0 |
0 |
1 |
|
2 |
0 |
1 |
1 |
|
3 |
1 |
1 |
0 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.