Билет №8. Алгебры с одной бинарной операцией: полугруппы, группы. Группа подстановок.
Отображение φ, хn→Х называется n-местной операцией. При n=2 – бинарная операция φ:х2=х×х→х
(a,b) ![]() х2, (a,b) →с
х2, (a,b) →с![]() Х
Х
Множество А вместе с заданной на
нем совокупностью операций, т.е. ![]() называется алгеброй.
называется алгеброй.
Типы алгебр:
![]() a(bc)=(ab)c
a(bc)=(ab)c
В общем случае ab≠ba, если же умножение коммутативно, то полугруппа называется коммутативной. Если полугруппа содержит такой элемент е, что для любого а ае=еа=а, то е называется единицей. Единица в полугруппе всегда единственна.
Пример:
![]() 2/3
2/3![]() N не алгебра (операция не должна выходить за рамки основного
множества.)
N не алгебра (операция не должна выходить за рамки основного
множества.)
2. Группой называется непустое множество с одной бинарной алгебраической операцией, если выполняются следующие условия:
1) ассоциативность (ab)c=a(bc)
2) ![]() ,
т.е. еа=ае=а,
,
т.е. еа=ае=а, ![]() а
а![]() А
А
3) ![]() а
а![]() А
А ![]() а-1
а-1![]() А, аа-1= а-1а=е
А, аа-1= а-1а=е
Число элементов группы называется порядком группы.
Пример группы:
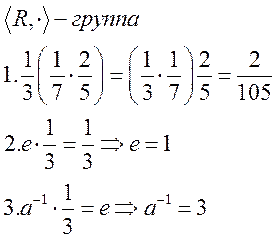
Группа подстановок.
![]()
Х – конечное множество, состоящее из n-элементов.
Взаимнооднозначное отображение Х в себя называется подстановкой.
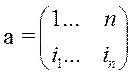 , Sn-
множество всех подстановок
, Sn-
множество всех подстановок
![]()
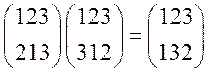
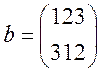 ;
; 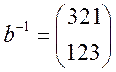
(ab)c=a(bc)
Билет №9. Алгебры с двумя бинарными операциями: кольца, поля. Примеры колец и полей.
Алгебра ![]() с
двумя бинарными операциями называется кольцом, если
с
двумя бинарными операциями называется кольцом, если
1. ![]() коммутативная группа
коммутативная группа
2. ![]() полугруппа
полугруппа
![]() 3. a(b+c)=ab+ac
3. a(b+c)=ab+ac
(b+c)a=ba+ca дистрибутивность
Пример:
![]()
1. ![]()
1+2=2+1
2. ![]()
(1*2)*3=1*(2*3)
3. 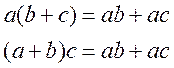
![]() является кольцом.
является кольцом.
Алгебра ![]() называется
полем, если
называется
полем, если
1. ![]() коммутативная группа с
единицей
коммутативная группа с
единицей
2. ![]() коммутативная группа
коммутативная группа
3. a(b+c)=ab+ac
Пример:
![]() -
поле?
-
поле?
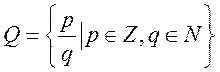
1.
1.1. 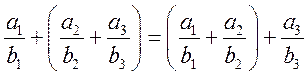
1.2. е=0
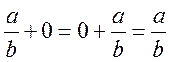
1.3.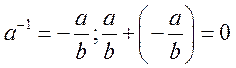
2.
2.1 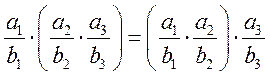
2.2 е=1 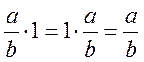
2.3 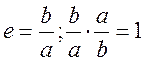
3. 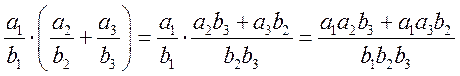 ;;
;;
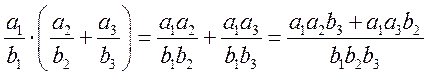
![]() является
полем
является
полем
Билет №10. Изоморфизмы и автоморфизмы алгебр. Примеры.
Две алгебры ![]() и
и ![]() называются
изоморфными, если существует биекция U:А→В
такая, что
называются
изоморфными, если существует биекция U:А→В
такая, что
1. U – взаимнооднозначна
2. U(ab)=U(a)*U(b), ![]() a,b
a,b![]() A,B(биекция сохраняет операцию).
A,B(биекция сохраняет операцию).
Свойства изоморфизма:
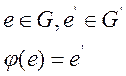
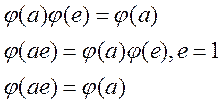
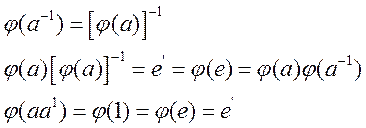
3. обратное отображение ![]() :G’→G, также является изоморфизмом.
:G’→G, также является изоморфизмом.
Пример:
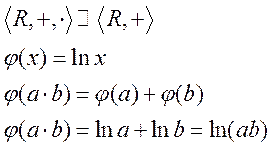
обратное отображение
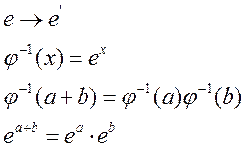
Определение: ![]() существует биекция
существует биекция ![]()
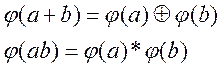 , +→
, +→![]() ,
,
![]() →*
→*
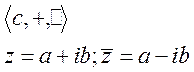
сопряжение – биекция с→с
Изоморфизм алгебры на себя называется автоморфизмом.
![]()
нужно показать, что
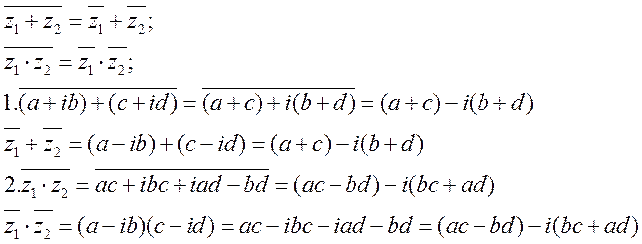
Билет №11. Системы линейных уравнений и многочлены над кольцом вычетов по модулю m.
Теорема 1. Если
число ![]() корень многочлена f=anxn+…+a1x+a0 с действительными
коэффициентами ai, то
корень многочлена f=anxn+…+a1x+a0 с действительными
коэффициентами ai, то ![]() тоже корень многочлена f(x).
тоже корень многочлена f(x).
Доказательство:
n=2; f(x)=ax2+bx+c
Подставим в многочлен вместо х число z, получим:
![]() , где M
и N – выражения не содержащие i,
т.к.
, где M
и N – выражения не содержащие i,
т.к. ![]() - корень многочлена, то
- корень многочлена, то ![]() , откуда
, откуда ![]() .
.
Теперь подставим в многочлен
вместо х выражение ![]() . Тогда получим число
сопряженное с числом
. Тогда получим число
сопряженное с числом ![]() , т.е.
, т.е. ![]() . Т.к.
. Т.к. ![]() ,
то
,
то ![]()
![]() тоже
корень уравнения.
тоже
корень уравнения.
Теорема 2. Любой многочлен нечетной степени с действительными коэффициентами имеет хотя бы один действительный корень.
Доказательство:
n=3; ![]() корень
f(x)
корень
f(x)
по теореме (1) ![]() тоже корень f(x)
тоже корень f(x)
![]() третий корень
действительный.
третий корень
действительный.
Кольцо вычетов.
n – фиксированное число
Два целых числа n,n’ называются сравнимыми по ![]() , если при делении на m они дают одинаковые остатки.
, если при делении на m они дают одинаковые остатки.
![]() >1
>1
![]() ,
m-модуль сравнения.
,
m-модуль сравнения.
m=2
1=3=5=7=9=11 (mod 2)
0=2=4=6=8=10 (mod 2)
![]()
![]()
Тогда множество разбивается на классы чисел, сравнимых между собой по модулю m и называются они классы вычетов по модулю m. Каждый класс имеет вид:
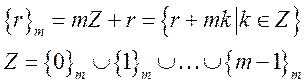
по определению n и n’ сравнимы по (mod m)
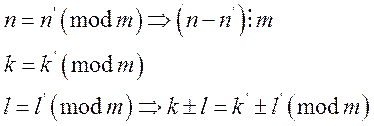
![]()
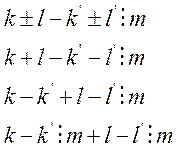
Каждым двум классам ![]() и
и ![]() можно
сопоставить класс, который является их суммой или произведением.
можно
сопоставить класс, который является их суммой или произведением.
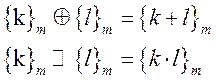
Свойство: если два числа сравнимы по некоторому модулю, то все их натуральные степени также сравнимы по этому модудю.
Утверждение: Если n-простое число, то кольцо вычетов ![]() поле,
т.е ненулевые элементы образуют группу.
поле,
т.е ненулевые элементы образуют группу.
![]() - группа
- группа
Если кольцо вычетов Zn является полем, т.е. Zn – простое число, то большинство утверждений для объектов с действительными коэффициентами справедливо и для объектов с коэффициентами из этого поля вычетов.
Билет №12. Выборки с повторениями и без повторений, перестановки. Их число.
r -
выборкой из множества А=![]() называется набор
называется набор
![]() элементов из А длины r.
элементов из А длины r.
r-выборка называется упорядоченной, если в ней задан порядок следования элементов
|
|
|||
|
упорядоченные |
неупорядоченные |
||
|
Размещения без повторений |
Размещения с повторениями |
Сочетания без повторений |
Сочетания с повторениями |
1. r – выборки с повторениями это упорядоченные r-выборки, элементы которых могут повторятся.
nr
– число всех r-выборок из множества А=![]() .
.
![]()
![]()
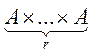
![]()
Пример:
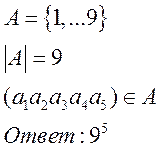
2. Если элементы упорядоченной r-выборки попарно различны, то она называетсяr – выборкой без повторений
Теорема. Число всех
упорядоченных подмножеств из множества А без повторений равно 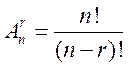 .
.
Доказательство:
Будем последовательно выбирать элементы множества А и размещать их в определенном порядке на r местах. На первое место можно поставить любой из n элементов А. На второе место можно поставить любой из (n-1) оставшихся элементов А и т.д. На r место можно поставить (n-r+1) элемент. По правилу умножения (Если A и B - конечные множества и | A | = m, | B | = n, то мощность множества A x B равна m x n) получаем:
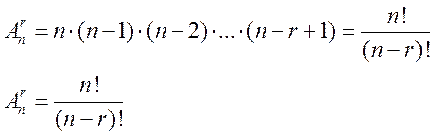
Пример:
Сколькими способами можно рассадить 5 студентов за 10-ю столами(по одному за стол)?
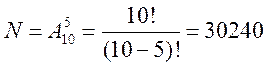 .
.
3. Перестановки.
Различные n-элементные множества, которые отличаются лишь порядком элементов(т.е. могут быть получены из того же самого множества) называются перестановками этого множества. Перестановки отличаются лишь порядком следования элементов. Состав элементов не важен. Всякое множество можно упорядочить. Множество, содержащее более одного элемента можно упорядочить не единственным способом. Найдем число этих способов.
Теорема. Число
перестановок n-элементного множества равно ![]() (это r-выборка
без повторений при n=r, т.е.
(это r-выборка
без повторений при n=r, т.е. ![]() ).
).
Доказательство:
Число перестановок вычисляется по правилу
произведения (если объект a может быть выбран m способами, и
после этого объект b может быть выбран n способами, то выбор пары
(a, b) может осуществляться m x n способами). Будем
последовательно выбирать элементы множества А и располагать их в определенном
порядке на n местах. На первое место можно поставить
любой из n элементов. На второе
место выбираем любой из (n-1) оставшихся элементов и
т.д. на последнее n-ое место у нас останется один
элемент. По правилу умножения все n мест можно
заполнить ![]() числом способов.
числом способов.
Пример:
Сколькими способами можно
расставить на полке 4 книги?
N=P4 = 4!=24
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.