Метод узловых потенциалов

Существует много методов получения ММС. Мы будем изучать 2 метода: 1-й – метод переменных состояний (МПС) и 2-й – метод узловых потенциалов (МУП).

Метод узловых потенциалов

Особенности цепи

1. 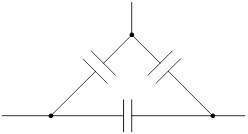 Замкнутые контура, состоящие только из источников напряжения и емкостных элементов.
В схеме появляются емкостные хорды и должны быть применены сложные алгоритмы анализа (емкости и источники напряжения в обычных схемах – всегда ребра).

2. 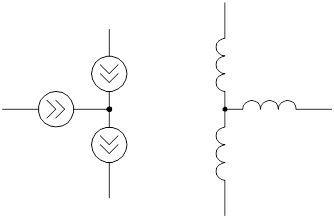 Индуктивные (источники тока) звезды, т.е. узлы, к которым подключены только индуктивности или только источники тока. Обычно такого рода особенности являются ошибками проектировщика.
Индуктивности и источники тока обычно являются хордами. В этом же случае появляются индуктивные ребра или ребра из источников тока, что приводит к тем же последствиям, что и в первом случае, т.е. к усложнению программ и алгоритмов анализа.
Мы будем изучать схемы без особенностей.

Уравнение RLC-цепи без особенностей

В схеме можно выделить группы элементов:

1.  Источники воздействия (E, I).

2.  R-цепь – пассивная линейная резистивная цепь.

3.  Реактивные элементы L и C.

Резистивная цепь находится под воздействием источников 2-х типов: реальные (E, I) и L, C, от которых можно перейти к источникам замещения.

1.  Источники воздействия представляют собой векторы воздействия .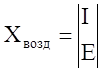

2.  Источники замещения реактивных элементов, представляемые вектором состояния .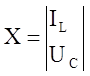

Таким образом, ток в резистивной цепи записывается:

                          (11)     Уравнение токов резисторов.

В₁ и В₂ получаются из матрицы главных сечений,

_Xвозд     – известная величина,

Х         – является переменной (вектор состояния).

Значит, I_рез нельзя определить, т.к. в каждом уравнении содержится 2 переменных

           

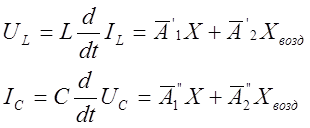
Разрешим эти уравнения относительно производных и запишем их в одно матричное уравнение

Произв вект. сост 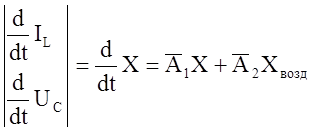                         (12)             Уравнение состояния

1.  Порядок системы дифференциальных уравнений равен числу реактивных элементов схемы.

2.  В цепи без особенностей все реактивные элементы имеют нулевые начальные условия.

Система из уравнений (11) и (12) является полной системой, т.е. из нее могут быть найдены все переменные.

Из уравнений (12) может быть найден вектор состояний для анализируемого момента времени. Подставив Х в уравнение (11), найдем токи в резисторах I_рез на тот же момент времени.

Уравнения 11 и 12 являются ММС, полученной по МПС.

Топологический метод получения матриц А и В

Матрица         [B1] – (число резисторов х число реактивных элементов)

[B2] – (число резисторов х число источников E, I).

Используя правило построения топологических уравнений с помощью МГС

                                   (13) Уравнение токов ребер

                    (14) Уравнение напряжений хорд.

Дополним эти уравнения компонентными:

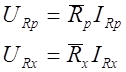                  (15)  – матрицы сопротивлений ребер и хорд

(имеют в диагоналях сопротивления соотв. резисторов, остальные элементы – 0)

Подставим (15) в 13 и 14

Матричное представление

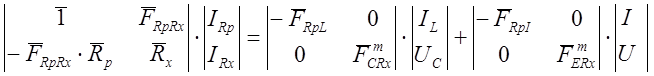            (16)

Сокращенно

 (17)    =>  ;     ;

Получили коэффициенты А₁ и А₂ в уравнениях состояний для этого запишем токовые уравнения напряжений в индуктивностях и токов в емкостях.

                    (19)

                             (20)

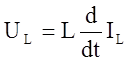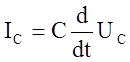;                ;             (21)

Подставим (21) в 19,20 и выразим U_Rp через I_Rp .

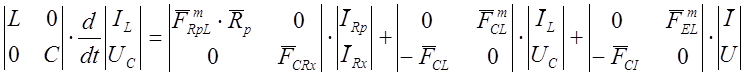
Сокращенно

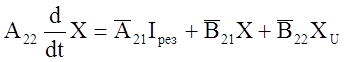
Подставим I_рез из ур-я (11).  Разрешим уравнение относительно , с учетом (12) получим

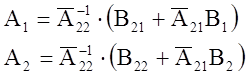                     (23)

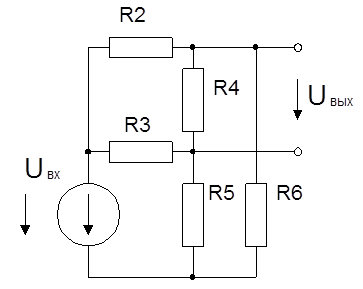
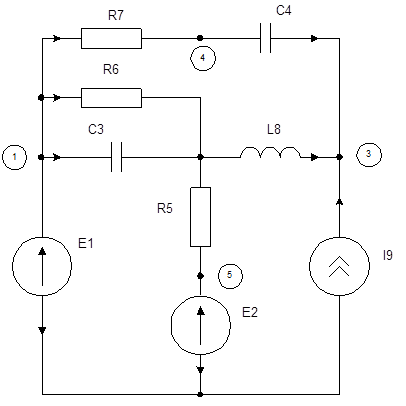Схема

R5 = 100 Ом                 L8 = 2 mГн

R6 = 10 k                       C3 = 500 пФ

R7 = 20 k                       C4 = 10 нФ

M_R = 10³            M_C = 10^-9

M_L = 10^-3

;            ;

;            ;            ;

;

  =>   ;

;        ;                 ;

  =>   ;              ;

;        ;

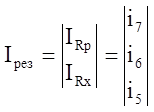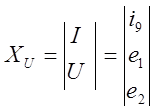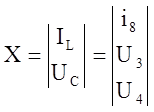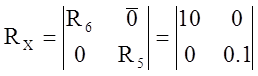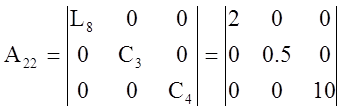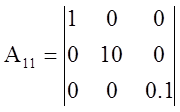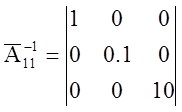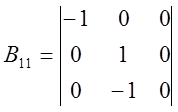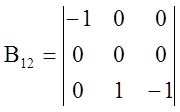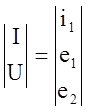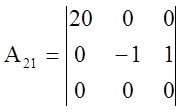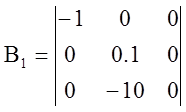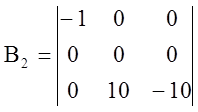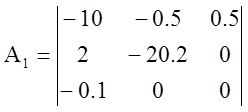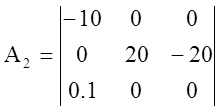Запишем ММСх, полученную методом переменных состояний

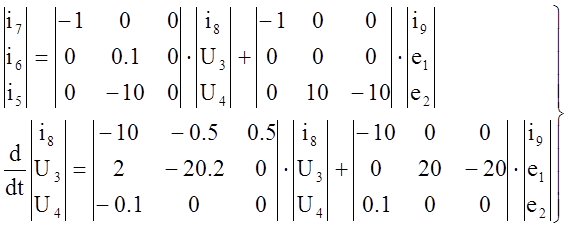    MMC

Расчет характеристик линейной цепи

Кроме токов и напряжений на элементах схемы разработчиков интересуют и другие параметры разрабатываемой схемы. Большое значение имеют отношения напряжений и токов в различных точках, характеризующие передаточные свойства цепи.

В схеме выделяют характерные точки, называемые входом и выходом. Ко входу подключают источник, называемый входным воздействием (X_вх) и изучают X_вых, (ток или напряжение), т.е. отклик цепи.

Коэффициентом передачи  называется отношение 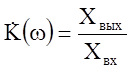; при X_вх =1 ,                   где        – АЧХ,           

                                                    – ФЧХ, 

Переходная характеристика  h(t) есть отклик на единичный скачок  X_вх(t) = 1(t), начальные условия  X(0) = 0.           При t=0 ток в индуктивных элементах и напряжение на конденсаторах = 0,  т.е. схема не содержит запасенной энергии.

Импульсная характеристика представляет собой g(t) на единичный импульс
[X_вх(t) = d(t)]. Начальные условия также нулевые.

Любая из этих характеристик описывает свойства цепи. Зависимость между характеристиками определяется выражениями:

Частотная и импульсная характеристика

;                                            

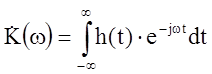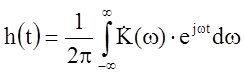
Импульсная и переходная характеристика

;                          

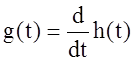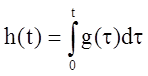
Примечание:    Коэффициент передачи может быть безразмерной величиной или иметь размерность R [Ом] или g [сим].

K(w) – действительна, если отсутствуют реактивные элементы.

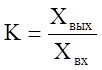Коэффициент передачи резистивной цепи

          – коэффициент передачи.

Вспомним уравнение

В схеме выделяют только один источник воздействия, все остальные убирают (I – разрыв, U – КЗ).

X=0;      (отсутствуют реактивные элементы).

A×I_рез = B×X_возд              (43)

Уравнение отклика цепи

,             D₁ – вектор, D₂ – коэффициенты                (44)

Пример:  Найдем коэффициенты D₁  и D₂, если входное воздействие – напряжение.

,

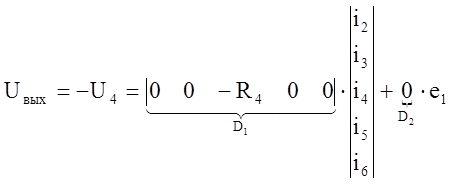или

;

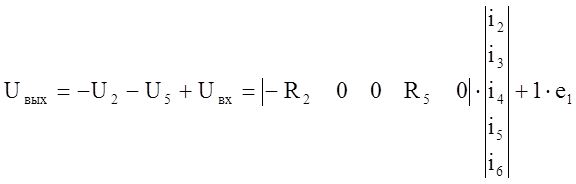Найдем выражение для передаточной функции резистивной цепи в общем виде. Для этого подставим I_рез  из (43) в (44).

     

                                 (45)

В случае выбора других точек выхода в уравнение подставляются другие значения коэффициентов D₁ и D₂. А в случае выбора других точек входа подставляются другие значения B.

Передаточная функция RLC-цепи

Под передаточной функцией RLC-цепи понимается выражение 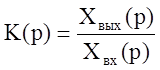 изображения в плоскости p можно записать в показательной форме

или в дробно-рациональной форме, числителем и знаменателем которой являются полиномы p.

.

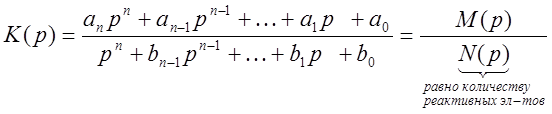n -  порядок анализируемой цепи.

Найдем передаточную функцию RLC-цепи из выражения

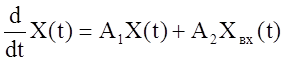;                          (47)     уравнение состояний

;                          (48)     уравнение отклика цепи

Запишем эти уравнения их изображениями по Лапласу.

;                   (49)