Метод узловых потенциалов, страница 4

            Пакетов производящих оптимизацию параметров мало. Выборы критериев во многом субъективны. При этом ориентируются на эталонные образцы, экспертные оценки и техническое задание.

            Эталонные – передовые изделия в данной области.

            Экспертные – субъективная оценка свойств.

Некоторые внутренние параметры не могут быть изменены в процессе оптимизации.

Постановка задачи оптимизации.

1. Нужно поставить задачу оптимизации.

2. Решение задачи оптимизации, имеющей математическую формулировку.

Задачи найти экстремум , где  - вектор внутренних параметров.

            Постановка задачи

1. Выбор критерия оптимальности и варьируемых параметров.

2. Назначение ограничений.

3. Нормирование управляемых и выходных параметров.

            Выбор целевой функции (критерия оптимальности)

Трудности:                а) целевая функция носит векторный характер (многофакторность)

                                    б) конфликтность параметров (один, другой)

            По принципу однозначности критерий оптимальности должен быть один. Объединение нескольких параметров в один критерий оптимальности называют сверткой векторного критерия нахождения функции .

            Теперь нужно найти экстремум функции  одним из математических методов программирования.

            В зависимости от того, каким образом выбираются и объединяются параметры, скалярные критерии оптимальности, различают различные критерии:

1. Частный критерий. Применяется в тех случаях, когда среди выходных параметров можно выделить один основной, наиболее полно отражающий эффективность проектируемого устройства. Это параметр и принимают за целевую функцию. Остальные параметры в этом случае переводятся в ряд ограничений.

            Достоинства – простота.

            Недостаток – запас работоспособности получают по одному параметру.

2. Взвешенный аддитивный критерий. Применяется тогда, когда можно выделить две группы выходных параметров. В первую группу входят те, которые в процессе оптимизации надо увеличивать, а во вторую, те которые надо уменьшать. , .

Критерий оптимальности будет таким:

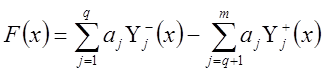
 - весовые коэффициенты, определяющие степень важности j – го параметра.

3. Мультипликативный критерий.

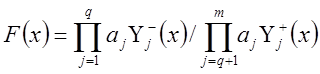
4. Критерий формы функций. Используется в случае, если необходимо обеспечить наилучшее совпадение эталонной заданной характеристики  с соответствующей выходной характеристикой - проектируемого устройства.

ω – некоторая переменная величина          (АЧХ, ПХ, ФХ)

Используется в настройке тел. ВМ приемников и других устройств для соответствия характеристик заданным

            Для формирования критерия оптимальности введем понятие отклонения в j-ой точке. В этом случае минимизации подлежит одна из целевых функций 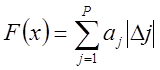, где -сте-

пень значимости отклонений. -т.е. берут максимальное отклонение и сведем его к минимуму.

5. Минимальные методы. Имеют хорошо разработанный математический аппарат и очень широко применяется во всех отраслях. Минимальный максимизируется из из показателей качества

                        Назначение ограничений.

            Ограничения появляются объективно и вытекают из конкретной физической и технологической реализуемости параметров. Они сужают область поиска допустимого решения и искомый экстремум целевой функции становится условным.

            Ограничения формируют допустимую область поиска решения (область работоспособности устройства).

                        Нормирование управляемых и выходных параметров.

            Необходимо, чтобы все параметры имели одинаковую размерность или являлись безразмерными. Виды нормировки:

1. С помощью весовых коэффициентов.      

2. 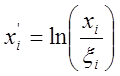        где-коэффициент численно равный единице параметра.

                        Математическая формулировка задачи оптимизации.

            Наиболее типичным случаем параметрической оптимизации устройств является поиск значения вектора управляемых внутренних параметров составляющих экстремум целевой функции.               -при наличие ограничений.

Моделирование полупроводниковых приборов.

            Описание электрических свойств полупроводниковых приборов с помощью эквивалентных схем, мат. уравнений – это моделирование.

            Чаще всего мод. в САПР происходит моделирование с помощью эквивалентных схем. Большинство САПР имеют встроенные модели, для которых создана библиотека стандартных элементов.

Математическая модель по методу МПС для цепей с

управляемыми источниками

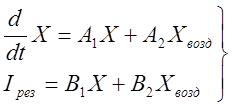              ММС по МПС

В векторе Х_воз появляются зависимые источники тока и напряжения и т.к. они зависят от напряжений и токов в других ветвях они должны быть выражены через токи резистивных ветвей или через элементы вектора Х и в последующем устранены из математической модели.

Рассмотрим на примере простейшего усилителя:

                                    

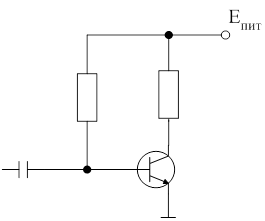
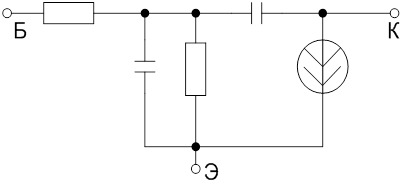
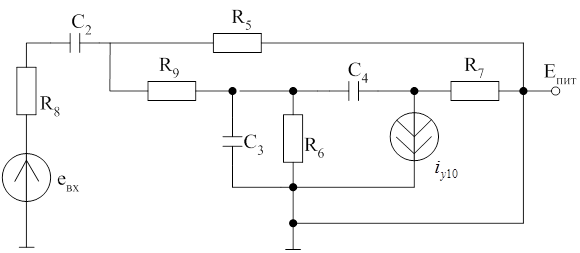
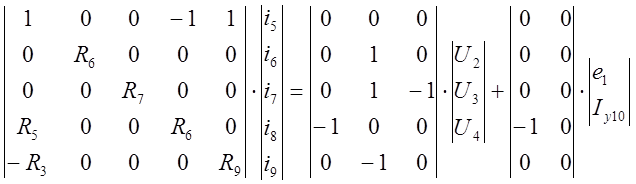
             А₁₁                         I_рез          В₁₁            Х         В₁₂       Х_воз

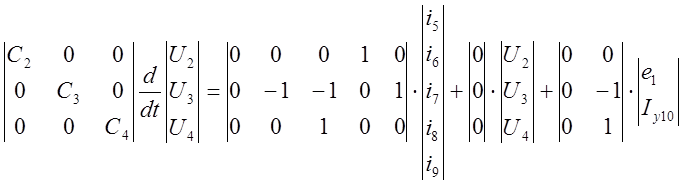
      А₂₂                                  А₂₁                   I_рез  В₂₁    Х       В₂₂       Х_воз

1) Переменной  в В₁₂ и В₂₂ принадлежат последние столбцы т.к. в матрице В₁₂ этот столбец лишь в первом столбце собственно переменная  из него может быть исключена.

2) Во втором уравнении заменим  можно на место  в Х_воз списать U₃, умножив элементы второго столбца на .

3). В правой части U₃ встречается в обоих членах уравнения, приведем подобные члены. Для этого прибавим элементы столбца В₂₁ к соответствующему столбцу матрицы В₂₁.

            Можно сделать по-другому

Аналогично вышесказанному умножим второй столбец В₂₂ на , подставим в Х_воз на место у_i y₆ при этом в правой части переменная оказывается в 2^х частях. Перенесем  во второй столбец А_21.

            При необходимости исключение переменных токов резисторов осуществляем аналогичным образом.

Анализ цепей с большим разбросом параметров.

            В анализизируемой схеме могут содержаться реактивные элементы, параметры которых отличаются на несколько порядков. Нахождение характеристик (АЧХ, ФЧХ), в этом случае сильно затрудняется, а часто и невозможно.

            При анализе таких схем формируют различные эквивалентные схемы с учетом диапазона частот НЧ, ВЧ, СЧ. Получают разные схемы и анализируют их по отдельности.

            Элементы разбивают на группы с малыми, средними и большими параметрами. В области ВЧ малы напряжения на емкостных элементах с большими и средними параметрами (мало их сопротивление ВЧ) и малы токи в индуктивных элементах (т.е. велико их сопротивление). Также поступают с СЧ и НЧ.

            На НЧ откл. С и закорочены L с малыми и средними значениями параметров.

                                                                            

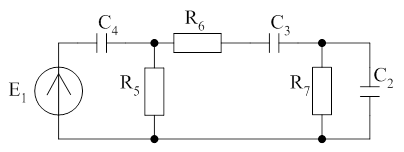
            Пример:

С₄=10мкФ

С₃=10нФ

С₂=10pФ

ВЧ

СЧ

НЧ