Информатика и выч. техника \ Основы комплексного проектирования и моделирования радиоэлектронных систем

Метод узловых потенциалов, страница 2

;           (50)

Решаем эти уравнения относительно X(p).

;

;

Подставляя X(p) в (50), получим

;

Тогда выражение для передаточной функции RLC-цепи имеет вид

                     (51)

Основная трудность вычисления заключается в нахождении обратной матрицы .  Рассмотрим метод вычисления такой матрицы, называемый методом Лаверрье-Фаддеева.

Если имеется квадратная матрица (матрица А), то с помощью этого метода можно найти ее различные характеристики:

1.  Характеристический многочлен матрицы n-го порядка

Корни этого многочлена называются собственными значениями матрицы.

2.  Дробно-рациональная форма представления обратной матрицы

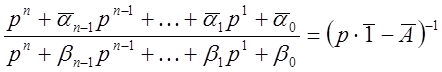
 – матричные коэффициенты такого же порядка, как и матрицы А.
Принимаем  и . Проводят вычисления:


Т.о. находим матричные коэффициенты a, b, B.
Выражение (*) позволяет проверить правильность произведенных вычислений.

3.  Обратная матрица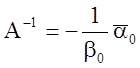      

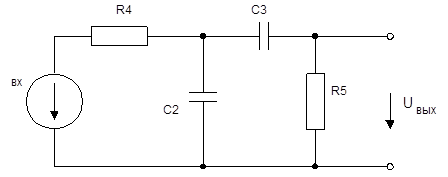Пример:        Имеем цепь 2-го порядка

С2 = 0.5 нФ,

С3 = 0.25 нФ,

R4 = R5 = 2 кОм

Найдем выражение для передаточной функции:

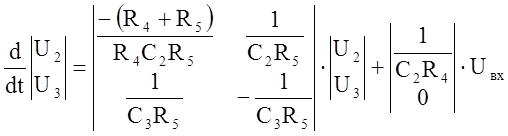
Подставим параметры элементов

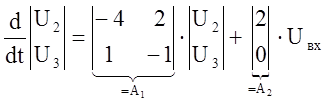
Запишем для этой же схемы уравнения токов резисторов

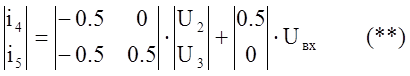
Выражение для отклика цепи:

;

.

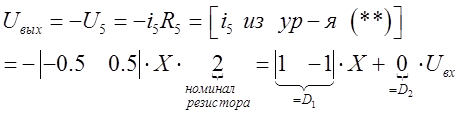
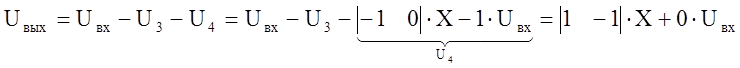С учетом найденных коэффициентов D1 и D2 уравнение отклика имеет вид

;

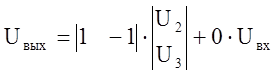Произведем вычисления над матрицей A1 по схеме Лаверрье-Фаддеева (чтобы найти передаточную функцию).

Матричные вспомогательные коэффициенты

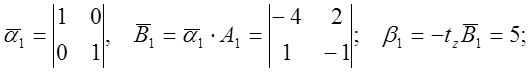
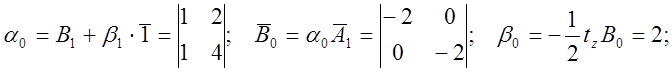
Получили все коэффициенты.

;

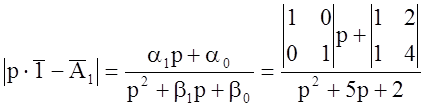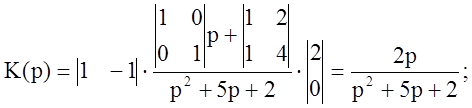
            Выражение для передаточной функции к 5 лаб. работе.

Учет многополюсников при формировании М.М.С. по методу Узловых Потенциалов.

Многополюсники полностью характеризуются соотношениями между токами и напряжениями на его входах.

 Ч.П. с двумя парами зажимов может быть описан с помощью нескольких параметров. М.М. Ч.П. (не нагруженного) с 2-мя парами зажимов может быть определена в матричной форме следующим образом:

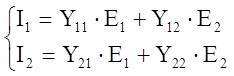    (120)      В матричной форме  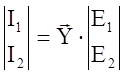 где Y= 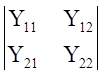                    I,E – комплексная амплитуда (sin при ω=const).

Из системы (120) найдем проводимости.

        

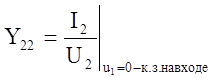
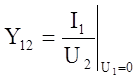  проводимость обратной передачи при к.з. на входе.

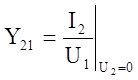   проводимость прямой передачи при к.з. на выходе.

Характеристика влияния входного напряжения на выходной ток.

Такое представление многополюсников в виде элементов с парами зажимов является неудобным для использования в САПР. Поэтому перейдем от Ч.П. с 2-параметрами контактов (зажимов) к модели многополюсника с 4-полюсами.

Преобразуем Ч.П. в 3-полюсник и посмотрим, как это отразится на

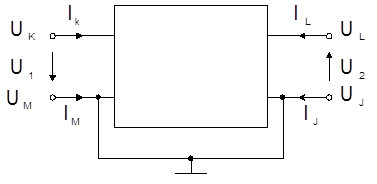U1 = UK - UM            IK = I1             IL = I2               (124)

U2 = UL - UI             IM = -I1           II = -I2

Основное уравнение Ч.П. 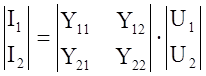             (125)

Следовательно:

Подставим U1 и U2 из (124).

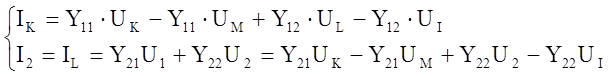
M.M. Ч.П. где IK = -IM и IL = -II. Учтем, что обычно выводы М и I обычно объединяются. Кроме того, они, как правило, оба заземляются. Тогда имеем:      - ток через узел M'.

Приведем подобные в предыдущих уравнениях токов и получаем M.M. Ч.П.:

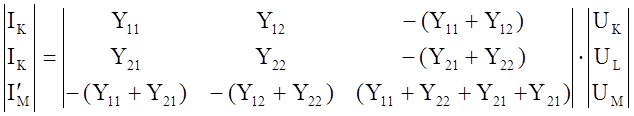  Уравнение перехода от Ч.П. к 3-х П.


В эл. схемах могут существовать многополюсники т.е. имеем n-выводов:

Матрица полюсных проводимостей имеет размерность (n-1)х(n-1).

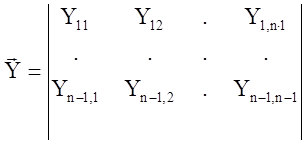
Для нахождения параметров матрицы Y.

1)  Все выводы М.П., кроме одного, заземляют. К оставшемуся j-выводу подключают ист. напряжения. В этом случае в матрице полюсных проводимостей Y остается лишь j-столбец, а в векторе источников напряжения только Uj.

Система уравнений имеет вид:   где  i=1,n-1.

2)  Измеряют токи во всех ветвях, и находим элементы столбца по формуле: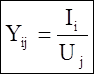

3)  Далее измерения проводим при подключении источника к другому полюсу и так до заполнения матрицы Y.

Вектор токов находится заземлением всех полюсов многополюсника. Если в векторе тока есть ненулевые элементы, то в нем содержатся независимые источники напряжения и тока.

Для описания многополюсников с использованием М.У.П. наиболее удобно использование Y-параметров.

Эти матрицы объединяются простым суммированием

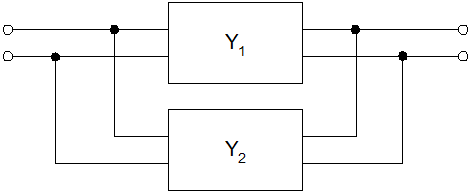элементов.

При составлении по М.У.П. М.М.С. содержит

многополюсники, элементы матрицы Тс=

полюсных проводимостей помещают в со-

ответствующие позиции матрицы узловых проводимостей схемы, алгебраически суммируясь с содержимым этих позиций.

Y=Y1+Y2

Элементы вектора полюсных токов также алгебраически суммируя с соответствующими элементами вектора токов схемы. 

Расчет частотных характеристик с использованием

передаточной функции

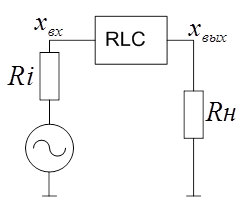            Если цепь линейная и на вход подан сигнал с частотой ω, то и на выходе будет сигнал с той же частотой. Изменяется только амплитуда сигнала. Четырехполюсник определяется передаточной функцией при замене переменной в передаточной функции на jω.

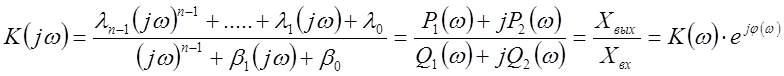
где - АЧХ;  - ФЧХ

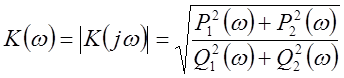                                                  (55)

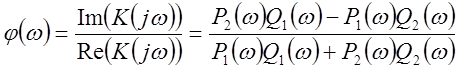                               (56)

Коэффициенты  и  получают из выражения передаточной функции цепи:

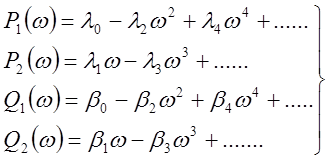                                                    (53)

            Если имеем математическое выражение для П.Ф. для того чтобы найти АЧХ и ФЧХ необходимо:

            1. Выбрать ряд частот, где надо найти АЧХ и ФЧХ.

            2. Поставив эти частоты в (53) находим  и .

            3. Подставив найденные значения в (55) и (56) получаем значения АЧХ и ФЧХ в данной точке.

Расчет АЧХ с использованием уравнения состояния.

            уравнение состояния:

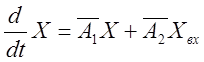                                        (47)

            уравнение отклика:

                                       (48)

            Если воздействие гармоническое то все переменные комплексные

                                      (57)

                                      (58)

            При ; :

                                             (59)

                                            (60)

Комплексную переменную представим в виде ;

            Приравнивая действительные и мнимые части уравнений (59) и (60) получим следующую систему:

                                  

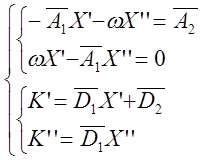
            Решая систему уравнений (61), (62) на каждой новой частоте, в которой находятся значения  и . Подставляя эти значения в (63) и (64) находим значения  и . Из них рассчитываем значения АЧХ и ФЧХ в конкретных точках.

                                                

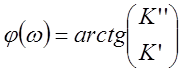
            Для нового значения частоты все операции повторяются. Недостатком этого метода является большой объем вычислений. Данный метод применяется, когда АЧХ и ФЧХ нужно найти в малом числе отсчетов частоты. Этот метод применяется, если затруднительно или невозможно получить передаточную функцию.  трудно найти при большом разбросе постоянных времени цепи.

            Как правило в программах САПР нахождение ЧХ производится в точках выбираемых по формуле:

                                  

Скачать файл