Метод узловых потенциалов, страница 3

при  и , шаг получается равномерным. Для логарифмической шкалы необходимо выбрать  и .

Анализ чувствительности схемы к отношению

параметров элементов.

Анализ схемы – это нахождение вектора ее выходных параметров

                   

Любая схема обладает внутренними параметрами

                   

В общем случае каждый из параметров  зависит от параметров

                    

            Номиналы элементов схемы всегда отличаются от рассчитанных: разброс номиналов R, C, токов утечки паразитных емкостей , разброс характеристик полупроводниковых приборов(транзисторы, ОУ).

            Под влиянием внешних факторов: температура, давление, влажность и т.д. вектор  изменяется и как следствие изменяется вектор выходных параметров . При анализе пригодности схемы или устройства в целом к эксплуатации оценивают вектор выходных параметров  на соответствии ее допускам

                         

            Если  выходит за указанные допуски, то устройство считается неработоспособным. Чтобы снизить затраты на настройку устройства и увеличить «выход годных» применяют моделирование схем с разбросом параметров схемы .

            При анализе чувствительности схемы к разбросу параметров элементов основной задачей является оценить степень влияния изменения  на .

            Чувствительность схемы к изменениям внутренних параметров – это реакция схемы на малое изменение ее внутренних параметров. Для численной оценки чувствительности введем коэффициент чувствительности – это количественная оценка изменения выходного параметра  при заданном изменении параметра Х.

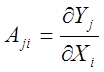                -    коэффициент влияния  на .

            Чаще всего при анализе чувствительности решают следующие задачи:

1.  Нужно выявить внутренние параметры, к изменению которых наиболее чувствительна  схема.

2.  Найти вероятность того, что при изменении в заданных пределах внутренних параметров устройство будет работоспособным.

3.  При изготовлении устройств всегда присутствуют паразитные элементы. Нужно вести анализ наличия паразитных элементов.

4.  Старение элементов.

5.  Сравнение различных устройств, обладающих одинаковыми характеристиками кроме коэффициента чувствительности

            Если анализируется устройство с m – выходными и n – внутренними, тогда для него необходимо найти матрицу коэффициента чувствительности.

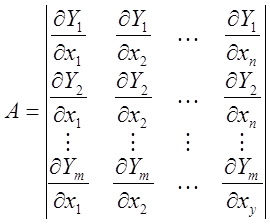
            Каждая j-строка этой матрицы является вектором-градиентом j-выходного параметра  в пространстве внутренних параметров Х, каждый i-столбец характеризует влияние i-того внутреннего параметра на все выходные параметры Y.

            Чаще всего невозможно найти аналитическое выражение зависимости , поэтому для нахождения используют различные численные методы.

             имеет размерность х-(Ф, Ом, Гн), у-(В, Гц, и т.д.).

Значит можно сравнивать только чувствительности у однотипных элементов.

            Для практической оценки используют чувствительность

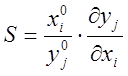,         где  - номинальные значения

Чувствительность – численно равна относительному отклонению характеристики , вызванному единичным отклонением параметров . Эта величина безразмерная и можно легко сравнивать влияние всех элементов на выходные характеристики.

Алгоритмы нахождения коэффициентов чувствительности.

Метод приращений (в курсовом).

; 

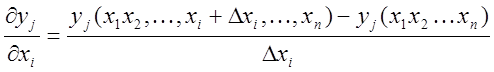где  - с приращением,  - номинальная характеристика.

            Алгоритм:

1. Произведём расчёты выходных параметров в номинальном режиме, т. е. найдём .

2. Производят расчёты n-случаев, в каждом из которых приращение  даётся только одному из внутренних параметров.

3. Найдем соответствующие коэффициенты чувствительности.

            Недостатки:

1. Большой объем вычислений  раз.

2. Формула  предполагает линейную зависимость Y от Х. Но на самом деле это редко выполняется т.к.  - нелинейная.

            Два способа повышения точности расчета:

1. Находим  при отклонении Х в обе стороны от номинального значения, тогда

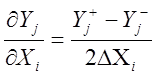                    но для этого схему нужно анализировать  раз.

2. Уменьшение , однако это приводит к существенному увеличению  машинных затрат, прежде всего из-за уменьшения шага интегрирования(при решении систем уравнений).

Общая характеристика метода малых приращений.

            Преимущества:

1. Крайняя простота.

2. Можно найти   от  .

3. Можно сделать распараллеливание вычислительного процесса. Считая, что приемлемая точность обеспечиваемая при  т.е. 25%

Метод синтеза по наихудшему сочетанию параметров

 элементов.

            Всем параметрам элементов схемы дают максимальное по величине и такое по знаку приращение, при которых возникают наибольшее по абсолютному значению отклонения выходного параметра.

            Недостаток:

Этот метод дает слишком пессимистические прогнозы(оценки) и при таких внутренних параметрах устройство оказывается неработоспособным т.е. .

            Достоинства:

1. Если все же устройство оказывается работоспособным, то оно имеет очень маленькую чувствительность к разбросу и считается хорошо разработанным.

2. Малое количество расчетов.

Метод моментов.

            Применяется тогда, когда между отклонениями параметров элементов существует сильная корреляция (связь). Например в ИМС.

            Для использования этого метода должны быть известны статические характеристики параметров элементов: распределения, дисперсия и т.п.

            Если эти характеристики известны, то для вычислений могут быть применены стандартные библиотеки типовых программ: вычисления определенного интеграла, расчета статических характеристик, далее по известным методикам находят коэффициенты чувствительности схем.

Анализ влияния разброса параметров методом Монте–Карло

(метод статистических испытаний).

            Проводят N–испытаний схемы. Для каждого элемента с варьируемым параметром ЭВМ формируют последовательность случайных чисел. Каждая последовательность случайных чисел имеет те-же распределения и корреляционные связи с другими параметрами, какими обладает параметр, который представляет эти случайные числа.

            В каждом из N – истинный параметр схемы приобретает случайный набор значений с соответствующими законами. Производится анализ схемы, потом генерируются новые значения параметров и опять производим анализ схемы. При одних схема может быть работоспособна, при других нет. Произведя достаточно большое количество испытаний можно определить требуемые характеристики схемы. Например:

1. Найти относительное число случаев, когда выходные параметры удовлетворяют требованиям. Это и есть проценты выхода годных и брака.

2. Можно проанализировать причины брака по каждому из выходных параметров.

Методы оптимизации РЭА.