Подготовка данных для ввода в компьютер для моделирования радиоэлектронных средств

Подготовка данных для ввода в компьютер.

1.Если в схеме содержаться многополюсники, то есть элементы не являющиеся R,L,C,I,E, то они должны быть представлены эквивалентными схемами (моделями)содержащими только  R,L,C,I,E.

2.В полученной эквивалентной схеме устройство ветви и узлы. Узел-точка, соединяющая две и более ветви. Ветвь содержит один элемент. 

3.Выбирается произвольным образом положительное направление тока в ветвях и полярность напряжения.

4.В произвольном порядке производим нумерацию узлом.

5.Производим нумерацию ветвей в следующем порядке:

1) Управляемые источники напряжения E_у.

2) Независимые источники напряжения E.

3) Ёмкостные элементы C.

4) Резисторы R.

5) Индуктивность L.

6) Независимые источники тока I.

7) Управляемые источники тока I_у.

6.Производим масштабирование параметров элементов,

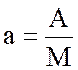      ,где М - масштабный коэффициент,

                           А - параметр элемента.

При получении данных от компьютера после моделирования, результаты необходимо умножить на масштабный коэффициент Α=a∙Μ → пользователь.

Введение в компьютер данные должны быть близки к 1.,с тем, чтобы компьютер не оперировал со слишком малыми и слишком большими величинами. Для получения масштабный коэффициента необходимо вычислить среднее геометрическое и если число дробное, то округлить его.

Масштабные коэффициенты связаны между собой:

 - закон Ома.

 

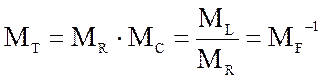
Таким образом, из семи масштабных коэффициентов независимыми могут быть выбраны лишь три. Остальные вычисляются исходя из этих независимых. В компьютер вводят  данные для каждой ветви:  1. номер ветви.

                          2. номер начального узла.

                          3. номер конечного узла.

                          4.тип ветви (R, L, C, I, E).

                          5. номинал.

 Лабораторные работы: 1. взять свой номер варианта и списать схему со стенда.

                                         2. подготовить данные к вводу в компьютер.

                                         3. найти масштабные коэффициенты, составить структурную матрицу.

ММС-состоит из двух   уравнений - компонентные и топологические уравнения.

Компонентные уравнения:

 

           

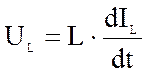
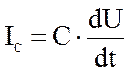Топологические уравнения – это способ соединения ветвей между собой. Топологические уравнения связаны  лишь с топологией схемы и не отражают типы ветвей и их параметры (законы Кирхгофа). Топологию схемы описывают с помощью графа. При построении графа, каждый узел анализируемого устройства представляется узлом в графе,  каждый ветвь устройства ветвью в графе соединяющая узлы графа и имеющая тоже направление.

Схема:

 

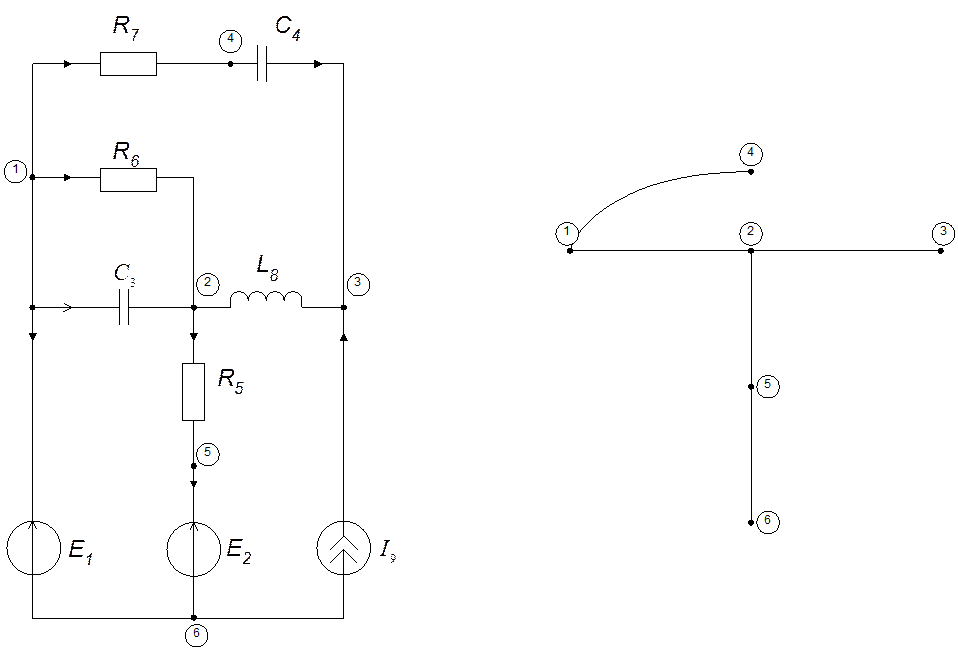
1)   нумеруем элементы,

2)   нумеруем узлы,

3)   задаём направление токов в ветвях.

Дерево графа (схемы) - это совокупность ветвей ,которая обеспечивает связь между всеми узлами графа, но не образует при этом замкнутых контуров.

Совокупность ветвей, не вошедших в дерево называется дополнением дерева. Ветви входящие

в дерево называется ребрами, а ветви дополнительного дерево называется хорды. Если узлов в схеме , ветвей , то  рёбер,  хорд.

Структурная матрица.

Запишем систему уравнений для шести узлов по закону Кирхгофа (со знаком плюс берём вытекающие).

1)

2)    

3)                        

4)  

5)  

6)  

Запишем эту систему в виде матрицы:

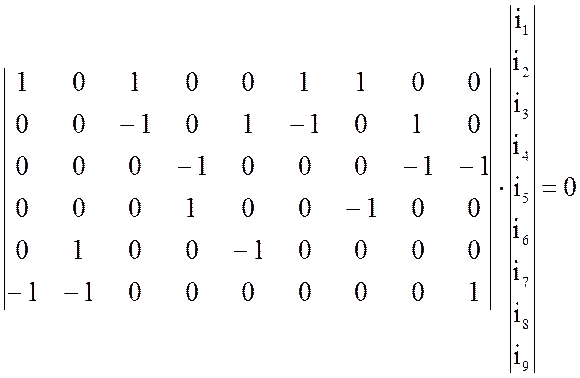
Одну строку можно вычеркнуть, так как она является избыточной (в каждом столбце) Таким образом, для построения структурной матрицы можно воспользоваться алгоритмом:

- элемент структурной матрицы ,если данная не присоединена к  данному узлу

-,если данная ветвь начинается в этом узле

-, если данная ветвь заканчивается в этом узле. В полученной матрице, одна из строк, чаще всего последняя (соответствует заземленному узлу) вычеркивается в силу избыточности.

Оставшаяся часть с одной вычеркнутой строкой называется структурной матрицей.

Структурной матрица не несёт полную информацию о топологии схемы. Эта матрица имеет размер ,где - количество узлов, а  - количество ветвей.

Топологические уравнения матрицы главных сечений.

Сечение схемы – это линия, условно разделяющая её на две части.

Главное сечение – это сечение проходящее только через одно ребро.

Мы будем пользоваться замкнутыми сечениями. Применим разные знаки токам, втекающим и вытекающим из области охваченной сечением. Тогда  закон Кирхгофа для токов, относительно сечений может быть сформулирован в виде: алгебраическая сумма токов относительно сечений равна нулю.

Главное дерево – это дерево, ветви в которое включены в порядке нумерации.

1.Сформируем главное дерево.

2. Построим главные сечения (5 рёбер соответственно 5 главных сеченй).

Запишем уравнения Кирхгофа для главных сечений:

                                                                            

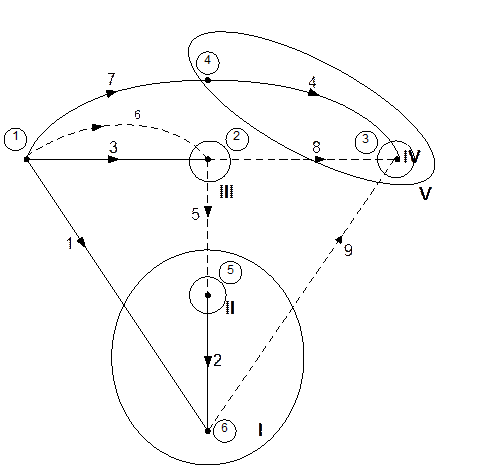
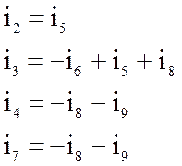                  (3)

Запишем в матричном виде:                                                  

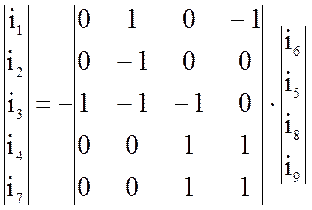 ,   (4)

где

- вектор токов хорд.            - вектор токов рёбер.

Запишем в общем виде:                                                                (5)                                                                                                                       

Это выражение показывает зависимость токов рёбер от токов хорд.

(5)- топологическое уравнение по законам Кирхгофа для токов произвольной схемы.

Рассмотрим структуру матрицы главных сечений.

Особенности матрицы главных сечений.

1. Взятые с обратным знаком элементы строки, представляют собой коэффициенты, линейно связывающие ток, соответствующего этой строке ребра, с токами хорд, в столбцах   которых расположены элементы.

2. Ненулевые элементы в столбце хорды показывают, с какими рёбрами  данная хорда образует замкнутый контур. При этом элементы представляют собой коэффициенты, с помощью которых напряжение хорд линейно выражается через напряжение рёбер.

Используя второе свойство, запишем систему уравнений,

 

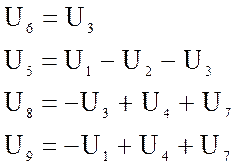
Запишем полную систему по закону Кирхгофа для напряжений в матричном виде:

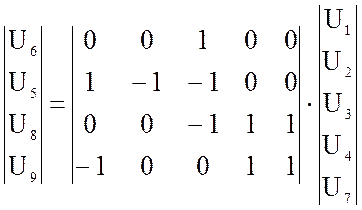                                               (6)      

                                                                                       (7)

Общий вид матрицы главных сечений без особенностей.

Элементы матрицы главных сечений можно разбить на подгруппы (подматрицы) , сгруппировав их по типам элементов, к которым они относятся. Тогда общий вид матрицы главных сечений для схемы без особенностей:

                                  

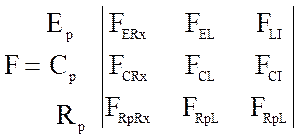                                                           (8)

Сформулированные выше правила построения топологических уравнений можно распространить их на случай, когда  матрицы главных сечений  в виде (8) то есть исходя из выражения  (7)

запишем  напряжение .

            

            

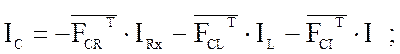
В электрических схемах  могут существовать многополюсники, то есть устройства имеющие n-выводов. Матрица полюсных проводимостей имеет размерность

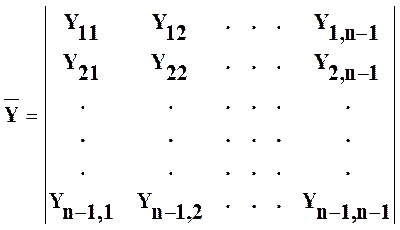
Для нахождения параметров матрицы :1.Все выводы многополюсники, кроме одного заземляют.

К оставшемуся j-выводу многополюсника подключают источник напряжения. В этом случае в матрице  полюсных проводимостей остается лишь j-столбец, а в векторе источников напряжений только

U_j .  Система уравнений М.М имеет вид , где .

2.Измеряют токи во всех  ветвях и элементах столбца, находим по формуле: .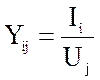

3.Далее измерения произведём при подключении источника напряжения к другому полюсу и так до заполнения всей матрицы .

4. Вектор токов находится заземлением всех полюсов многополюсника. Если в векторе тока есть ненулевые элементы, то в нём содержатся независимые источники E и I.

        Для описания многополюсников с использованием МУП наиболее удобно использование -параметров. Тогда эти  матрицы объединятся простым суммированием элементов.  

При составлении по методу узловых потенциалов математической модели

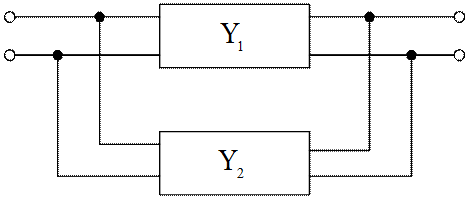схемы, содержащей многополюсники, элементы матрицы полюсных проводимостей многополюсника помещаются в соответствующие позиции, алгебраически суммируясь с содержимым этих позиций.

Элементы вектора полюсных токов также алгебраически сумми-