руются с соответствующими элементами вектора токов
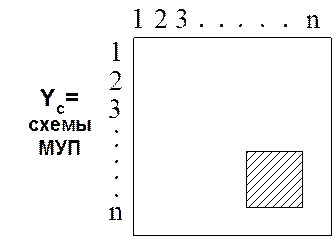
Пример схемы. (см. 3).
 |
|||
 |
|||
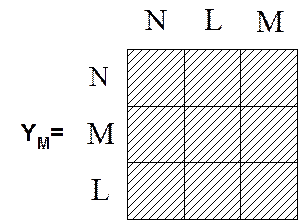
YM-матрица многополюсника.
Правило формирования матрицы узловых проводимостей и вектора источников тока.
Правило формирования матрицы узловых проводимостей:
1. Диагональные элементы 
матрицы узловых
проводимостей положительны и равны сумме проводимостей, подключенных к j –узлу.
2. Не диагональные элементы 
- отрицательны и равны сумме
проводимостей, включенных между j- иk- узлам.
Вектора источников тока.
1. Элементы jj – вектора токов равен сумме токов независимых источников, втекающих в j- узел.
2. Независимые источники напряжения должны быть преобразованы в источники тока с помощью преобразования Нортока.
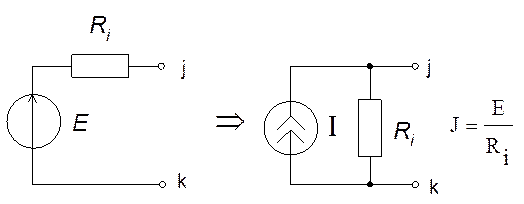
Все источники ЭДС необходимо преобразовать в источники тока. В случае применения в схеме неудобных элементов (направления идеальных источников напряжений), которые не позволяют перейти к источникам тока необходимо ввести активное внутреннее сопротивление (исходя из анализируемой схемы и параметров элементов).
Топологический метод составления уравнений по методу узловых потенциалов.
Для того чтобы разрабатывать математическую модель схемы для ЭВМ, необходимо рассматривать алгоритмы, которые легко формируются.
1. Все источники напряжения преобразовать в источники тока.
В любой ветви ток равен: 
.
Для цепи в целом : 
,где 
-
диагональная матрица, где по диагонали расположены проводимости ветвей.
Рассмотрим схему:
 |
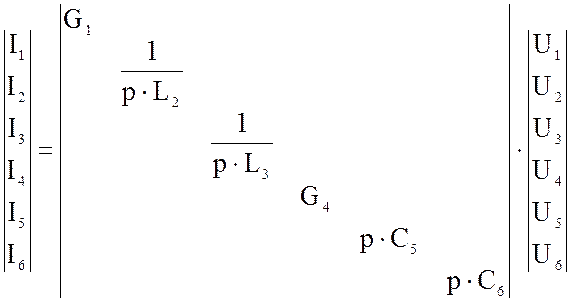
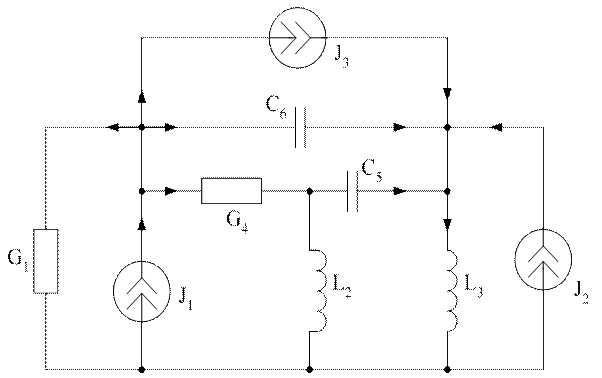Для схемы формируется структурная матрица (матрица
инцеденций), причем источники тока занимают в ней
последние столбцы и нумеруются отдельно. Структур-
ная матрица разбивается на подматрицы
,
где 
- подматрица источников тока.
Матрица проводимостей 
,где
-подматрица из структурной,
- вектор источника тока в ветвях.
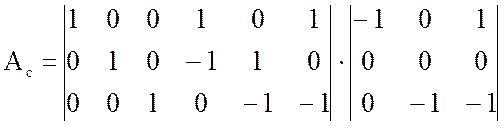
После вычисления получим матрицу узловых проводимостей.
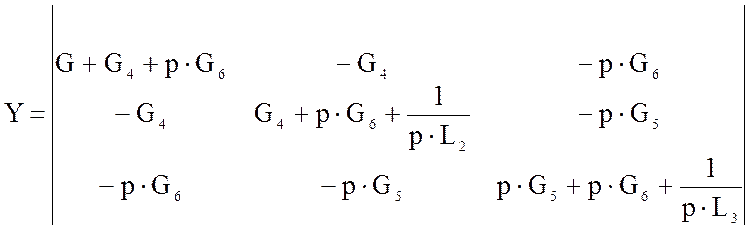
Вектор источников тока:
.
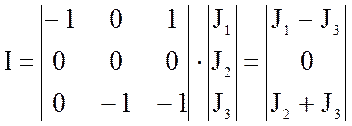Пример:
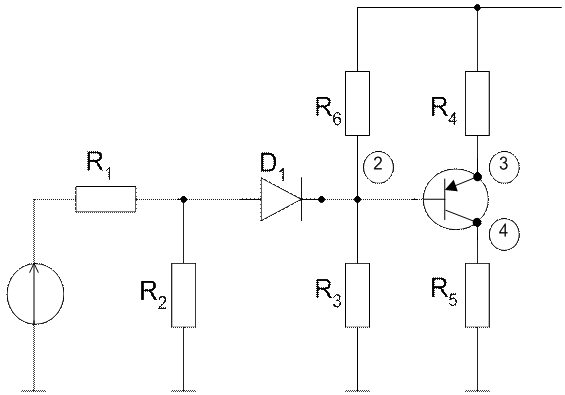
Имеем два многополюсника – диод и транзистор.
Матрица полюсных проводимостей:
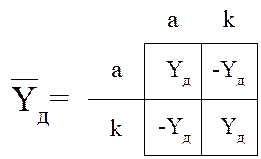
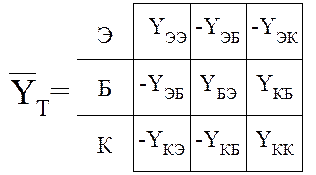
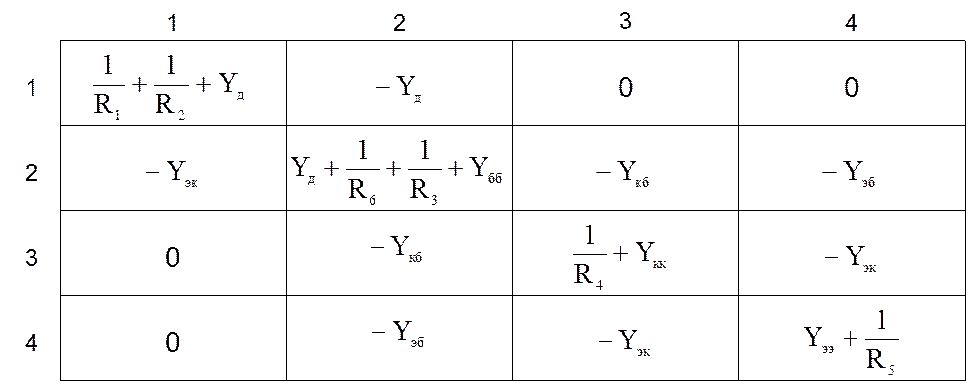
В связи с этим удобно пользоваться библиотекой стандартных элементов.
Зависимые источники (управляемые).
Наиболее часто используется источник тока управляемый напряжением:
 |
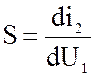-крутизна
источника.
Таблица для этого источника имеет вид:
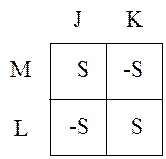
M, L- узел подключения управляемой ветви,
J, K- узлы подключения управляющей ветви,
причем L и J начальные узлы, а M и K конечные узлы.
На пересечении начальных и конечных узлов +S, если нет –S.
В данном случае имеются в виду идеальные источники.
Реальные источники обладают входной и выходной проводимостью.
С учётом этого таблица имеет вид:
 |
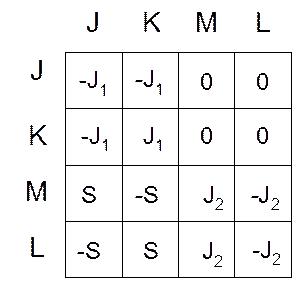
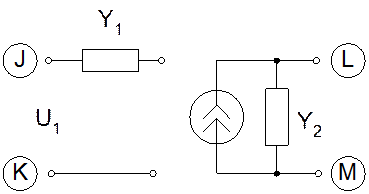Для примера рассмотрим низко частотную модель транзистора (модель Логона).
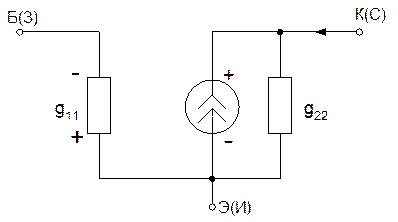Полярность дана для
транзистора обратной проводимости.
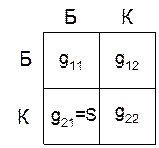
Для схемы с общим эммитером (
).
Динамический анализ цепей.
Динамический анализ цепей – это анализ переходных процессов в схеме при некоторых воздействиях.
Отклик цепи описывается системой дифференциальных уравнений n-порядка.
;
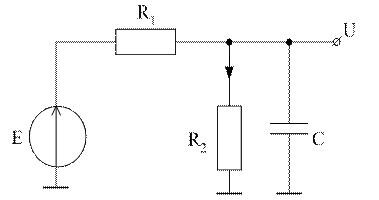
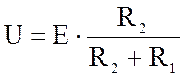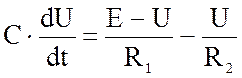
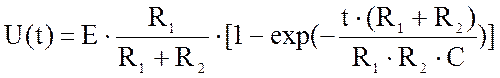(1)
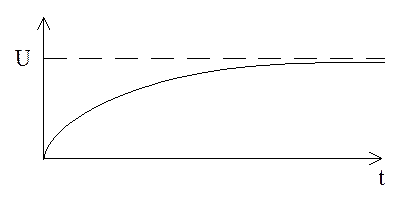Из уравнения (1) можно найти U(t) в точке t.
Уравнение (1) называется аналитическим решением.
Для реальных цепей выражение найти почти невозможно так
как: 1.схема
описывается, как правило, системой уравнений.
2. напряжение, как правило, имеют сложную форму воздейст-
вия.
3.зависимости напряжений от токов, как правило, нелинейны.
По этим причинам вместо аналитических выражений применяются численные методы.
Временные характеристики.
1(t)=h(t)-переходная характеристика.
d(t)=g(t)-импульсная характеристика.
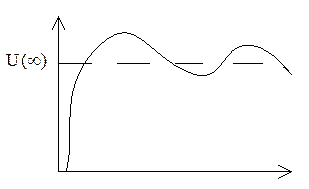
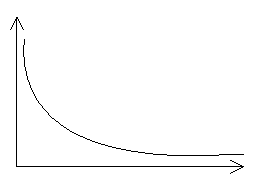
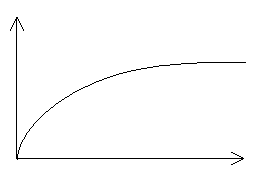срезает
высокие частоты передает высокие частоты
Явная форма математической модели схемы.
Существует две основных формы математической модели схемы явная и неявная.
Алгоритм формирования явнойматематической модели схемы.
1. Для схемы составляется главное дерево.
2. Составляется система уравнений для контуров, образованных индуктивными хордами и сечений образованных емкостными ветвями.
UL=f1(U),
iC=f2(i). (131)
3. iC и UL заменяются производными :Остальные переменные в системе выражаются через Uс(t) и iL(t) c помощью компонентных уравнений и законов Кирхгофа.
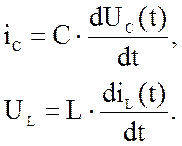
В результате получаем систему уравнений вида:
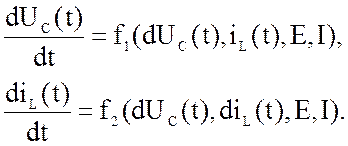(132)
Это система обыкновенных дифференциальных уравнений.
Таким образом, метод переходных состояний позволяет сформировать систему уравнений математической модели схемы в явном виде пригодную для математического анализа цепей.
Динамический анализ заключается в периодическом решении уравнений (132).
1. Добавив в (132) уравнение
токов резисторов: 
.
Производится статический расчет нахождения
начальных условий, 
и 
.
Подставляют эти условия в уравнения токов резисторов. Зачастую начальные
условия равны нулю.
2. Подставив эти данные в уравнение состояний, дав приращение для времени ∆t, решают систему уравнений каким- либо численным методом (132) то есть, находим UC(t+∆t) и iL(t+∆t).
3. Подставив найденные значения
вектора X(t1) в
уравнения токов резисторов, находим
значения вектора токов резисторов 
.
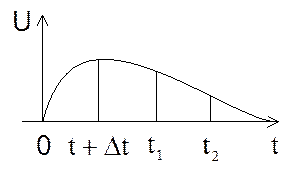
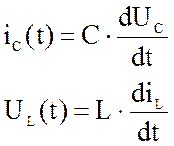
4. Со значениями X(t1) и переходим к пункту 2.
Пример реализации алгоритма.
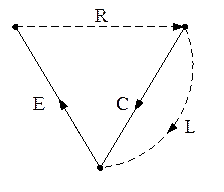
1) Строим
дерево (главное)
2) UL = UC
iC = iR-iL
Формирование математической модели схемы методом узловых потенциалов.
,где
- операторная проводимость.
,а
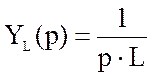,где 
-
ном. частота.
Закон Кирхгофа: сумма токов, вытекающих из узла через пассивные компоненты, равна сумме токов, вытекающих через независимые источники.
Схема:
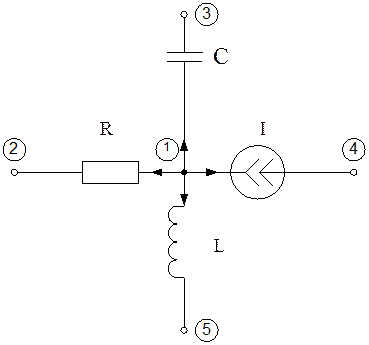
Представим токи в ветвях через их проводимости и узловые потенциалы, измеренные относительно нулевого узла.
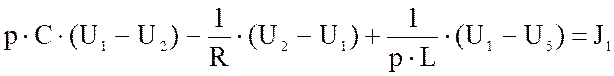
раскрываем скобки и преобразуем:
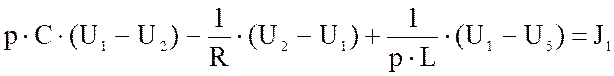
раскрываем скобки и преобразуем:
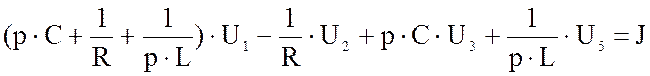
Получим уравнение по методу узловых потенциалов.
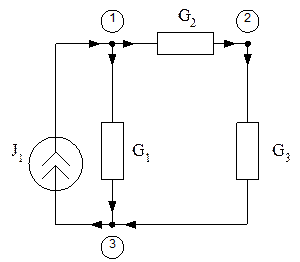Пример
1)
2) 
3) 
Разрешим эти уравнения относительно потенциалов (U).
1)
2)
3) 
Математическая модель схемы сформированная по методу узловых потенциалов.
В матричной форме запишем уравнения:
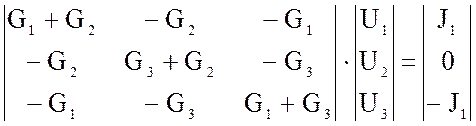
Сокращенная запись: 
,где 
-
матрица узловых проводимостей размером 
,а
- это количество узлов в
схеме,
- вектор узловых потенциалов,
- вектор источников тока.
Статический анализ схемы.
Находим все узловые напряжения и токи в ветвях, в том числе при синусоидальных воздействиях. -
Система уравнений для всех узлов
и опорного () имеет
ряд свойств:
1) Алгебраическая сумма
элементов неопределённой матрицы узловых проводимостей по
строкам
и столбцам вектора источников токов равны нулю.
2) Электрическая цепь с n- узлами может быть описана системой уравнений n- порядка. Однако в неопределённой системе одно уравнение линейно зависимо и может быть вычеркнуто. После вычеркивания переходим к определённой системе уравнений. Вычеркивается то уравнение, которое соответствует заземлённому или общему узлу. Если не определён общий узел общий узел, то общим объявляется тот узел, к которому подключено большее количество источников напряжения.
Для примера:
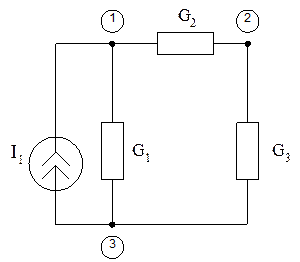
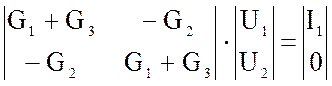- общий 
;
- общий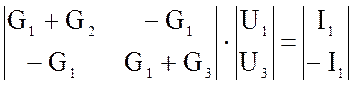 
;
Эквивалентная схема транзистора.
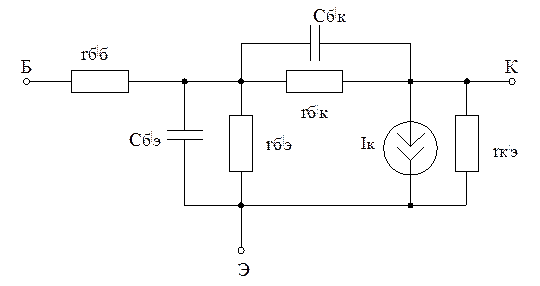
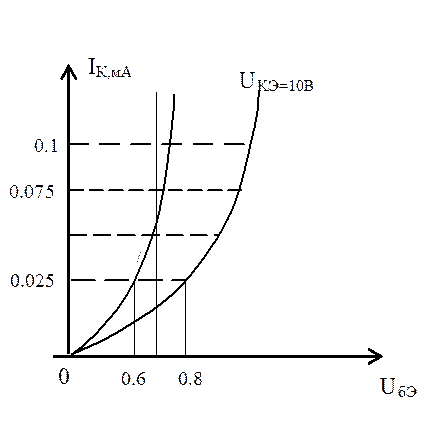
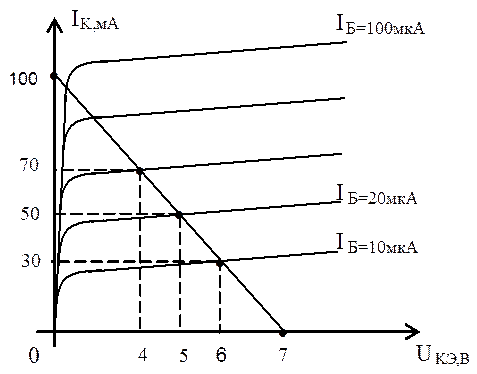
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.