Дискретизированные сигналы. Модулированные радиосигналы (3, 4 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева)

ГЛАВА  3 ДИСКРЕТИЗИРОВАННЫЕ СИГНАЛЫ

3.1. Дискретизированные сигналы и их математические модели

Известно, что сигнал — это физический процесс, несущий в себе некоторую информацию. Существуют, например, дискрет­ные импульсные и непрерывные сигналы s(t). Дискретные (им­пульсные) сигналы s(t) представляют собой последовательность одного или нескольких видеоимпульсов, которые могут перено­сить информацию в параметрах, характеризующих их: амплитуда, длительность, период следования. Разновидностью импульсных сигналов являются цифровые сигналы. Эти сигналы в определен­ных случаях можно представить кодовой группой импульсов, со­стоящей из множества импульсов, число, форма и значения па­раметров которых известны.

Дискретизированные сигналы ~ это сигналы, которые получе­ны путем дискретизации по определенным правилам непрерыв­ных сигналов. При этом Дискретизированные сигналы несут в себе информацию, присущую исходным непрерывным сигналам, в соответствии с которыми они получены. Представление дискретизированных сигналов в виде кодовых групп импульсов расши­ряет возможности по созданию радиотехнических устройств с ха­рактеристиками, которые могут быть существенно выше, чем у устройств, в которых обрабатываются непрерывные сигналы.

Дискретизированные сигналы представляют собой последова­тельность отсчетов (выборок) непрерывного сигнала s(t) взятых в определенные моменты времени nΔt, где п = 0, 1, 2, ... — целое число, Δt — шаг дискретизации сигнала s(t). На рис. 3.1 показаны замкнутая электрическая цепь и сигнал на ее выходе, электричес­кая цепь с ключом и дискретизированный сигнал на ее выходе.

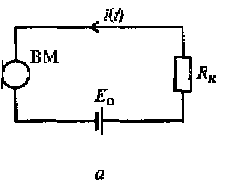
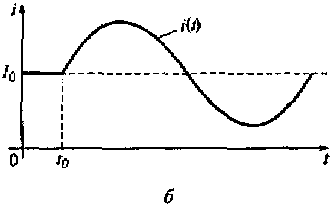
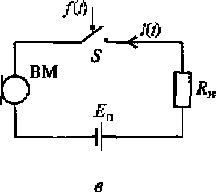
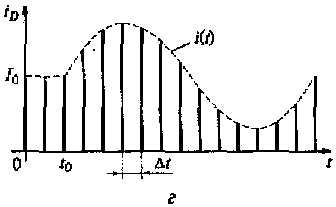
Рис. 3.1. Замкнутая электрическая цепь (и) и сигнал на ее выходе (£), электрическая цепь с ключом (в) и дискретизованный сигнал на ее выходе (г)

Допустим, имеется линия связи, на входе которой включен мик­рофон ВМ, а на выходе согтротишшние нагрузки R_H (см. рис. 3.1,а). При отсутствии акустического воздействия на микрофон наличие в цепи источника постоянного напряжения Е_п приводит к проте­канию в цепи постоянного тока I₀ (см, рис. 3.1,б),

При воздействии в момент t₀ звукового давления на мембрану микрофона физические процессы, происходящие в микрофоне, приведут к протеканию в цепи переменного тока i(t) (см. рис. 3.1, б). Этот ток является непрерывным сигналом. В каждый момент вре­мени он может быть измерен, а его форму можно проследить на экране осциллографа.

Введем в рассматриваемую цепь электронный ключ S (см. рис. 3.1,в), управляемый последовательностью бесконечно корот­ких импульсов f(t), следующих с интервалом времени Δt. В этом случае при замыкании ключа S в момент времени t= t₀ в цепи появляется ток, соответствующий величине аналогового сигнала в момент  t= t₀ (см. рис. 3.1,в). Соответственно при замыкании ключа в моменты времени nΔt, где n = 1, 2, 3, ..., в цепи будут появляться импульсы тока, амплитуды которых будут соответствовать ампли­тудам тока непрерывного сигнала в те же моменты времени. Последовательность импульсов тока i_D(nΔt) в цепи будет представ­лять собой дискретизированный сигнал (см. рис. 3.1,г), полученный путем дискретизации непрерывного сигнала. На рис. 3.2 представ­лена структурная схема устройства формирования дискретизиро­ванного сигнала.

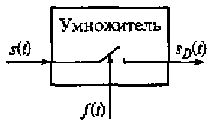
Рис. 3.2. Структурная схема устройства форми­рования дискретизированного сигнала

Последовательность бесконечно коротких импульсов f(t), уп­равляющих ключом S (см. рис. 3.1, в), можно описать суммой дель­та-функций, отстоящих друг от друга на величину Δt. В этом случае

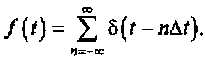(3.1)

С учетом (3.1) дискретизированный сигнал описывается про­изведением аналогового сигнала s(t) и функции управления f(t) (см. рис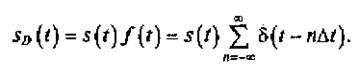. 3.2):

(3.2)

Поскольку импульсы в последовательности  f(t) появляются в конкретные моменты времени t_n = nΔt, то в эти же моменты сле­дует рассматривать и сигнал s(t). Тогда дискретизированный сиг­нал представляется в следующем виде (см. рис. 3.1, г):

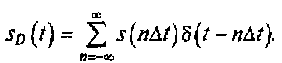
Данное выражение представляет модель дискретизированного сигнала. В нем величина s(nΔt) определяет значение непрерывно­го сигнала в момент времени nΔt, а дельта -функция δ(t – nΔt) обеспечивает выборку (фильтрацию) значений непрерывного сиг­нала в момент времени nΔt. На рис. 3.3 показаны непрерывный сигнал, последовательность коротких импульсов и дискретизиро­ванный импульс.

К решению практических задач ближе модель дискретизиро­ванного сигнала, в которой дельта-функция заменяется на описа­ние тактового прямоугольного импульса f_T(t) заданной амплиту­ды А и длительности τ_и (см. рис. 3.3, б):

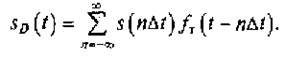
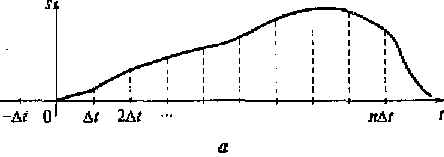
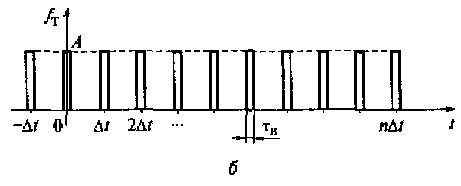
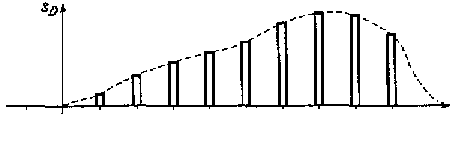
Рис. 3.3. Непрерывный сигнал (а), последовательность коротких импуль­сов (б) и дискретизированный сигнал (в)

В этом случае перемножение непрерывного сигнала s(t) (см. рис, 3.3,а) и прямоугольного импульса f_т(t) (см. рис. 3.3, б) в момент времени nΔt приведет к тому, что на выходе умножителя (см, рис. 3.2) появится импульс, длительность которого равна длительности прямоугольного импульса, а амплитуда - значению непрерывного сигнала в момент nΔt (рис. 3.3, в). Соответственно, умножение последовательности прямоугольных импульсов на непрерывный сигнал приводит к появлению на выходе умножителя последовательности дискретизированных сигналов (импульсов), несущих в себе всю информацию о непрерывном сигнале.

3.2. Ряд Котельникова

Для анализа сигналов широкое применение находит теорема Котельникова, которая формулируется следующим образом.

Если непрерывный сигнал s(t) имеет наивысшую круговую частоту спектральных составляющих ω_т = 2πf_m, то этот сигнал полностью определяется последовательностью значений своих выборок, взятых в моменты времени, отстоящие друг от друга не более чем на Δt= 1/2f_m.

Таким образом, согласно теореме Котельникова, сигнал со спек­тром, ограниченным частотой f_m = ω_т /2π, можно описать рядом

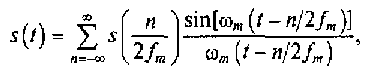(3.3)

где s(n/2 f_m) = s(nΔt) — выборки сигнала s(t) в моменты времени nΔt;

Δt= 1/2f_m — шаг дискретизации при выборке значений сигна­ла s(t).

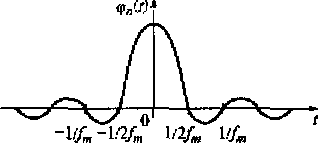
Рис. 3.4. Базисная функция рада Котельникова

Базисная функция ряда Котельникова (рис. 3.4) 

φ_n (t) = (sin[ω_m(t - п/2 f_m)])/ (ω_m(t - п/2 f_m)) = (sin[ω_m(t - пΔt)])/ (ω_m(t - пΔt))  в выражении (3.3) обладает следующими свойствами:

в точке t = nΔtфункция φ_n (t)  = 1, а в точках t = kΔt, где k ≠ n, φ_n (t)  = 0;

спектральная плотность функции φ_n (t)  равномерна в полосе частот - ω_m ≤ ω ≤ ω_m и равна 1/2 f_m. Амплитудный спектр равен 1/√2 f_m , а  фазовый — ехр(-jnωΔt);

интервал ортогональности базисных функций φ_n (t)  равен бес­конечности, а взаимная энергия ∫ φ_n²(t)dt равна Δt.

Исследование свойств базисных функций φ_n (t)  ряда Котель­никова доказывает, что эти функции ортонормированные. Таким образом, можно заключить, что в основе как ряда Фурье (2.6), так и ряда Котельникова (3.3) лежат базисы ортонормированных функций. Выборки значений непрерывного сигнала s(t) в точках nΔt, присутствующие в ряде Котельникова, не что иное, как ко­эффициенты ряда Фурье с_n = s(nΔt).

Таким образом, в роли умножителя может выступать элект­ронный ключ (см. рис. 3.2), на один из входов которого подается Непрерывный сигнал s(t), временная диаграмма которого, а так­же временные диаграммы последовательности импульсов дискретизированного сигнала и слагаемых ряда Котельникова показаны на рис. 3.5, а на другой — последовательность коротких импульсов f_T(t), следующих с интервалом Δt = 1/2f_т(см. рис. 3.5, б). В каждый момент времени nΔt на выходе ключа можно получить выборки исходного сигнала s(nΔt) (см. рис. 3.5, в). Эта последовательность выборок и представляет собой дискретизированный сигнал.