Дискретизированные сигналы. Модулированные радиосигналы (3, 4 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 2

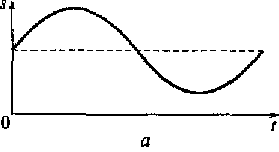
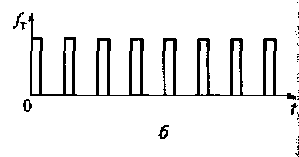
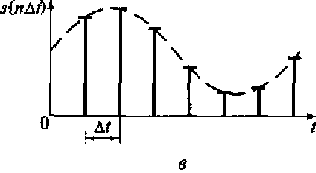
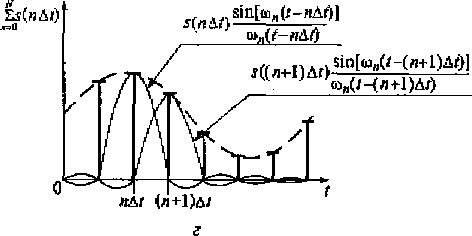
Рис. 3.5. Временные диаграммы непрерывного сигнала (а), последова­тельности тактовых импульсов (б), дискретизированного сигнала (в) слагаемых ряда Котельникова (г)

Тогда каждому моменту времени t_n=  nΔt в ряде Котельникова будет соответствовать слагаемое вида (см, рис, 3.5, г):

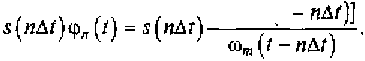
Сумма этих слагаемых позволяет аппроксимировать произвольный непрерывный сигнал s(t) с ограниченным спектром последовательностью выборок s(nΔt), если шаг дискретизации отвечает условию Δt = 1/2f_т. При этом достигается высокая точность аппроксимации. На практике точно выбрать временной интервал между выборками достаточно сложно. Поэтому при дискретизации непрерывных сигналов стремятся к тому, чтобы шаг дискретизации отвечал условию Δt ≤  1/2f_т .

Выбор величины Δtменьше 1/2f_тговорит о том, что в спектре сигнала имеется спектральная составляющая f_т1 с частотой более высокой, чем f_т. В этом случае рассматривается более широкий спектр сигнала и соответственно достигается его более точная аппроксимация дискретизированным сигналом. Если же  Δt будет больше 1/2f_тто это равносильно тому, что спектральные состав­ляющие исходного сигнала могут быть потеряны при аппрокси­мации, сокращая ширину спектра. Это может привести к потере информации при восстановлении непрерывного сигнала из дискретизированного.

Рассмотрим произвольный сигнал, для которого временной интервал существования равен Т_с. Пусть максимальная спектраль­ная составляющая этого сигнала имеет частоту f_m. Тогда полное число отчетов s(nΔt) сигнала

М = T_с/ Δt = 2T_cf_m.(3.4)

Число М в формуле (3.4) называется базой сигнала. Она харак­теризует сложность аппроксимации произвольного сигнала пос­ледовательностью дискретизированных выборок. Из (3.4) видно, что чем выше максимальная частота спектра сигнала f_т, тем меньше интервал дискретизации Δt и больше база сигнала М.

Ряд Котельникова в частотной области. Часто при анализе ра­диотехнических устройств возникает необходимость в представле­нии произвольного сигнала в виде суммы частотных выборок от спектральной плотности сигнала S(ω), а не временных выборок от сигнала s(t).

Пусть сигнал существует на временном интервале [-T_c/2, Т_с/2]. Заметим, что половина длительности сигнала аналогична полу­ширине спектра ω_т/2 в частотной области. Это позволяет произ­вести в формуле (3.3) замену функции времени tна функцию частоты ω, а шаг дискретизации Δt = 1/2f_mна интервал дискрети­зации Δω = 2π/Т_с. Тогда ряд Котельникова в частотной области можно представить следующим образом:

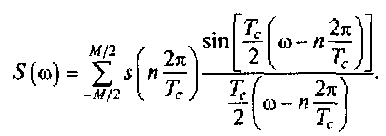(3.5)

В ряде Котельникова (3.3) шаг дискретизации не должен пре­вышать величины Δt = 1/2f_m, а в (3.5) частотный интервал дол­жен отвечать условию Δω = 2π/Т_с. В этом случае при ширине спектра 2ω_т (-ω_т ≤ ω ≤ ω_т) база сигнала будет определяться выражением М = 2ω_т/Δω = 2f_mT_c. Отсюда видно, что база сигнала не зависит от того, во временной (3.3) или частотной (3.5) областях сигнал аппроксимируется рядом Котельникова.

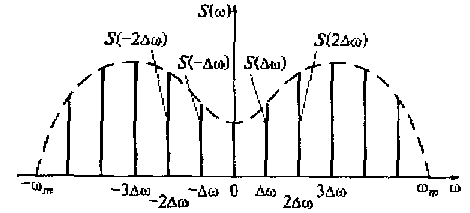
Рис. 3.6. Дискретизация спектра произвольного сигнала

В ряде Котельникова (3.5) выборки сигнала s[п(2π/Т_с] в общем случае являются комплексными величинами, т.е. описываются двумя параметрами: модулем и аргументом. Это говорит о том, что при аппроксимации определенного сигнала рядом Котельнико­ва в частотной области (3,5) требуется в 2 раза больше парамет­ров, чем для ряда Котельникова во временной области (3.3), когда в качестве переменной величины рассматривается только время. Это можно обойти, если учесть, что функции s[n(2π/T_c] и s[-n(2π/T_c] комплексно сопряженные, что видно из рис. 3.6, на котором пока­зана дискретизация спектра произвольного сигнала. Это позволяет число параметров, используемых в ряде (3.5), уменьшить в 2 раза.

Восстановление сигнала, дискретизнрованного рядом Котельни­кова. Процесс восстановления сигнала, дискретизированного ря­дом Котельникова, осуществляется с использованием фильтра нижних частот (ФНЧ) с комплексным коэффициентом передачи

K(jω).

Амплитудно-частотная характеристика (АЧХ) K(ω) этого филь­тра должна быть постоянна в диапазоне частот  -ω_т  ≤ ω ≤ ω_т  и рав­на 1√2f_т.

Фазочастотная характеристика (ФЧХ) φ(ω) этого фильтра дол­жна быть равна ехр(-jnωΔt). В результате этого в идеальном случае дискретизированный сигнал будет представлять собой дельта-фун­кцию. Для подтверждения того, что ФНЧ позволяет восстановить непрерывный сигнал по его дискретизированному аналогу, рас­смотрим реакцию фильтра на дельта-импульс.

На вход ФНЧ поступает дельта- импульс со спектральной плот­ностью

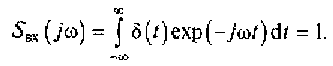
Спектральная плотность выходного сигнала составит

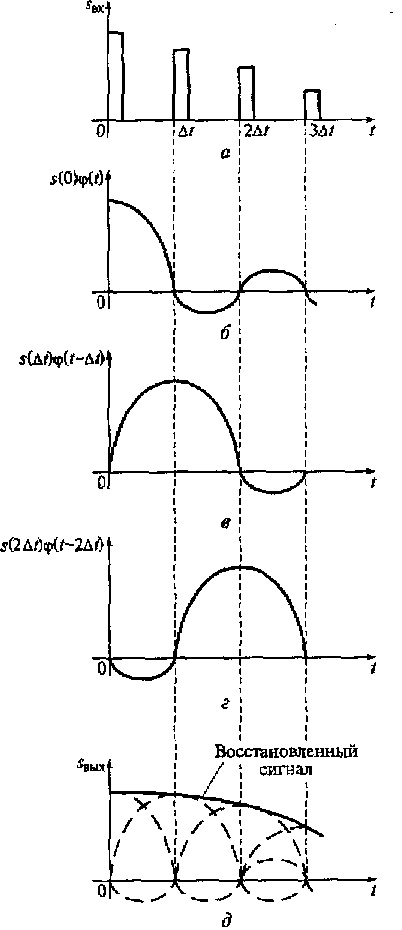
Рис. 3.7. Восстановление сигнала на выходе ФНЧ:

а — последовательность импульсов дискретизированного импульса; б, в, г — графики произведения базисной функции и выборки непрерывного сигнала со­ответственно при n= 0, 1, 2; д — восстановленный сигнал

        Используя обратное преобразование (2.18), найдем сигнал на выходе ФНЧ:

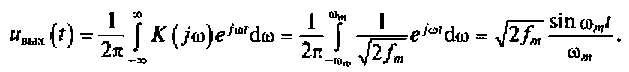
        Таким образом, сигнал на выходе ФНЧ при воздействии вход дельта-импульса, по форме повторяет базисную функцию (см. рис. 3,4) ряда Котельникова (3.3) в момент времени t_n =nΔt. На рис. 3.7 показан процесс восстановления сигнала на выходе ФНЧ.

        При поступлении на вход ФНЧ последовательности импуль­сов дискретизированного сигнала (см. рис. 3.7, а) на выходе ФНЧ через каждый интервал дискретизации Δt повторяется сигнал, представляющий собой произведение произвольных выборок сиг­нала s(nΔt) на базисные функции φ(t-nΔt).