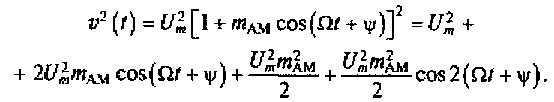Дискретизированные сигналы. Модулированные радиосигналы (3, 4 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 5

                                                       (4.5)

Известно, что средняя мощность сигнала, изменяющегося по гармоническому закону, равна нулю. Тогда  P_cp.ν = U_m²(1 + 0, 5 m_AM² ). Видно, что средняя мощность АМ-колебания зависит как от квад­рата амплитуды несущего колебания U_m², так и от квадрата коэф­фициента амплитудной модуляции  m_AM. При m_AM = 0 средняя мощ­ность АМ-колебания равна средней мощности несущего колеба­ния P₀= U_m².

При m_AM≠0 средняя мощность АМ-колебания в (1 + 0, 5 m_AM² ) раз выше средней мощности несущего колебания Р₀. При  m_AM = 1 достигается максимальная средняя мощность АМ-колебания Р_max = 1,5Р₀.

Из выражения (4.5) при условии, что m_AM =1 и cos(x) = 1, можно найти пиковую мощность АМ-колебания Р_пик =4Р₀.

4.3. Спектр АМ-колебаний при тональной модуляции

Рассмотрим спектр АМ-колебания, используя выражение (4.3). В этом выражении имеются две гармонические составляющие. Одна из них с частотой ω₀ характеризует несущее колебание u_н(t), име­ющее амплитуду U_mи начальную фазу φ₀ а другая с частотой Ω— управляющий сигнал u_у(t), имеющий амплитуду U_yи начальную фазу ψ. В данном случае управляющий сигнал u_y(t) является то­нальным, изменяющимся только в соответствии с одной частотой Ω. Как правило, в устройствах модуляции выполняется условие ω₀» Ω. С учетом этого на рис. 4.4 показаны амплитуды и началь­ные фазы несущего колебания и управляющего сигнала.

В целях анализа спектра АМ-колебания к выражению (4,3) при­меним ряд математических преобразований: во-первых, раскроем квадратные скобки; во-вторых, разложим произведение косину­сов по формуле cosαcosβ = 0,5[cos(α + β) + cos(α-β)]. В результате этого получим

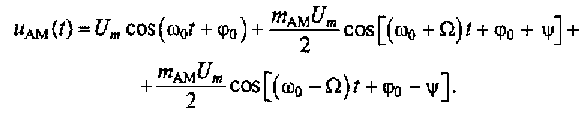                                                   (4.6)

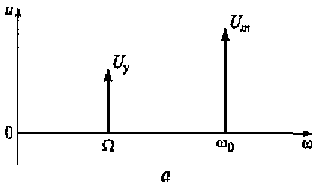
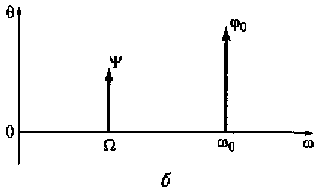
Рис. 4.4. Амплитуды (a) и началь­ные фазы (б) несущего колебания иуправляющего сигнала

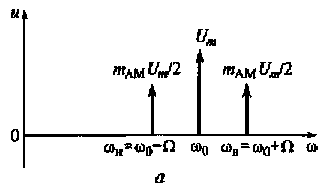
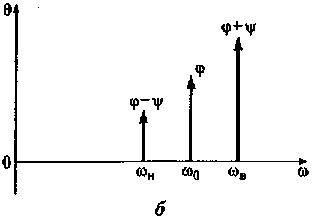
Рис. 4.5. Спектр амплитуд (а) и спектр фаз (6) АМ-колебания при тональной модуляции

Из выражения (4.6) видно, что AM-колебание при тональной модуляции представляет собой сумму трех спектральных состав­ляющих. На рис. 4.5 показаны спектры амплитуд и фаз АМ-колебания при тональной модуляции.

Одна из спектральных составляющих характеризует несущее коле­бание U_mcos(ω₀t+φ₀) с частотой ω₀, амплитудой U_m(см. рис. 4.5, а) и начальной фазой φ₀(см. рис. 4.5, б). Две другие спектральные со­ставляющие (m_AMU_m/2)cos[(ω₀-Ω)t+φ₀-ψ] и  (m_AMU_m/2)cos[(ω₀+Ω)t+φ₀+ψ]соответствуют нижней ω_н = ω₀ - Ω и ω_в = ω₀ + Ω верхней  частотам спектра АМ-колебания. Амплитуды этих спектральных составляющих равны между собой m_AMU_m/2 . Эти амплитуды даже  при m_AM= 1 не могут быть больше половины амплитудного значе­ния несущего колебания U_m/2. Фазы этих спектральных состав­ляющих соответственно равны  φ-ψ и  φ+ψ. Ширина спектра АМ-колебания, модулированного тональным сигналом, F= ω_в- ω_н = 2Ω.

Таким образом, ширина спектра АМ-колебания при тональной модуляции равна удвоенной частоте управляющего сигнала, а спектр симметричен относительно частоты  ω₀  несущего колебания.

4.4. Спектр АМ-колебаний при модуляции сложными сигналами

Рассмотрим спектр АМ-колебания, который получен при ис­пользовании управляющего сигнала u_у(t) = u_ycos(Ω₁t) + u_ycos(Ω₂t), содержащего две гармонические составляющие с равными ампли­тудами U_yи различными частотами Ω₁ и Ω₂ (Ω₁< Ω₂). В этом случае спектр AM-колебания может быть описан следующим образом:

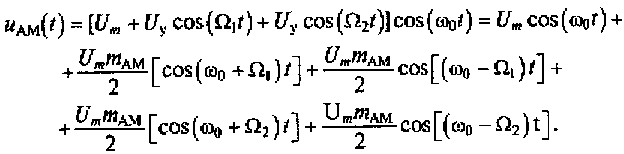                                              (4.7)

При наличии двух спектральных составляющих в управляющем сигнале u_y(t) АМ-колебание имеет пять спектральных составляю­щих (4.7). В спектре АМ-колебания при двух спектральных состав­ляющих управляющего сигнала (рис. 4.6) имеется составляющая несущего колебания с амплитудой U_mа также четыре спектраль­ные составляющие с амплитудами m_AMU_m/ 2, которые соответствуют частотам: ω₀-Ω₂, ω₀- Ω₁, ω₀+Ω₂ и ω₀+Ω₁  . Ширина спектра подоб­ного АМ-колебаниям определяется наивысшей частотой управля­ющего сигнала (Ω₂> Ω₁) и имеет вид ω₀+Ω₂-( ω₀-Ω₂)=2 Ω₂.

В общем случае амплитуды спектральных составляющих управ­ляющего сигнала u_y(t)  имеют разные амплитуды. Каждой спектральной составляющей АМ-колебания (4.7) соответствует свой коэффициент амплитудной модуляции m_Ami.

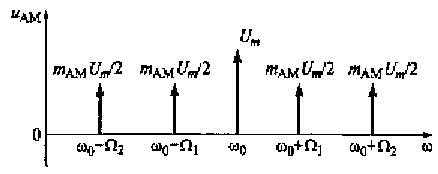
Рис. 4.6. Спектр АМ-колебания при двух спектральных составляющих управляющего сигнала

Амплитуды различ­ных спектральных составляющих не будут равны друг другу и определяются величиной m_АМiU_m/2, где i= 1, 2, 3 ... — номер спектральной составляющей управляющего сигнала.

В случае, когда управляющий сигнал u_y(t) имеет множество гармонических составляющих с частотами от Ω_min до Ω_max, шири­на спектра АМ-колебания будет определяться выражением 2Ω_max. На рис. 4.7 показан дискретный спектр АМ-колебания.

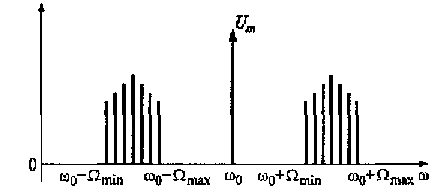
Рис. 4.7. Дискретный спектр АМ-колебания

Рассмотрим формирование спектра АМ-колебания, когда уп­равляющий сигнал имеет сложный вид. Например, в качестве уп­равляющего сигнала используется электрический сигнал от микрофона. В этом случае спектр АМ-колебания можно описать, используя выражение прямого преобразования Фурье (2.17):

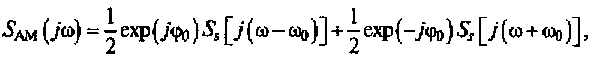(4.8)

где S_s [j(ω – ω₀ )]и S_s [j(ω + ω₀ )]  — спектральные плотности огибаю­щей АМ-колебания в интервалах частот ω – ω₀ и ω + ω₀.

Из выражения (4.8) видно, что спектральная плотность АМ-колебания разбивается на две части. Одна часть спектра концент­рируется в области отрицательной частоты ω = - ω₀, а другая — частоты ω = ω₀. На рис. 4.8 показана спектральная плотность АМ-сигнала.