Дискретизированные сигналы. Модулированные радиосигналы (3, 4 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 3

        На рис. 3.7,б,в,г представлены графики, характеризующие произведение базисной функции (см. рис. 3.4) и выборки непре­рывного сигнала соответственно при п = 0, 1, 2.

        Восстановленный сигнал (см. рис. 3.7,д) будет представлять собой сумму произведений выборок сигнала и базисных функций s(nΔt)φ(t-nΔt) при соответствующих п.

        При соблюдении условия по выбору шага дискретизации  Δt=1/2f_т можно говорить, что сигнал восстанавливается с высокой точностью.

3.3. Спектр дискретизированного сигнала

        Рассмотрим спектр дискретизированного сигнала, используя его модель (3.2) и считая, что спектральная плотность исходного сигнала равна S(jω). В этом случае дискретизированный сигнал можно представить в виде S_D = s(t)f_T(t).

         Периодическую последовательность управляющих импульсовf_T(t) можно рассматривать как периодическую последовательность прямоугольных импульсов длительностью τ_и и скважностью следования q=Т/ τ_и . Применив обобщенный ряд Фурье, находим спектральную плотность дискретизированного сигнала:

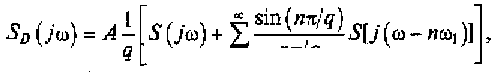
где ω₁ = 2π/Т — частота следования прямоугольных импульсов.

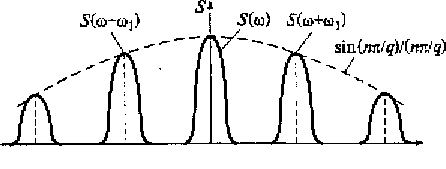
         Рассматривая это выражение, можно сделать следующие выво­ды, наглядно подтверждаемые спектром дискретизированного сигнала (рис. 3.8).

                                          -4π/Т     -2π/Т    -ω_т 0  ω_т   2π/Т   4π/Т ω  

Рис. 3.8, Спектр дискретизированного сигнала

1.  Спектр дискретизированного сигнала s_d(jω) представляется последовательностью спектров S(jω) исходного сигнала s(t) и спектров S[j(ω-nω₁)], сдвинутых по оси частот друг относитель­но друга на величину лей nω₁= 2π/Т  и убывающих по амплитуде в соответствии с функцией

sin(nπ/q) 

nπ/q

2.  Период T(Δt) следования управляющих импульсов f_T(t) на практике выбирают исходя из условия Т < ½ f_T . Это повышает степень воспроизведения сигналов, обеспечивает неперекрывае­мость отдельных спектров S[j(ω±nω₁)] и возможность их каче­ственного выделения с помощью фильтров.

3. При увеличении скважности qследования управляющих им­пульсов f_T(t), т.е. уменьшении τ_и, при сохранении периода Tследования импульсов постоянным, амплитуда боковых лепестков спектра уменьшается, сами лепестки сужаются, а спектр приоб­ретает строго периодическую структуру. В пределе при τ_и , стре­мящемся к нулю, а А к бесконечности, и постоянстве произведения  τ_иA управляющие импульсы и составляющие дискретизированного сигнала приобретают вид дельта-функций

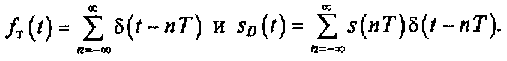
В этом случае спектр дискретизированного сигнала принимает вид

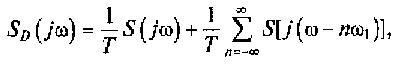
т.е. функция  sin(nπ/q)  стремитсяк единице при различных n, а

nπ/q

разные лепестки спектра имеют практически одинаковую ампли­туду.

ГЛАВА 4 МОДУЛИРОВАННЫЕ РАДИОСИГНАЛЫ

4.1. Общие определения

Радиосигналы можно разделить на два класса:

детерминированные сигналы, которые не несут в себе информации, но могут быть использованы для переноса информант поступающей от различных источников сообщений;

управляющие сигналы, которые изменяются по случайному закону и несут в себе информацию.

Как правило, управляющие сигналы в сравнении с сигналами—переносчиками сообщений являются относительно низкочастотными (звуковой сигнал, музыка, телеграфный код). Пере­дать подобные сигналы на большие расстояния в различных линиях связи (радиоканал, волоконно-оптическая или проводная линии связи) практически невозможно. Это связано, как с осо­бенностями распространения электромагнитных волн в линиях связи, так и с тем, что в одной линии приходится передавать сигналы, несущие различную информацию. Выполнить это в ком частотном диапазоне невозможно.

В целях преодоления этих ограничений в радиотехнических yустройствах используют операцию преобразования сигналов, называемую модуляцией.

Под модуляцией понимают изменение какого-либо параметра вполне определенного (детерминированного) сигнала в соответствии с изменениями управляющего сигнала, несущего сообщение. Детерминированный сигнал, параметры которого изменятся в ходе модуляции, называется модулируемым или несущим колебанием. Управляющий сигнал, в котором присутствует информация, называется модулирующим сигналом. Сигнал, полученный ходе модуляции, называется модулированным колебанием.

На рис. 4,1 показаны следующие виды несущих колебаний, их пользуемых при модуляции сигналов:

а) гармонические колебания (см. рис. 4.1, а), изменяющиеся по закону синуса u(t) = U_msin(ω₀t);

б) последовательность прямоугольных импульсов (см. рис. 4.1,6);

в)  постоянный ток (см. рис. 4.1, в);

г)  шумоподобные сигналы (см. рис. 4.1, г), представляющий собой последовательность единичных интервалов длительностью τ, которым поставлены в соответствие случайным образом расположенные простейшие по форме сигналы: прямоугольные импульсы, sin x, cos x и т.д.

В каждом из несущих колебаний имеются несколько параметров, изменяя которые можно получить модулированный сигнал.

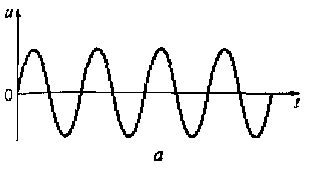
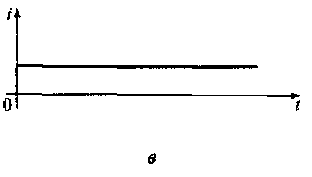
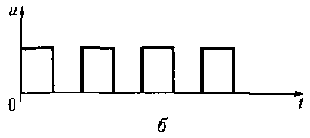
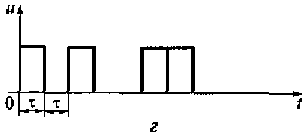
Рис. 4.1. Виды несущих колебаний:

a — гармоническое колебание;б — последовательность прямоугольных импуль­сов; в — постоянный ток; г — шумоподобный сигнал

Соответственно число возможных видов модуляции для данного несущего колебания ограничено. Так, при использовании в каче­стве несущего колебания сигнала, изменяющегося по закону ко­синуса (см. рис. 4.1, а), можно получить сигналы с амплитудной (AM), частотной (ЧМ) и фазовой (ФМ) модуляциями. В первом случае амплитуда U_mнесущего колебания модулируется в соответ­ствии с изменениями мгновенного значения модулирующего сиг­нала. Во втором случае модулируется частота, а в третьем — фаза в соответствии с изменениями мгновенного значения модулиру­ющего сигнала.