ЛАБОРАТОРНАЯ РАБОТА №4
ПРЕОБРАЗОВАНИЕ ЧАСТОТЫ
Цель работы: изучение основных закономерностей преобразования частоты. В работе снимается зависимость коэффициента преобразования от напряжения смещения, исследуются спектры сигналов на выходе преобразователя при большой и малой амплитудах гетеродина.
Приборы и оборудование: базовый блок и сменное устройство. В сменном устройстве находятся нелинейный элемент – транзистор, гетеродин, генерирующий колебания с частотой fг, фильтр промежуточной частоты, настроенный на частоту fп, фильтр нижних частот, органы коммутации и регулировки.
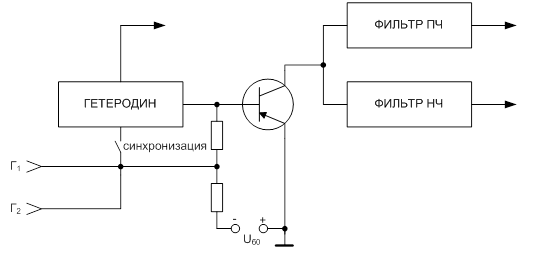
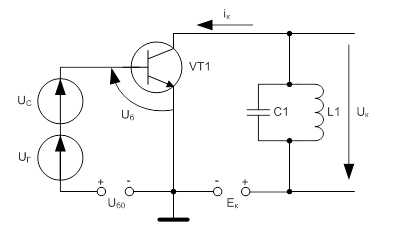
Рис. 1 – Структурная и принципиальная схемы преобразователя частоты
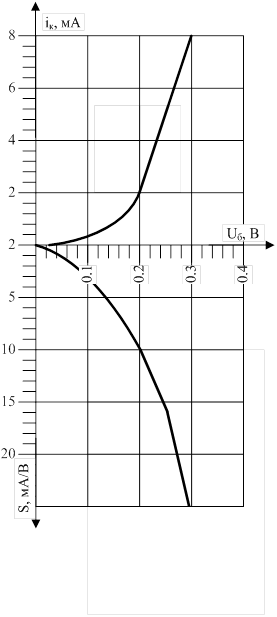
Параметры лабораторного макета:
Lк=750 мкГн
Cк=2200 пФ
fг=250±2 кГц
Uг=10 мВ (малая)
Uг=250 мВ (большая)
Rн=3 кОм
Максимальная амплитуда сигнала на выходе будет иметь место в тех случаях, когда промежуточная (выходная) частота будет равна частоте резонанса колебательного контура:
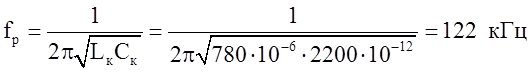
Таким образом, из условия для квадратичного преобразования:
|
![]()
Частоты сигнала, отвечающие условию резонанса на выходе транзистора:
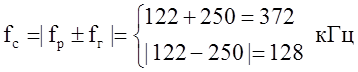
На большом сигнале условие для промежуточной частоты следующее:
![]()
Значит частота сигнала:
![]()
Так как крутизна преобразования равна половине амплитуды первой гармоники дифференциальной крутизны параметрического элемента:
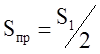
Напряжение на выходе преобразователя в режиме преобразования частоты будет описываться следующим образом:
![]()
![]()
Положим Uс=1 мВ, тогда зависимость Uвых(Uб0):
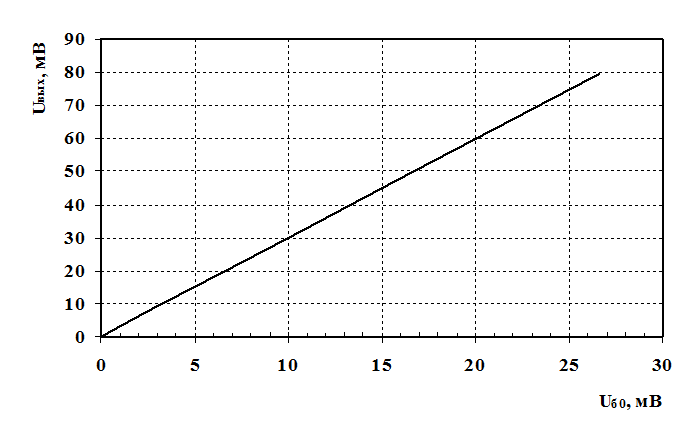
Рис. 3 – Зависимость напряжения на выходе преобразователя от напряжения смещения в режиме преобразования
ЛАБОРАТОРНАЯ РАБОТА
Снимаем зависимость напряжения на выходе преобразователя от напряжения смещения Uвых(Uб0) в режиме прямого прохождения при Uс=10 мВ, fс=fп и выключенном гетеродине:
|
Uб0, В |
Uвых, мВ |
|
0 |
2.0 |
|
0.40 |
3.0 |
|
0.50 |
3.5 |
|
0.58 |
4.0 |
|
0.68 |
4.5 |
|
0.76 |
5.0 |
|
0.92 |
6.0 |
|
0.95 |
8.0 |
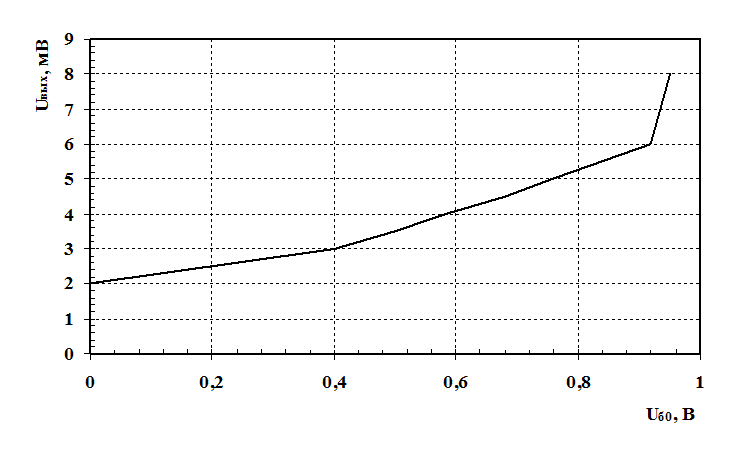
Рис. 4 – Зависимость напряжения на выходе преобразователя от напряжения смещения
Выбираем рабочую точку на середине линейного участка зависимости Uвых(Uб0): Uб0=0.65 В
Снимаем и строим зависимость напряжения на выходе преобразователя от частоты сигнала при Uс=10 мВ:
|
малая амплитуда |
большая амплитуда |
||
|
fс, кГц |
Uвых, мВ |
fс, кГц |
Uвых, мВ |
|
123 |
40 |
178 |
83 |
|
183 |
40 |
363 |
80 |
|
830 |
25 |
400 |
95 |

Рис. 5 – Частоты сигнала, дающие максимумы напряжения на выходе преобразователя
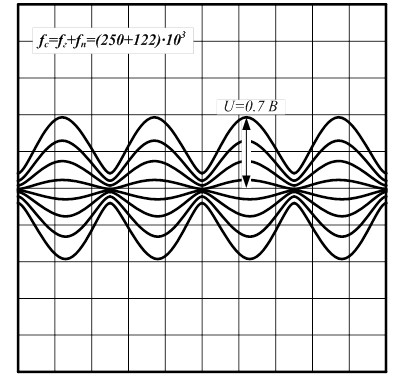
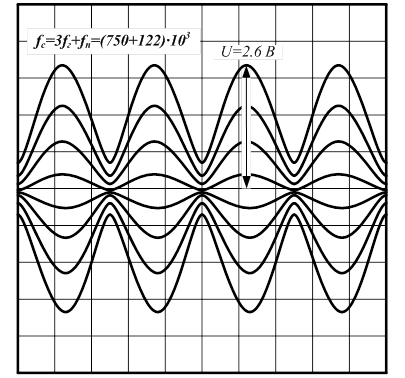
Фиксируем осциллограммы АМ-напряжения на выходе преобразователя при Uс=10 мВ, M=30 %, F=400 Гц, большой амплитуде гетеродина и смещении Uб0=0.5 В:
Снимаем зависимость Uвых(Uб0) при большой амплитуде гетеродина:
|
Uб0, В |
Uвых, В |
|
0 |
1.10 |
|
0.1 |
1.50 |
|
0.2 |
1.60 |
|
0.3 |
1.60 |
|
0.4 |
1.60 |
|
0.6 |
1.75 |
|
0.8 |
2.00 |
|
1.0 |
2.50 |
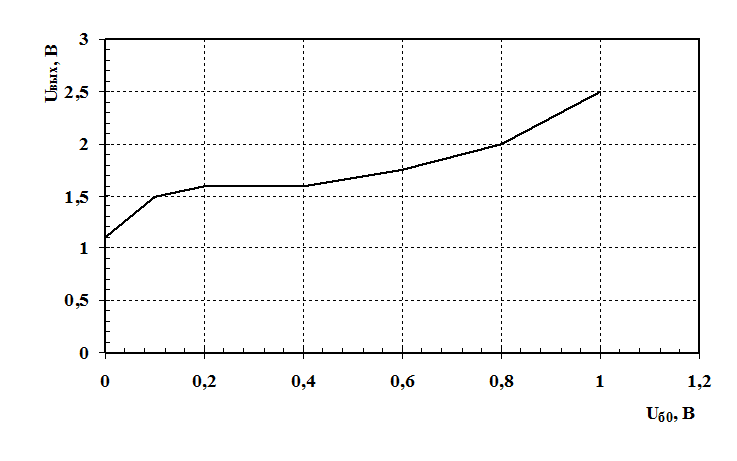
Рис. 6 – Зависимость выходного напряжения преобразователя от величины смещения при большой Uг
Рассчитываем зависимость коэффициента преобразования от смещения Кпр(Uб0), используя результаты, полученные выше:
|
Uб0, В |
Кпр |
|
0 |
110 |
|
0.1 |
150 |
|
0.2 |
160 |
|
0.3 |
160 |
|
0.4 |
160 |
|
0.6 |
175 |
|
0.8 |
200 |
|
1.0 |
250 |
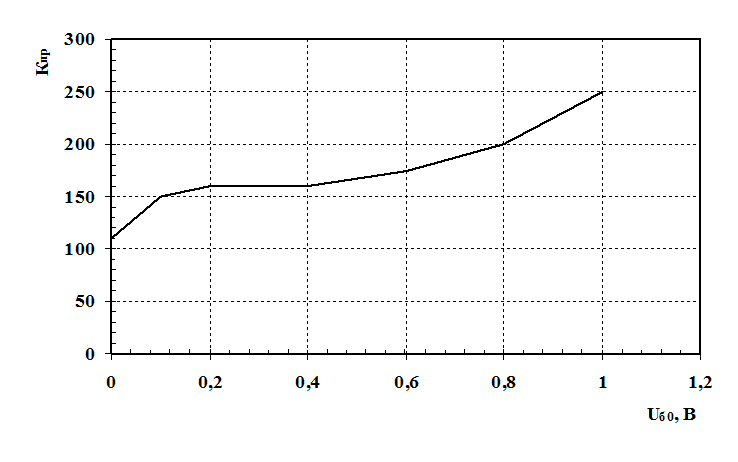
Рис. 7 – Зависимость коэффициента преобразования от величины смещения при большой Uг
Вывод: проделав данную работу, мы изучили основные физические принципы преобразования частоты несущей АМ-колебания; определили частоты сигнала, дающие максимальный коэффициент передачи преобразователя и зафиксировали эпюры преобразованного сигнала, который (как и следует из теории) не меняя формы огибающей, заполнялся частотой, отличной от входной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.