Построение математической модели колебания струны на основе теории распределенных сигналов

СОДЕРЖАНИЕ

Введение                                                                                                             3               

1 Моделирование на микроуровне                                                                  4

1.1 Выбор уравнения и его идентификация                                                    4   

1.2 Расчет статической характеристики                                                           5                                                                                

1.3 Расчет динамической характеристики                                                       8                                                                               

1.4 Моделирование струны в среде Elcut                                                        10                                                

2 Моделирование на макроуровне                                                                   12      

2.1 Исходные данные                                                                                         12                                                                                                                                                              

2.2 Графические формы математической модели гидросистем                     13                    

2.2.1 Динамическая схема                                                                       13                                       

2.2.2  Орграф                                                                                                      13

2.2.3 Матрица   инциденций                                                                             14

2.3 Узловой метод формирования математической модели

гидросистемы                                                                                                     16

2.4 Расчет статической модели гидросистемы                                                19                           

2.5 Анализ динамической модели гидросистемы                                           23

2.5.1 Выбор шага интегрирования                                                                   25

2.5.2 Решение систем дифференциальных уравнений методом Эйлера      26

Заключение                                                                                                         30

Список использованной литературы                                                               31

Приложение                                                                                                        32

ВВЕДЕНИЕ

Системой с распределенными параметрами (СРП) называется система, в которой практически все сигналы (в первую очередь – входной и выходной) являются функциями пространственных координат и времени. Таким образом, параметры СРП оказываются как бы распределены в пространстве, отсюда и название. Иногда СРП называются диффузными системами. Одним из примеров СРП могут служить т.н. «длинные линии», изучаемые в курсе электротехники, т.е. проводники, размеры которых сопоставимы с длиной волны, а электрические параметры (сопротивление, емкость и индуктивность) распределены по всей длине.

Математически СРП описываются дифференциальными уравнениями в частных производных, также для этого вводятся функции Грина, континуальная и интегральная передаточные функции.

Система с сосредоточенными параметрами (ССП) является частным случаем СРП и вводится для упрощения и решения задач на первом этапе. В большинстве случаев такого упрощения оказывается достаточно для получения адекватных результатов, но в ряде задач распределение параметров в пространстве оказывает существенное воздействие на результаты, в этом случае применяется аппарат теории СРП.

Целью курсовой работы является синтез интегральной передаточной функции для объектов управления с распределенными параметрами. В данной работе решается вопрос построения математической модели колебания струны на основе теории распределенных сигналов: по заданному дифференциальному уравнению объекта получить выражение для передаточной функции в распределенных параметрах, выражение для выходной величины, выражение для оценочной передаточной функции для наилучших условий управления. Построить оценочную ЛАЧХ, аппроксимировать ее и записать выражение передаточной функции через типовые звенья.

1 МОДЕЛИРОВАНИЕ НА МИКРОУРОВНЕ

1.1 Выбор уравнения и его идентификация

Есть среды, которые не могут быть описаны в сосредоточенных параметрах (электромагнитное поле, электростатическое поле, течение потока, гравитационное поле, температура и т.д.), поэтому они рассматриваются как системы с распределенными параметрами.

Конечной задачей решения уравнения СРП является нахождение выходной распределенной величины Q(x,t) в любой момент времени (t>0) в любой пространственной точке X.

Рассмотрим уравнение гиперболического типа, описывающее колебательные процессы [1]:

 ,

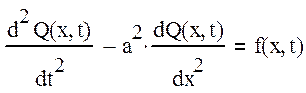где f(x,t) – входная координата по среде, зависящая от трехмерной координаты x и времени t,                  

 для которого формируются следующие  условия [1]:                      

- начальные условия:

               Q(x,0)=Q₀(x)

  ;

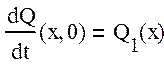- граничные условия:

- стандартизирующая функция, компенсируя влияние начальных и граничных условий для данной задачи, имеет вид [1]:

                   ;                                   

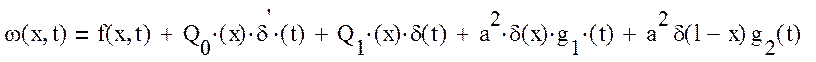- функция Грина, являющаяся решением краевой задачи при нулевых начальных и граничных условиях и входном воздействии в виде                   δ – функции, имеет вид [1]:

                                                       

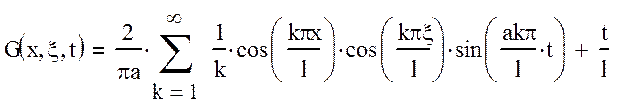
- континуальная передаточная функция, являющаяся преобразованием Лапласа функции Грина, является производной и всегда может определиться по функции Грина, имеет вид [1]:                                                                               

  

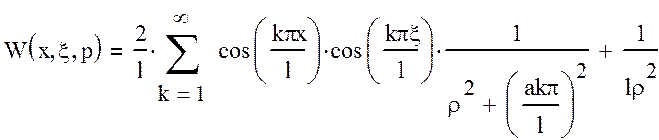
    Для решения частной задачи примем следующие условия:

- входное воздействие:

f(x,t) = 0;

- начальные условия, описывающие колебания струны  в начальный момент времени:

               Q₀=(x-2)²-4;

                  ;

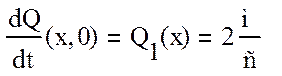- граничные условия, описывающие изменение колебаний на концах струны:

                g₁(t)=0;

                 g₂(t)=0.

            Произведем выверку размерности:

            Пусть Q(x,t) – ортогональное отклонение струны [м]. Тогда входное воздействие f(x,t) имеет размерность [м/с²].

1.2 Расчет статической характеристики

При известной стандартизирующей функции и функции Грина можно найти выходную функцию вычислением интеграла, представляющим собой основное соотношение, связывающее выход объекта при заданном начальном состоянии            с входными воздействиями:

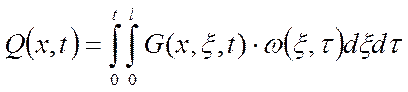                                                                  (1)

        Идентификация исходного уравнения позволяет перейти к расчету распределенной выходной величины, являющейся функцией как пространственной, так и временной координаты, и рассчитываемой как пространственно – временная композиция от произведения функции Грина на стандартизирующую функцию.

Выходная величина Q(x,t) находится как сумма двух составляющих:

Q(x,t)=Q₁(x,t) + Q₂(x,t),                                                                                     (2)

где Q₁(x,t) и Q₂(x,t) находятся как: