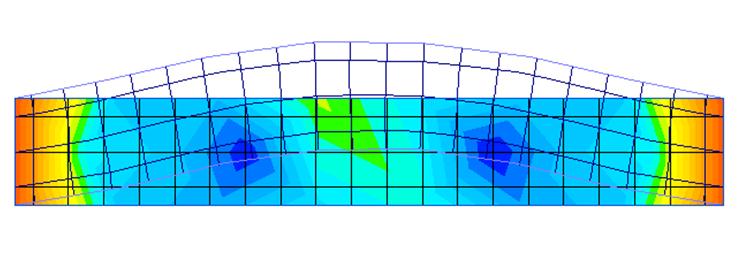
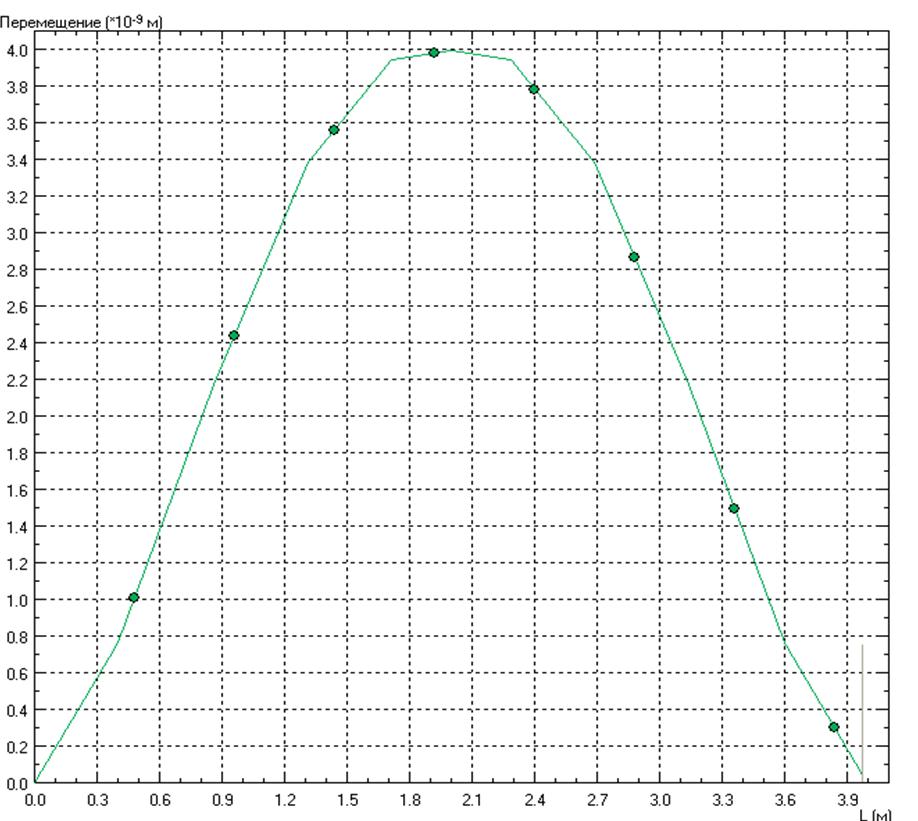
Другие предметы \ Моделирование систем управления

Построение математической модели колебания струны на основе теории распределенных сигналов, страница 3

Струна колеблется от 0 до 4 м.

2 МОДЕЛИРОВАНИЕ НА МАКРОУРОВНЕ

2.1 Исходные данные

Дана схема гидравлической системы, представленная на рисунке 4. В системе используется в качестве рабочей жидкости вверенное масло АУ. Материал трубопровода – сталь. Основные параметры системы и жидкости приведены в таблице 1. Параметры трубопроводов приведены в таблице 2.

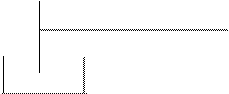Рисунок 4 – Схема гидравлической системы

Расчетная схема гидравлической системы состоит из:

- 1,2,3,4 – потребители выходного расхода;

- насос потока питания 5 с клапаном 6;

- соединяющие магистрали.

Таблица 1 – Параметры системы и жидкости

Обозначение	Основные параметры	Значение
	Плотность рабочей жидкости	860 кг/м³
	Вязкость	0,15·10^-4 м²/с
Е_С	Модуль упругости системы	1,7·10⁸ Па
Е_тр	Модуль упругости трубопровода	10·10¹⁰ Па
	Коэффициент потерь на трение при турбулентном потоке	0,028
	Толщина стенки трубопровода	2,8*10^{-4 м}

Таблица 2 – Параметры трубопроводов

Параметр	Обозначение	Номер трубопровода
Параметр	Обозначение	1	2	3	4	5
Диаметр трубопровода	d_тр, м	0.02	0.03	0.032	0.032	0.015
Длина трубопровода	l,м	1.5	2.5	1.9	1	0.9
Коэффициент местных сопротивлений	ξ	4	5.5	5	5	3
Давление потребителей и насосов	P, *10⁶ Па	0.2	0.25	0.16	0.2	-

Давление потребителей для расчета примем:

P₁ = 0.25*10^-6 м³/с;

P₂= 0.4*10^-6 м³/с.

2.2 Графические формы математической модели гидросистемы

2.2.1 Динамическая схема. На основании исходной принципиальной схемы гидравлической системы (рисунок 4) строится динамическая модель. Участки магистралей представляются как последовательное соединение инерционного и диссипативного элемента, причем для инерционного элемента указывается направление движения рабочей жидкости. В точки ветвления магистралей устанавливают упругие элементы, учитывающие сжимаемость жидкости и деформируемость стенок трубопровода. На рисунке 5 представлена полученная динамическая модель.

2.2.2 Орграф. На основании динамической модели построен ориентированный граф, являющийся графической формой модели гидравлической системы. Узлы орграфа соответствуют сосредоточенным массам, а ветви – компонентам математической модели.

р_в2

Q₂р_в3

Q₁m₂Q₃

μ₂

р_в1 μ₃ m₃ Q₄

р_в4

m₁μ₁μ₄m₄

μ₅

m₅ Q₅c₅

р_н5

Рисунок 5 – Динамическая модель гидравлической системы

Базовый узел (с нулевым номером) отображает инерциальную систему отсчета фазовых координат типа потока. Источник обеспечивает возрастание потоковой переменной узла, поэтому сигналы направляют от базы к узлу. В магистралях потребителей – наоборот. Во всех ветвях инерционных и диссипативных элементов направление сигналов от узла к базе. Такое направление характеризует затраты энергии источников на увеличение кинетической энергии и на трение. В ветвях упругих компонентов стрелки указывают направление передачи энергии от источников к потребителям. В ветвях всех элементов кроме направления записывается параметр каждого элемента. На рисунке 6 представлен полученный орграф.

2.2.3 Матрица инциденций. Для формирования полной математической модели на основе компонентных и топологических уравнений широкое применение получил узловой метод, для него необходимо сформировать матрицу инциденций, отражающую структуру связей всех элементов системы. Матрица инциденций формируется на основании ориентированного графа. Число строк матрицы соответствует числу узлов орграфа, число столбцов – числу ветвей. Отсутствие связи между узлом и ветвью обозначается «0», если ветвь входит в узел – «1», если выходит – «-1».

μ₂

с₅ р_в2μ₃

1 2 3 4 5 6

Скачать файл