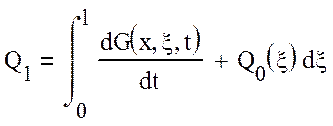Построение математической модели колебания струны на основе теории распределенных сигналов, страница 2

                                                                                        (3)                                                                                  

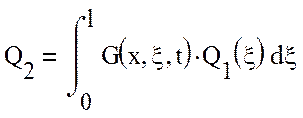                                                                                              (4)

Получим:

(5)

Q(x,t)=Q₁(x,t)+Q₂(x,t)=                     

.

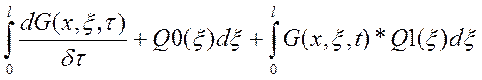
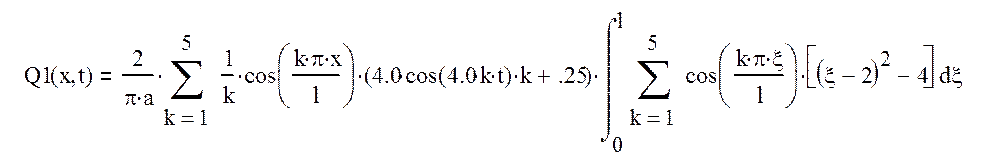Обозначим:

 ;

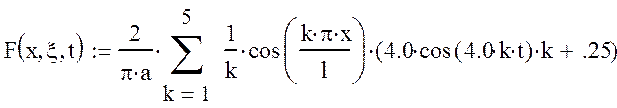тогда:

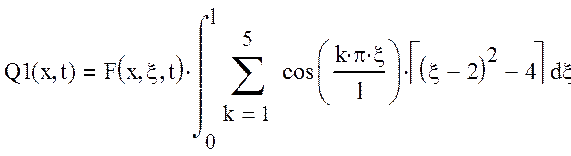.                                                      (6)

       Подставив в уравнения, а=5 и l=4, то есть ограничим длину струны величиной, равной 4м.

Q₁(x,t)=2.1cos(0.79x)cos(4t)+0.13cos(0.79x)+2.1cos(1.6x)cos(8t)+                                                                                                           6.5*10^-2cos(1.6x)+2.1cos(2.4x)cos(12t) 4.3*10^-2cos(2.4x)+2.1cos(3.1x)cos(16t)+ 3.2*10^-2cos(3.1x)+2.1cos(3.9x)cos(20t)+ 2.6*10^-2cos(3.9x)                                                     (7)

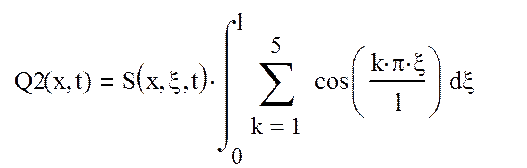.                                           (8)     

где

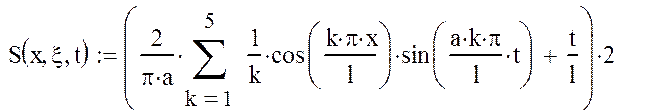
При n=0..5:

            Q₂(x,t)=0.                                                                                                            (9)

            Тогда выходная величина с учетом (7), (9) имеет решение: 

Q(x,t)= 2.1cos(0.79x)cos(4t)+0.13cos(0.79x)+2.1cos(1.6x)cos(8t)+                          6.5*10^-2cos(1.6x)+2.1cos(2.4x)cos(12t) 4.3*10^-2cos(2.4x)+2.1cos(3.1x)cos(16t)+          3.2*10^-2cos(3.1x)+2.1cos(3.9x)cos(20t)+                                                                          2.6*10^-2cos(3.9x)+0 = 2.1cos(0.79x)cos(4t)+0.13cos(0.79x)+2.1cos(1.6x)cos(8t)+                          6.5*10^-2cos(1.6x)+2.1cos(2.4x)cos(12t) 4.3*10^-2cos(2.4x)+2.1cos(3.1x)cos(16t)+  3.2*10^-2cos(3.1x)+2.1cos(3.9x)cos(20t)+ 2.6*10^-2cos(3.9x)                                       (10)

Выражение (10) является статической характеристикой колебания струны. Построим графики выходной распределенной величины в при фиксированных значениях t=0,4 (с) и t= 4(с):

 

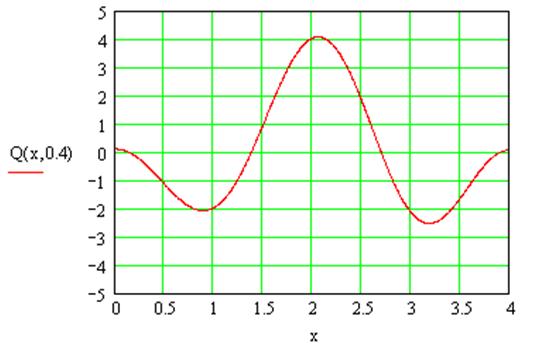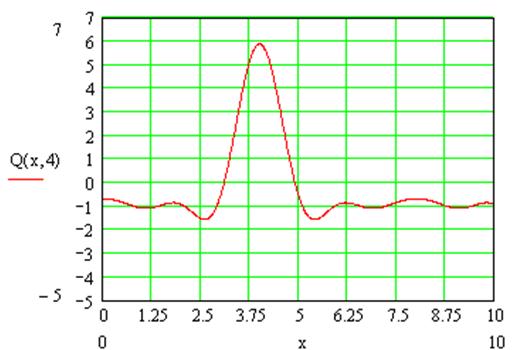Рисунок 1 – Колебание струны при t=0,4c

Рисунок 2 – Колебание струны при t=1 c

1.3 Расчет динамической характеристики

Динамическая характеристика находится по интегральной передаточной функции , которая рассчитывается как пространственная композиция от произведения континуальной передаточной функции  на преобразованную по Лапласу стандартизирующую функцию  с выделенным из нее входным воздействием. Так как стандартизирующая функция не содержит входное воздействие f(x,t):

           ;                                 (11)

       ω(ξ,p)=L{((ξ-2)²-4))*δ’(t)}+L{2* δ(t)}= ((ξ-2)²-4)*p+2                                   (12)                                         

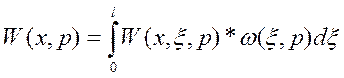                                                                                      (13)                                                               

     Интегральную передаточная функция запишется в виде:

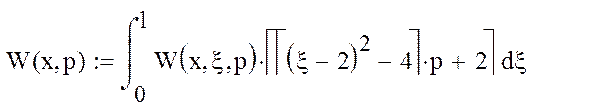                                              (14)                                                                                                                                

Подствавим в выражение исходные данные и найдем интегральную передаточную функцию в точке x=1, ограничив количество членов ряда до 5:

 

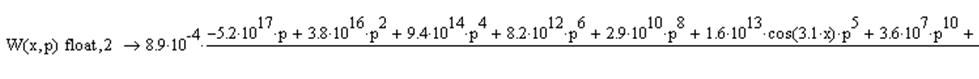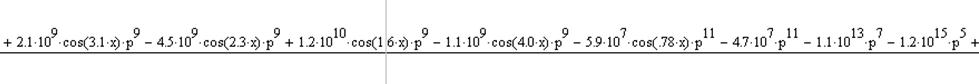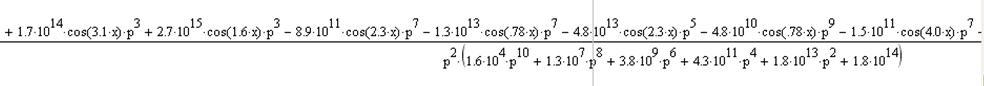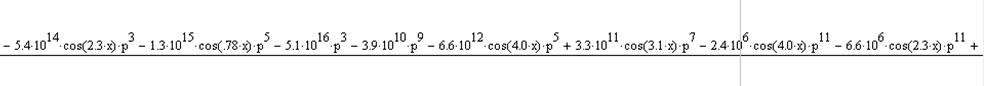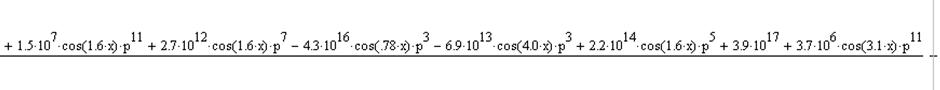                                                                                                                         (15)

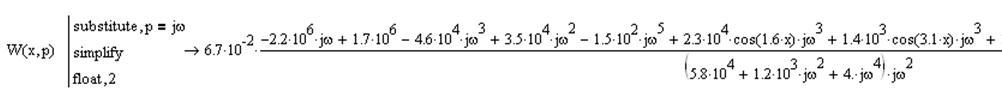         При замене p на jω получим выражение для частотной передаточной функции:

 

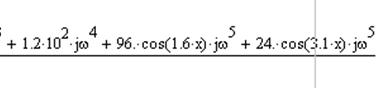                                                                                                                                    (16)                                                                                                                                                                       

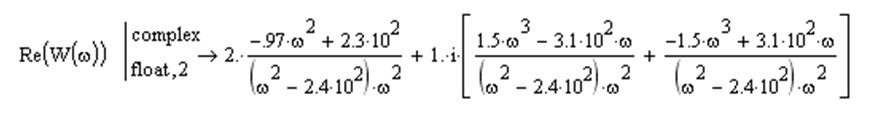         Выделим действительную и мнимую части:

                                                                                                                                    (17)

 

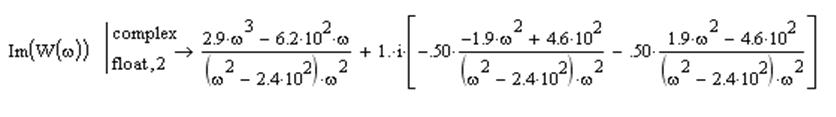                                                                                                                                               (18)                                                                                                                         

Найдем  ЛАЧХ по выражению:

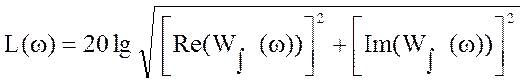.                                                        (19)

Для построения характеристики используем программу MathCad:

                                                       

                                                       -40дб/дек

                                                                                   - 20дб/дек

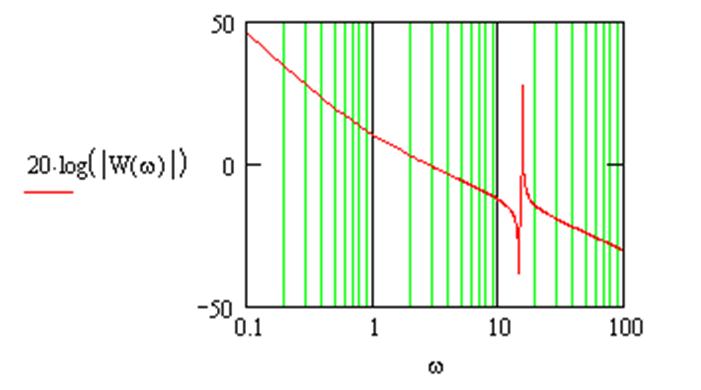
Рисунок 3 – График логарифмической амплитудно-частотной характеристики

Аппроксимируя полученную ЛАЧХ ее стандартными типовыми наклонами получаем -40 дб/дек и -20 дб/дек, что соответствует апериодическому звену 2-го порядка. Тогда передаточная функция будет иметь вид:

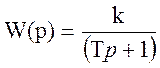;                                                                (20)

найдем Т, при условии:T=1/ ω1,

где Т - период, с.

ω - частота аппроксимированной ЛАЧХ, Гц.

T=1/ ω1= 1/0,9=1,11 (с).

            График ЛАЧХ пересекает ось Y в точке 8, тогда усиление равно:

20lgk = 8, откуда k=10^8/20=2,512                                                                    (21)

С помощью аппроксимации передаточная функция запишется в виде:

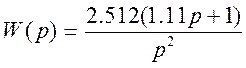                                                              (22)

1.4  Моделирование струны в среде Elcut

Смоделируем колебания струны при граничных условиях g₁=0, g₂=0. Построим двумерную модель струны в виде прямоугольника длиной l=4м и высотой h=0,6 м, зададим значения граничных условий на ребрах модели и выберем свойства материала стержня (медь электротехническая). Решение задачи получим в виде цветовой шкалы, а также графика колебаний: