Построение математической модели колебания струны на основе теории распределенных сигналов, страница 4

                                  1                  р_в1                 m₂                                       3

                                                       m₁                                         m₃

                                               μ₁                                                    р_в3

                                                  р_н5     m_{5             0}                    m₄          μ₄

                                                                   μ₅            р_в4                      4       с₅

                                         5   

Рисунок 6 – Ориентированный граф гидравлической системы

Матрицу инциденций А можно представить состоящей из подматриц инерционных А_И, диссипативных А_Д, упругих А_У ветвей и подматрицы ветвей источников потенциалов А_В. Для исходной системы получена матрица, представленная в таблице 3:

А=[A_И, А_Д, А_У, А_В]                                                                                        (23)

Таблица 3 – Матрица инциденций гидравлической системы

Узлы	Ветви
	Диссипативные коэффициенты					Упругие коэффициенты	Внешние воздействия
	μ1	μ2	μ3	μ4	μ5	с5	рв1	рв2	рв3	рв4	рн5
1	-1	0	0	0	0	1	-1	0	0	0	0
2	0	-1	0	0	0	1	0	-1	0	0	0
3	0	0	-1	0	0	1	0	0	-1	0	0
4	0	0	0	-1	0	1	0	0	0	-1	0
5	0	0	0	0	-1	-1	0	0	0	0	1
Подматрица	Ад					Ау	Ав

2.3 Узловой метод формирования математической модели гидросистемы

Из матрицы инциденций можно получить систему равнений (24), математически описывающие функционирование гидравлической системы:

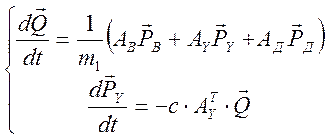                                                                       (24) где ;

А_Д, А_У, А_В – подматрицы инциденций;

 - векторы давлений;

- векторы расходов,

       m, с,  - диагональные матрицы параметров элементов гидравлической системы.

Для нашего случая система будет иметь вид:

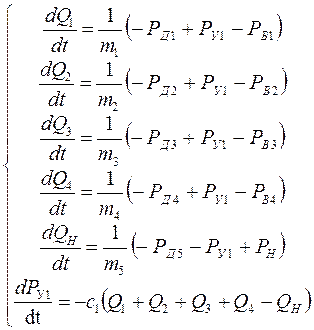                                                                           (25)                                                                        

 Так как в исходной системе насос постоянной производительности, то 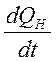=0 и пятое уравнение (25) преобразуется к виду:

 P_H = P_Д5 + P_У1                                                                                                (26)                                                                                                                                                                                                                                                                                                                                                                                                         

Комплексные уравнения диссипативных элементов носят более сложный характер, при этом выделяют линейные и нелинейные потери давления в гидромагистралях и уравнения  запишется в следующем виде:

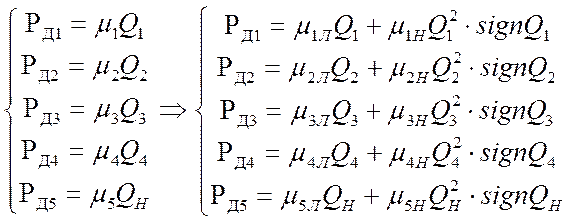                                    (27)

где, коэффициент гидравлического сопротивления, характеризующий линейные потери при ламинарном режиме движения жидкости;

коэффициент гидравлического сопротивления, характеризующий нелинейные потери при турбулентном режиме, по длине и местные.

Таким образом, математическая модель рассматриваемой гидросистемы представляется системой пяти дифференциальных уравнений и шестью алгебраическими выражениями.

Вычисление параметров трубопровода гидросистемы

Значения коэффициентов линейных и нелинейных потерь для конкретной магистрали находят по формулам:

-площадь сечения трубопровода, м²:

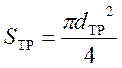;                                                                                                      (28)

-коэффициент линейных потерь, H·с/м⁵;

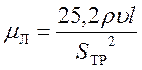;                                                                                                   (29)

       -коэффициент нелинейных потерь, H·с/м⁵.

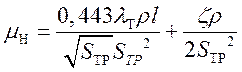 ;                                                                                                 (30)

-коэффициент жесткости участка:

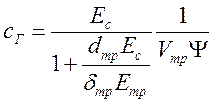 ;                                                                                        (31)

где - доля объема трубопровода;

-объем трубопровода, м³:

V_тр=S_тр·l .                                                                                                         (32) Доля объема трубопровода рассчитывается как отношение объема отдельного участка к сумме объемов всех n соединенных между собой участков:

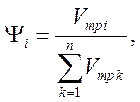                                                                                                     (32)

где  - объема трубопровода i-ого участка, м³.

       Коэффициент жесткости упругого элемента:

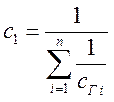.                                                                                                        (34)

По исходным данным и полученным результатам получаем жесткость упругого элемента c₁= 2,258·10¹¹ Н/м⁵.

Коэффициент массы:

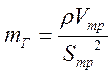.                                                                                                        (35)

Полученные результаты для отдельных участков трубопровода приведены в таблице 4.

Таблица 4 – Параметры трубопровода гидросистемы