Построение математической модели колебания струны на основе теории распределенных сигналов, страница 5

Параметр	Номер магистрали
	1	2	3	4	5
Площадь сечения трубопровода, Sтр, ·10-4 м2	3,142	7,069	8,042	8,042	1,767
Объем трубопровода, Vтр,·10-4 м3	4,712	17,67	15,28	8,042	1,59
Доля объема трубопровода,	0,047	0,177	0,153	0,08	0,016
Коэффициент массы, mг,·106 кг/м4	4,106	3,042	2,032	1,069	4,38
Коэффициент линейных потерь,,·106 H·с/м5	4,941	1,627	9,549	5,026	9,369
Коэффициент нелинейных потерь,,·1010 H·с/м5	2,657	0,674	0,442	0,39	6,444
Коэффициент жесткости участка, cг, ·1010  Н/м5	682,6	46,05	60,96	220,1	6160

2.4 Расчет статической модели гидросистемы

При постоянном воздействии система находится в установившемся равновесном состоянии. Ее фазовая координата (давление Р и расход Q) при этом постоянна. Такой режим функционирования системы называется статическим и достигается при постоянном внешнем воздействии:

– давления к потребителю (Р_В1, P_В2, P_В3, P_В4),

– подачи насоса Q_H.

При этом устанавливаются постоянные значения фазовых координат системы:

– расход в гидромагистралях,

– давление в упругом элементе.

Из данного утверждения следует:

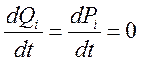                                                                                                     (36)

Из (24) и (26) получаем систему для статического режима:

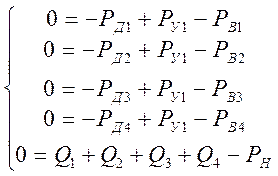                                                                                 (37)

Учитывая нелинейные свойства диссипативных элементов гидравлической системы, их компонентное уравнение имеет вид:

                                                                                   (38)

Перенесем в правую часть системы внешние воздействия, тогда статическая модель будет иметь вид:

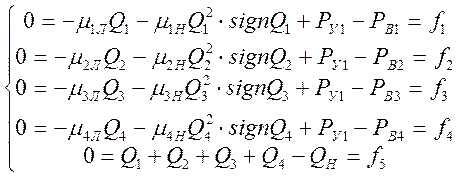                                                       (39)

Для ее решения используются численный метод, для которого предварительно сформируем матрицу Якоби. Элементами матрицы Якоби для сформированной нелинейной системы являются частные производные от нелинейной вектор-функции  по фазовым координатам системы (Q₁, Q₂,Q₃,Q₄,Q_н, P_У1).

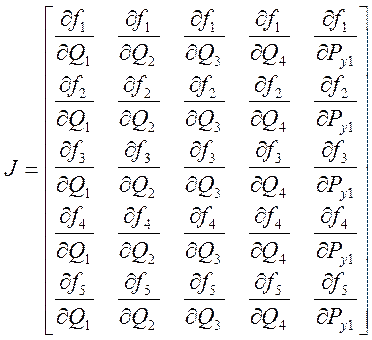                                                                    (40)

Нахождение частной производной по расходу от давления в диссипативном   элементе (38) имеет вид:

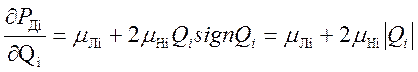                                                             (41)

Матрица Якоби исходной гидросистемы имеет вид:

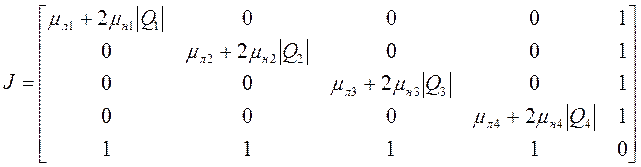                             (42)

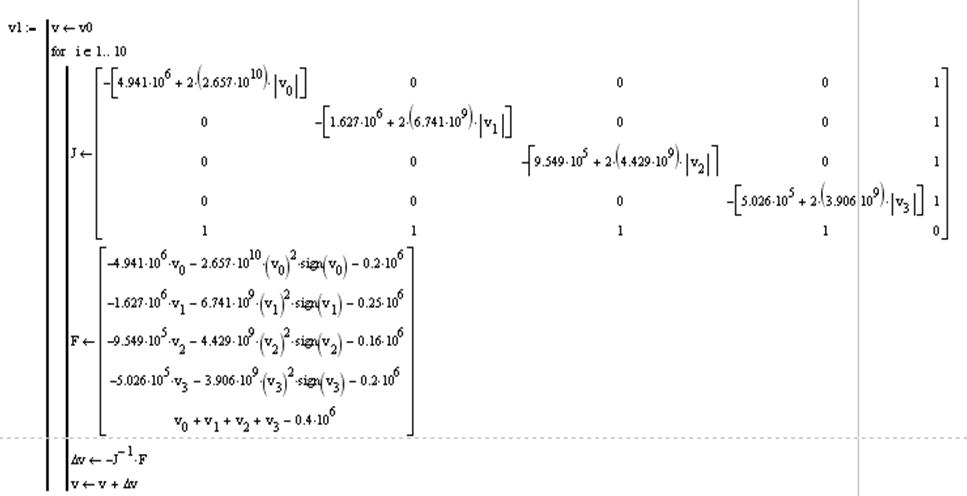
тогда матрица (42) принимает вид:

 

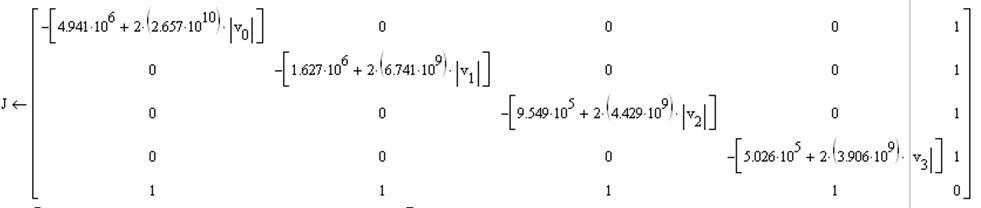Для решения статической модели используем численный метод Ньютона, алгоритм которого включает следующие этапы:

– выбор начального приближения , где  - вектор фазовых координат (Q₁, Q₂, Q₃, Q₄, P_У1), V₀ – нулевой вектор-столбец;

– вычисление матрицы Якоби J_k в точке _K (k=0, 1, 2 …);

– вычисление вектора невязок . Вектор невязок получается из системы уравнений (27) для статического режима:

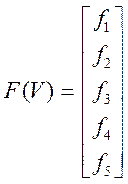                                                                                                       (43)

–  определение вектора поправок:

.                                                                                            (44)

– определение нового приближения вектора искомых фазовых переменных:

.                                                                                                                 (45)

– проверка условия окончания итерационного процесса, при выполнении условия, что V_k и V_k+1 соизмеримы (совпадают до десятых), иначе происходит переход на предыдущие этапы и вычисляется следующая итерация.

Расчет фазовых координат при статическом процессе произведен в математическом пакете MathCad.

Решением является матрица:

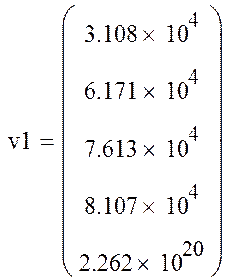                                                                                                    (46)

 

При Q_H = 0,4*10⁶ м³/с решением является матрица:

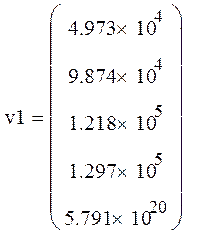                                                                                                           (47)                                                                                                      

 

Результаты вычислений приведены в таблице 5:

Таблица 5 – Результаты статического анализа

Фазовая координата	при Qн=50*10-6, м3/с	при Qн=300*10-6, м3/с
Q1, м3/с	-1,343*10-3	-1,347*10-3
Q2, м3/с	-3,795*10-3	-3,8*10-3
Q3, м3/с	3,965*10-3	3,915*10-3
Q4, м3/с	1,123*10-3	9,316*10-4
Pу1, Па	1,508*106	1,504*106

2.5 Анализ динамической модели гидросистемы

Динамическая модель описывает переходный процесс гидросистемы. В общем случае система дифференциальных уравнений, описывающих гидравлическую систему, имеет вид:

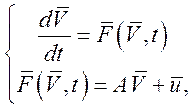                                                                                           (48)

где А – матрица Якоби,

 - вектор фазовых координат,

 - вектор-функции внешних воздействий,

 - вектор функции внешних воздействий.

С учетом произведенных ранее расчетов, запишем систему дифференциальных уравнений, представляющую динамическую гидросистему:

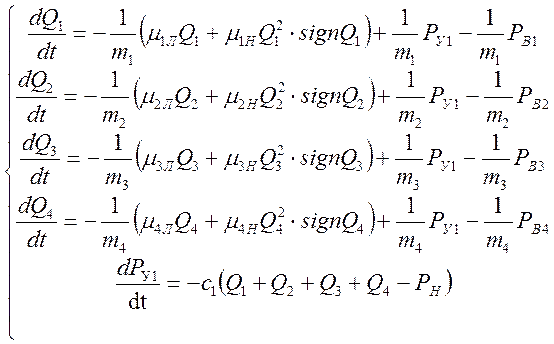                                             (49)

Для динамической модели матрицу Якоби можно аналогично статической модели:

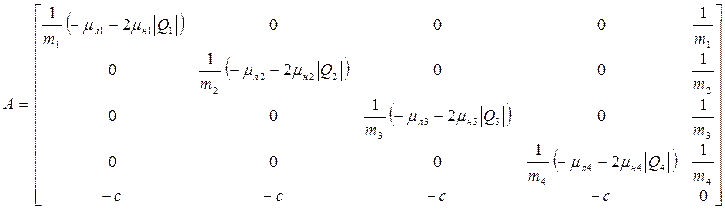                     (50)

Переходный процесс определяется в результате численного интегрирования системы (49), для чего необходимо произвести выбор ряда параметров.

Пусть  переходный процесс оценивается как реакция системы, находящейся в состоянии покоя, на ступенчатое воздействие вида:

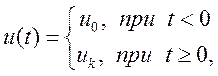                                                                                          (51)