Системы, состояния которых описывается функциями нескольких алгоритмов, зависящих как от времени, так и от пространственных координат, получили название СРП.
Основные особенности СРП
1) Состояние СРП описывается дифференциальным
уравнением в частных производных (содержащие производные функции состояния, как
во времени, так и по пространственным координатам), интегральными уравнениями,
а также гибкими системами уравнений различной природы ![]() математические
модели СРП качественно отличаются от ССП.
математические
модели СРП качественно отличаются от ССП.
2) По сравнению с ССП расширяется класс управляющих воздействий за счет пространственно-временных управлений, описываемых подобно управляемому состоянию СРП, функциями нескольких аргументов (t,x), применительно к таким воздействиям становится непригодные стандартные техники исследования ССП.
Базовая функция объектов с распределенными параметрами
Функция состояния Q(x,t) объекта с распределенными параметрами (вход объекта),
определенная по пространственной переменной ![]() (замкнутой
области D), удовлетворяют уравнению:
(замкнутой
области D), удовлетворяют уравнению:
![]()
![]()
![]() (1)
(1)
где
![]() - открытая часть области D, не
содержащая границы.
- открытая часть области D, не
содержащая границы.
L – некоторый заданный оператор (линейная функция Q, в частных производных Q(x,t) различных порядков, интегральный оператор от Q(x,t) и/или x, t).
Конкретный вид L определяется содержанием описываемого процесса.
f(x,t) – известная функция, характеризующая внешнее воздействие на процесс (вход ОРП).
Если ![]() , то уравнение
(1)однородное, соответственно, если
, то уравнение
(1)однородное, соответственно, если ![]() , то уравнение
(1) – неоднородное.
, то уравнение
(1) – неоднородное.
Замечание 1:
Если ![]() - векторная
функция состояния,
- векторная
функция состояния, ![]() , где
, где ![]() , то уравнение (1) представляет собой
систему n-операторных уравнений.
, то уравнение (1) представляет собой
систему n-операторных уравнений.
Далее будим считать, что ОРП описывается единственным
уравнением (1) для одной функции ![]() .
.
Замечание 2:
В большинстве практических задач L – это дифференциальный оператор. Для единственного решения необходимо его дополнить начальными условиями, которые описываются некоторым линейным оператором N.
![]()
![]()
![]() (2)
(2)
При заданных начальных условиях ![]() , описывающих распределение в D,
состояние ОРП в начальный момент времени. Если
, описывающих распределение в D,
состояние ОРП в начальный момент времени. Если ![]() ,
то начальное условие (2) называется нулевым. Если
,
то начальное условие (2) называется нулевым. Если ![]() ,
то начальное условие (2) называется не нулевым.
,
то начальное условие (2) называется не нулевым.
Условие (2) необходимо, но недостаточно для выделения единственного решения, что является важной принципиальной особенностью РСП по сравнению с ССП.
Полная система соотношений должна содержать граничные
условия, для ![]() , которые характеризуют
взаимодействие
, которые характеризуют
взаимодействие ![]() с внешней средой, должны
выполняться для
с внешней средой, должны
выполняться для ![]() на границе
на границе ![]() области
области ![]() .
.
![]()
![]()
![]() (3)
(3)
где Г – линейный оператор,
![]() - внешнее
воздействие, которое можно рассматривать как второй вход объекта наряду
- внешнее
воздействие, которое можно рассматривать как второй вход объекта наряду ![]() .
.
Если ![]() , то граничные
условия однородные. Если
, то граничные
условия однородные. Если ![]() , то граничные
условия неоднородны.
, то граничные
условия неоднородны.
Уравнения (11)-(13) с заданными линейными
дифференциальными операторами L, N, Г, составляющие краевую задачу, являются базовой
моделью для математического описания широкого класса ОРП с управляющей выходной
функцией состояния ![]() и внешними входами
и внешними входами ![]() и
и ![]() ,
которые могут фигурировать как в качестве управляющих, так и/или возникающих
воздействий.
,
которые могут фигурировать как в качестве управляющих, так и/или возникающих
воздействий.
Иногда в качестве входа объекта выступает начальная
функция ![]() .
.
Замечание:
Далее рассматриваются только детерминированные модели.
Функция состояния ![]() ОРП
представляет собой большинство случаев пространственно-временные характеристики
полей различной физической природы, и поэтому с удовлетворительной точностью
описываются линейные диффиринциальные уравнения.
ОРП
представляет собой большинство случаев пространственно-временные характеристики
полей различной физической природы, и поэтому с удовлетворительной точностью
описываются линейные диффиринциальные уравнения.
Чаще всего уравнение математической функции имеет порядок не выше второго (по номеру старшей производной).
Для простейшего случая пространственной
распределённости по одной координате х, изменяющейся на отрезке ![]() (одномерная задача), уравнение (1) записывается
в виде:
(одномерная задача), уравнение (1) записывается
в виде:
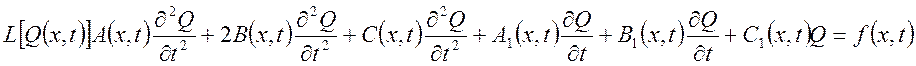 (4)
(4)
где А, В, С – заданные функции могут быть равны CONST/
В зависимости от значения, дискриминанты Δ, равные (АВВ2), различают уравнения:
- гиперболического типа (Δ<0),
- параболического типа (Δ=0),
- эллиптического типа (Δ>0),
- смешанного типа (Δ меняет знак в области допустимых изменений x и t).
Уравнения гиперболического типа
Уравнения содержат две производные функции состояния, как по t, так и по x, они описывают колебательные процессы различной природы (механические, электромагнитные, звуковые и т.д.), связанные с конечной скоростью V, распространения волновых явлений.
1) ![]()
![]()
![]()
![]()
![]()
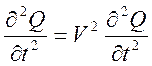
![]()
![]()
![]() (5)
(5)
Уравнение (5) моделирует распространение свободных
колебаний (при распространении со скоростью звука ![]() пульсации
расхода газа в длинном трубопроводе).
пульсации
расхода газа в длинном трубопроводе).
При ![]() , уравнение (5)
записывается в виде:
, уравнение (5)
записывается в виде:
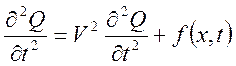
![]()
![]() -
описывает вынужденные
-
описывает вынужденные
колебания под влиянием
внешнего воздействия ![]() .
.
Лекция № 8
2) Уравнение гиперболического типа:
![]()
![]()
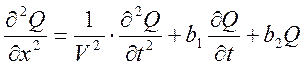
![]()
![]()
![]() (7)
(7)
Описывает распределение напряжения тока вдоль длинной электрической линии.
![]() - скорость
распределения электромагнитных волн вдоль линии.
- скорость
распределения электромагнитных волн вдоль линии.
При ![]() уравнение (7)
сводится к волновому уравнению, при
уравнение (7)
сводится к волновому уравнению, при ![]() и
и ![]() уравнение (7) моделирует процессы механических
колебаний в среде сопротивления.
уравнение (7) моделирует процессы механических
колебаний в среде сопротивления.
Уравнение параболического типа
Они содержат первую производную 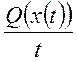 и вторую производную по координате t.
и вторую производную по координате t.
Описывает задачи, связанные с процессами теплопроводности, диффузии с распространением электромагнитных волн, с движением вязкой жидкости и т.д.
Уравнение теплопроводности (уравнение Фурье)
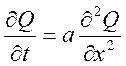
![]()
![]()
![]() (8)
(8)
Уравнение (8) – однородное уравнение теплопроводности, описывает температурные поля не стационарной теплопроводности, тепло массы перевода и т.д.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.