Моделирование. Математические схемы моделирования. Основные подходы к построению математической модели системы. Дискретно детерминированные системы (F-схемы), страница 2

В общем случае все переменные являются элементами подмножеств и содержат как детерминированные, так и стохастические состояния.

То есть, имеем следующую систему:

Экзогенные (независимые)

	Эндогенные (зависимые переменные)

 

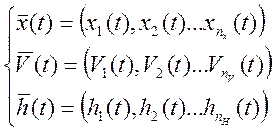
Процесс функционирования систем S в общем случае описывается во времени операторам F_S , который преобразует экзогенную переменную и эндогенную.

Для динамических систем:

                                                                                                         (1)

Совокупность зависимостей выходных характеристик системы во времени y_i(t), , называется выходной траекторией, т.е. формула (1) называется законом о функционировании системы и позволяет получить выходную траекторию системы.

Закон функционирования F_S может, задан в виде функций логических условий в алгоритмических или табличных формах, в виде словесного описания.

Алгоритм функционирования A_S – это метод получения выходных характеристик, с учетом входных воздействий , воздействий внешней среды   и собственных параметров системы .

Один и тот же закон функционирования F_S может быть реализован различными способами, т.е. с помощью различных алгоритмов A_S.

Для описания статических моделей:

                                                                                                           (2)

Соотношение (1)  и (2) может быть задано различными способами, например, в ряде случаев могут быть  получены через свойства системы S в конкретные моменты времени, называемые состоянием системы.

Состояние системы характеризуется векторами:

,

,

где  

,

,

,

,

в момент

,

,

,

и т.д., при

Если рассматривать процесс функционирования системы S как последовательность смен состояний , то они могут быть интерпретированы как коэффициенты точки к-мерной базового пространства, причем каждая реализация соответствует некой фазовой траектории.

Совокупность всех возможных значений состояний , называется пространством состояний, причем .

Состояние системы S в момент времени полностью определяется начальными условиями, выходными воздействиями , внутренними параметрами  и воздействиями внешней среды , которые имели место за промежуток времени от  до  и описывается, с помощью следующих уравнений.

,

где

,

,

.

                                                                                                            (3)

                                                             .                                                           (4)

Первое уравнение (3) по начальному состоянию  и независимым переменным  определяют вектор функции , а уравнение (4) по полученному значению состоянию  определяет зависимые переменные на выходе . Таким образом, цепочка уравнений объекта вход → состояние → выход, позволяет определить характеристику системы, описываемую уравнением (5).

                                                                                                   (5)

В общем случае время в модели системы S может рассматриваться на интервале моделирования от 0 до Т, как непрерывное, так и дискретное, т.е. квантованное на отрезке  временных единиц каждой, тогда Т выражается , где  - число интервалов дискретизации.

Непрерывно детерминированные модели (D-схемы)

Используя этот подход в качестве математической модели, применяют диффиринциальные уравнения.

Если в диффиринциальных уравнениях не известны функции многих переменных, то уравнение называется дифференциальным уравнением в частных производных. В противном случае, при рассмотрении функции только одной независимой переменной, называется обыкновенным дифференциальным уравнением.

Математическое состояние для детерминированных систем будет выглядеть:

,

,

где 

,

,

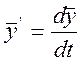 - вектор функция, которая определена на некотором (n+1)-мерном множестве и является непрерывной, т.к. математические схемы такого вида отражают динамику изучаемой системы, то они называются D-схемами.

Лекция № 3

Наиболее важно для системотехники приложение D-схем, в качестве математического аппарата в ТАУ.

Для иллюстрации рассмотрим две элементарные системы различной физической природы.

а) Механическая – колебание маятника.

 

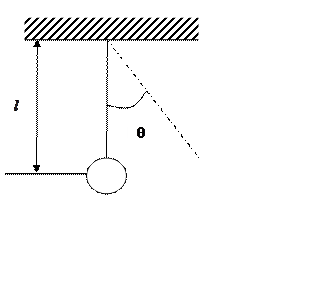
Процесс малых колебаний маятника описывается обыкновенным дифференциальным уравнением вида:

,

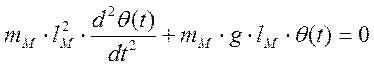где   - масса маятника;

 - длина подвеса маятника;

 - ускорение свободного падения;

 - угол отклонения маятника в момент времени t.

Из этого уравнения могут быть получены различные характеристики, например, период колебания маятника:

.

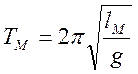б) электрический контур.

Аналогичны процессы в электрическом контуре, описывается дифференциальное уравнение вида:

,

.

 

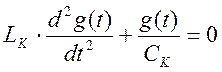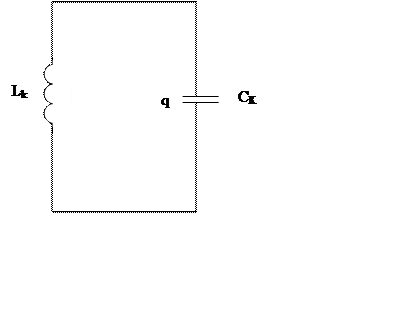где    и  - индуктивность, и емкость конденсаторов,

 - заряд конденсатора в момент времени t.

Из этого уравнения также могут быть найдены различные характеристики, например, .

Очевидно, что, введя обозначения: , , , , , 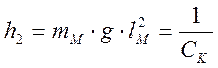получим дифференциальное уравнение второго порядка:

,

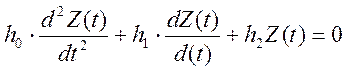где   - параметры системы;

 - состояние системы в момент времени t.

Таким образом, поведение этих двух объектов может быть исследовано на основе общей математической модели, причем поведение одной системы может быть проанализировано с помощью другой и наоборот.

Если изучаемая система маятника или контур взаимодействует с внешней средой, то появляется входное воздействие x(t) (внешняя сила для маятника и источник энергии для контура). Тогда непрерывно детерминированная модель будет иметь вид:

.

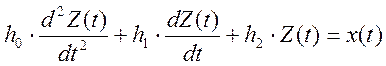Получение передаточной функции из дифференциального уравнения

Передаточная функция равна отношению изображений по Лапласу переменных выходов и входа при нулевых начальных условиях.

Пусть система описывается дифференциальным уравнением второго порядка:

.

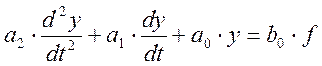Начальные условия:  и .

Преобразуем уравнение по Лапласу, для чего воспользуемся свойством линейности преобразования, а также теоремой о дифференцирования оригинала.