Моделирование. Математические схемы моделирования. Основные подходы к построению математической модели системы. Дискретно детерминированные системы (F-схемы), страница 4

Xi	ZK
	Z0	Z1	Z2
	Переходы
X1	Z2	Z0		Z0
X2	Z0	Z2	Z1
	Выходы
X1	y1	y1	y2
X2	y1	y2	y1

 

,

,

.

При другом способе задания автомата используется понятие направленного графа.

Граф автомата представляет собой набор вершин, соответствующие различным состояниям автомата и соединяющих вершины дуг графа, соответствующие тем или другим переходам автомата.

 

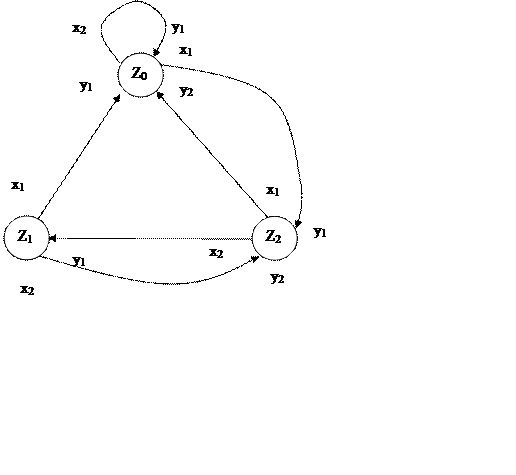При матричном задание конечного автомата записывается квадратная матрица , строки которой соответствуют исходным состоянием, а столбцы состоянием перехода. Элемент , стоящий на пересечении i-той строки и j-того столбца в случае автомата Мили соответствует входному сигналу Х_К, вызывающему переход из состояния Z_i в состояние Z_j и выдаваемые при этом в переходе.

Пример: для нашего случае.

.

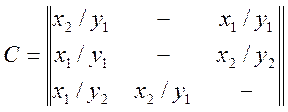Дискретно стохастические модели

Или Р-схемы описываются с помощью вероятностных автоматах (probabilistic automat).

В общем, виде вероятностный автомат можно определить преобразователь с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть записана статическими.

Введем понятие Р-автомата.

G – множество пар (х_i, Z_S), где х_i - элементы входного множества х;

Z_S – элементы подмножеств S;

Y – выходное подмножество;

В – подмножество вероятности переходов в состояние Z_K и появления на выходе y_j, если автомат был в состоянии Z_S и на вход поступил сигнал x_i.

.

Тогда схема Р, описывающая все перечисленные подмножества , называется вероятностным автоматом.

Как и в случае F-схемы существуют Р автоматы Мили и Мура.

Частотным случаем Р-автомата являются автоматы, у которых переход либо в новое состояние, либо выходной сигнал определяются детерминированием.

 В первом случае автомат носит название Z- детерминированный вероятностным автоматом, во втором случае Y- детерминированный Р-автомат.

Для оценки различных характеристик исследуемых систем представляемых в виде Р-схем используются как аналитические модели, основанные на теории Марковских цепей, так и имитационные модели это метод статического моделирования.

Лекция № 5

Непрерывно стохастические модели (Q-схемы)

Особенностями непрерывно стохастических моделей рассмотрим на примере систем массового обслуживания, которые представляют собой класс математических схем, разработанных теорией управления массовыми процессами.

Основные состояния. В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем. При этом характерным для работы таких объектов является случайное появление заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени, т.е. имеет место стохастический процесс функционирования систем.

В любом элементарном процессе обслуживания можно выделить две особенных составляющих: ожидание обслуживания и само обслуживание.

Это можно изобразить в виде некоторого i-того прибора обслуживания.

  

.

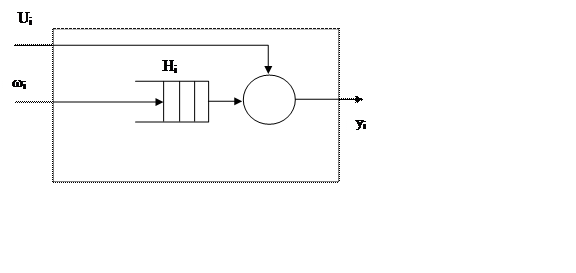
Прибор обслуживания Р_i состоит из накопителя заявок N_i, в котором может одновременно находиться  заявок.

L_i– емкость i-того накопителя и канала обслуживания заявок K_i.

На каждый элемент прибора поступают потоки событий, в накопитель поток заявок ω_i, на канал поток обслуживания U_i.

Потоком событий называется последовательность событий, происходящих одно за другим в случайные моменты времени.

Поток событий называется однородным, ели он характеризуется только моментами времени поступления данных  событий, которые называются вызывающими моментами. Такой поток задается последовательностью t_n.

,

где  t_n– момент наступления n-ного события, причем t_n­ не отрицательное вещественное число.

Однородный поток может быть также задан в виде последовательности промежутков времени между n-ным и (n-1) событием. Такая последовательность обозначается τ_n, которая одназначна с последовательностью вызывающих моментов t_n.

Поток неоднородных событий называется последовательность , где t_n – вызывающие моменты, f_n– набор признаков события.

Применительно к элементарному каналу K_i, можно считать:

1. Поток заявок ω_iпринадлежит множеству заявок W, т.е. интервалы между моментами появления заявок образует подмножество неуправляемых переменных.

2. Поток обслуживания u_i принадлежит множеству U, т.е. интервал времени между началом и окончанием обслуживания заявок образует подмножество управляющих переменных.

3. Заявки, обслуживание каналом и заявок, покинувших прибор по различным причинам образует выходной поток , т.е. интервал времени между моментами выхода заявок образуют подмножество выходных переменных.

4. Процесс функционирования прибора обслуживания P_i можно представить, как процесс изменения его состояния во времени.

Время, за которое происходит изменение состояния объекта, обозначим через Z_i.

Переход в новое состояние для прибора означает изменение количества заявок, которые в нем находятся в канале и накопителе. Таким образом, вектор состояния для прибора P_iбудет иметь вид:

,

где    - состояние накопителя ( - наполнитель пуст,  - накопитель полностью заполнен),

 - состояние канала ( - канал пуст,  - заполнен).

В практиках моделирования систем, имеющих более сложные структуры связи и алгоритм поведения, используют Q-схемы, образуемые композицией многих элементарных приборов обслуживания. Если каналы К различных приборов соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема).

Если приборы соединены последовательно, то имеет место многофазное обслуживание, многофазная Q-схемы.