Метод фазовой плоскости

Метод фазовой плоскости

I.  Общие понятия

Метод фазовой плоскости применяется для исследования систем, описываемых дифференциальными уравнениями не выше второго порядка (в принципе можно применить этот метод и для систем более высокого порядка, но в этом случае получается фазовое пространство, метод теряет наглядность).

Метод фазовой плоскости позволяет оценивать поведение НСАР в любой момент времени при любых начальных условиях. Он может быть применим к НСАР с любыми нелинейностями, однако мы ограничимся случаем кусочно-линейной нелинейности. В этом случае уравнение нелинейной САР представляет систему линейных уравнений второго порядка вида:
(1)               

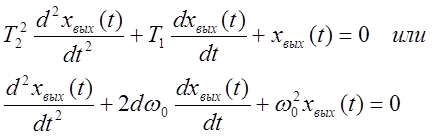
где 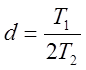 – коэффициент затухания;  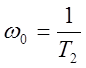– частота собственных колебаний.

Идея метода фазовой плоскости заключается в том, что из дифференциального уравнения исключается время, а поведение системы оценивается по расположению некоторой точки в определённой системе координат, характеризующей состояние системы.

В качестве координат фазовой плоскости чаще всего выбирают выходную величину ; и её первую производную по времени .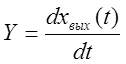

Величины полностью определяющие состояние системы называются её координатами. Плоскость с координатами системы (координатная плоскость) называется фазовой плоскостью. Точка фазовой плоскости, отображающая состояние системы в определённый момент времени, называется изображающей точкой системы. Траектория, описываемая изображающей точкой при изменении состояния системы (геометрическое место изображающих точек), называется фазовой траекторией.

Фазовая траектория даёт полное представление о характере процесса в САР. Если САР устойчива, фазовая траектория стремится к нулю, т.к. в этом случае  и 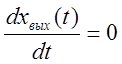. В случае неустойчивой системы фазовая траектория уходит в бесконечность.

Свойства фазовой траектории

1.  Фазовые траектории не пересекаются, т.к. их пересечение означало бы, что одним и тем же начальным условиям соответствует несколько решений дифференциального уравнения.

2.  Фазовые траектории проходят всегда по часовой стрелке. (Рис. 1)

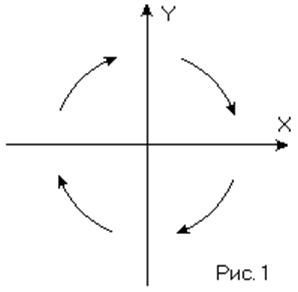
Пусть 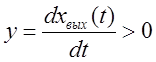, следовательно растёт, а для этого изображающая точка должна двигаться слева направо.

Совокупность фазовых траекторий при различных начальных условиях образует фазовый портрет системы.

Найдём уравнение возможных фазовых траекторий для дифференциального уравнения (1)

Введём обозначение:

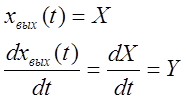           (2)

Уравнение фазовой траектории будем искать в виде

В соответствии с обозначениями (2) уравнения (1) перепишем в виде:
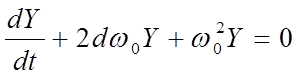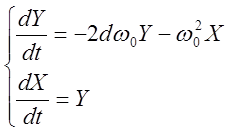, или             (3)

Поделив первое выражение (3) на (2), получим уравнение фазовой траектории

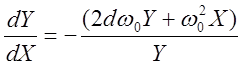          (4)

Уравнение (4) является дифференциальным уравнением фазовой траектории. Решая его, можно построить фазовые траектории. В тех случаях, когда это сложно, применяют метод изоклин.

II.  Метод изоклин

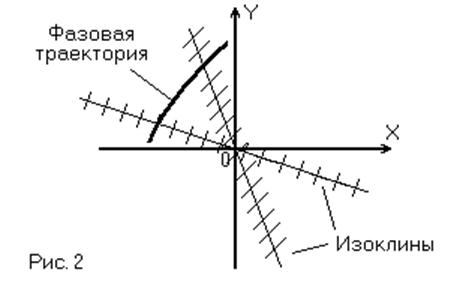
Кривая, соединяющая все точки фазовой плоскости, в которых касательные ко всем фазовым траекториям имеют одинаковый угол  с осью абсцисс, называется изоклиной. (Рис. 2)

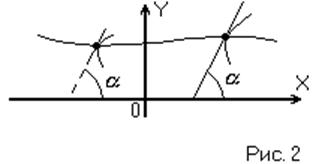
Уравнение изоклины:

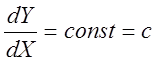,  (5)

где

Сопоставляя (5) и (4), имеем  или

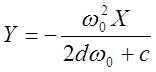,      (6)

т.е. изоклины в данном случае – прямые линии проходящие через начало координат. Для облегчения построения фазовых траекторий изоклины предварительно наносятся на чертёж с чёрточками, обозначающими наклон касательных. (Рис. 3)

Из выражений (6) следует, что вид изоклин, а значит и фазовых траекторий зависит от величины d – коэффициента затухания, т.е. от вида корней характеристического уравнения (1)

    (7)

III. Фазовые траектории САР второго порядка

Рассмотрим возможные случаи решения уравнения (1) и соответствующие им фазовые траектории.

1) , т.е.  - система в этом случае находится на границе устойчивости. Построим фазовые траектории, используя метод изоклин, т.е. уравнение (6) примет вид:

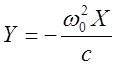
Задаёмся различными значениями константы «с» и строим изоклины, нанося на них чёрточки, означающие наклон касательных (Рис. 4)

·   - уравнение изоклины

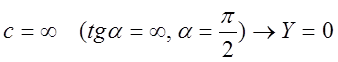·   - уравнение изоклины

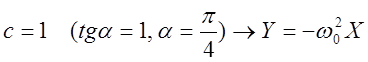·   - уравнение изоклины

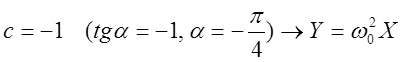·  , где  - уравнение изоклины

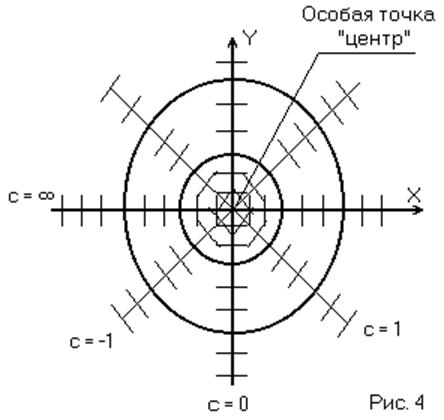
Судя по изоклинам, фазовые траектории в этом случае представляют из себя семейство эллипсов, вложенных друг в друга. Убедимся в этом. Решим уравнение (4) для случая

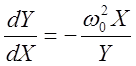             (8)

Для решения уравнения (8) перепишем его в виде             (9) и проинтегрируем:

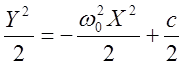     (10)

где «с» - постоянная интегрирования, определяется из начальных условий:

Подставим значения «с» в решение (10) и запишем:

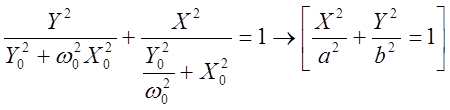 или         (11)

Уравнение (11) является уравнением эллипса с полуосями:

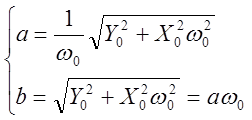
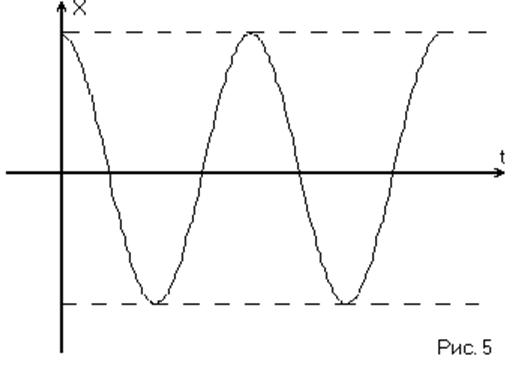
Изменяя начальные условия, будем получать семейство вложенных друг в друга концентрических эллипсов с центром в начале координат. При движении изображающей точки по фазовой траектории Х меняется от  до  и обратно, т.е. в САР в этом случае, как и следовало ожидать, возникают незатухающие колебания. (Рис. 5)

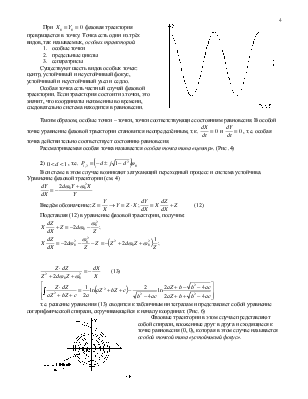
При  фазовая траектория превращается в точку. Точка есть один из трёх видов, так называемых, особых траекторий:

1.  особые точки

2.  предельные циклы

3.  сепаратрисы

Существуют шесть видов особых точек: центр, устойчивый и неустойчивый фокус, устойчивый и неустойчивый узел и седло.

Особая точка есть частный случай фазовой траектории. Если траектория состоит из точки, это значит, что координаты неизменны во времени, следовательно система находится в равновесии.

Таким образом, особые точки – точки, точки соответствующие состояниям равновесия. В особой точке уравнение фазовой траектории становится неопределённым, т.к. 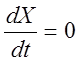 и 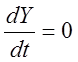, т.е. особая точка действительно соответствует состоянию равновесия.

Рассматриваемая особая точка называется особая точка типа «центр». (Рис .4)

2) , т.е.

В системе в этом случае возникают затухающий переходный процесс и система устойчива. Уравнение фазовой траектории (см. 4)

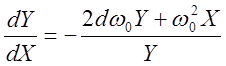
Введём обозначение: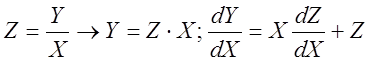            (12)

Подставляя (12) в уравнение фазовой траектории, получим:

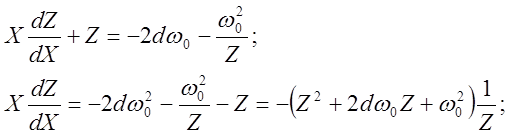
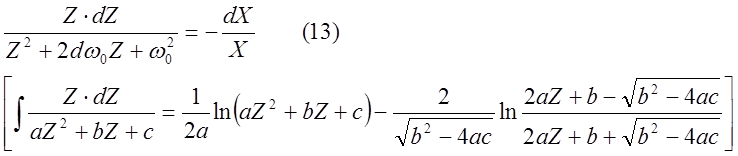
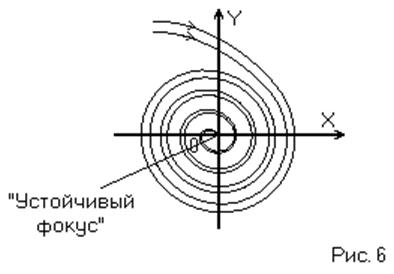т.е. решение уравнения (13) сводится к табличным интегралам и представляет собой уравнение логарифмической спирали, скручивающейся к началу координат. (Рис. 6)

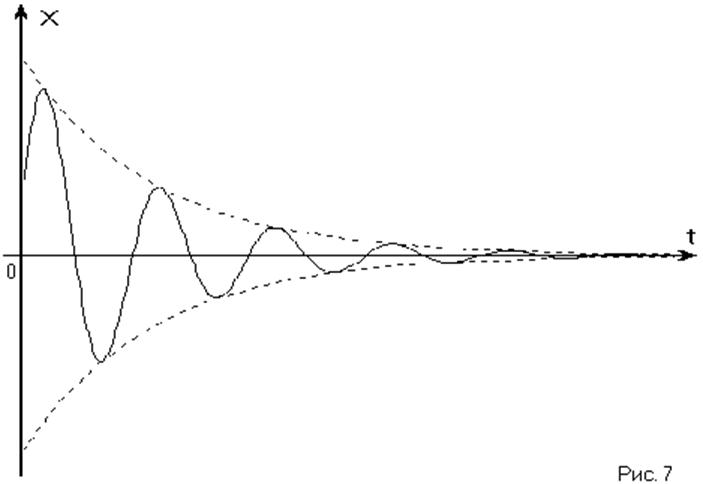
Фазовые траектории в этом случае представляют собой спирали, вложенные друг в друга и сходящиеся к точке равновесия (0, 0), которая в этом случае называется особой точкой типа «устойчивый фокус».

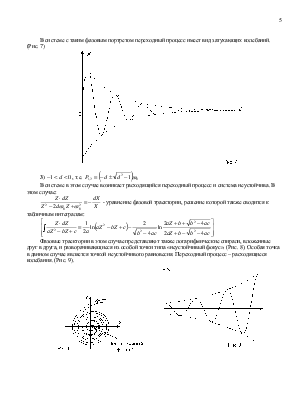
В системе с таким фазовым портретом переходный процесс имеет вид затухающих колебаний. (Рис. 7)

3) , т.е.

В системе в этом случае возникает расходящийся переходный процесс и система неустойчива. В этом случае:

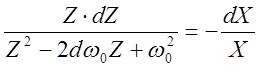 - уравнение фазовой траектории, решение которой также сводится к табличным интегралам:

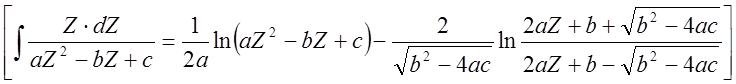
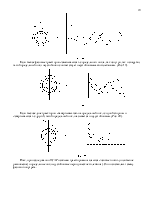
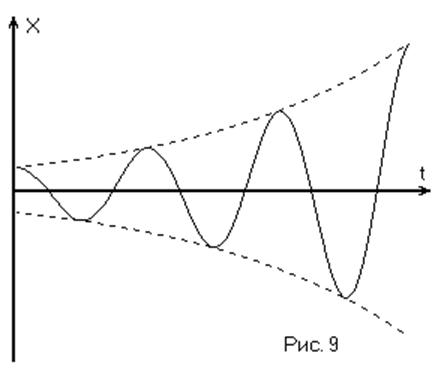
Фазовые траектории в этом случае представляют также логарифмические спирали, вложенные друг в друга, и разворачивающиеся из особой точки типа «неустойчивый фокус». (Рис. 8). Особая точка в данном случае является точкой неустойчивого равновесия. Переходный процесс – расходящиеся колебания. (Рис. 9).

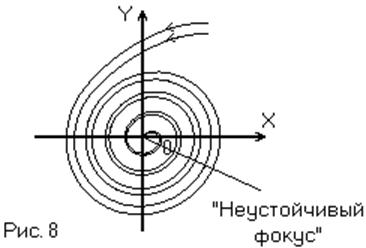
4) , т.е. корни характеристического уравнения – отрицательные, действительные, система устойчива, и в ней возникает апериодический переходный процесс. Выражение для фазовых траекторий находится также из уравнения (4) при использовании метода изоклин.

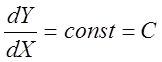, тогда  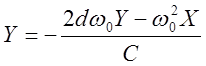и

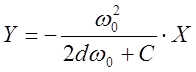            - уравнение изоклины

Фазовая траектория проходит под углом , следовательно уравнение фазовой траектории          

Решая совместно  и , находим

 и , где .

Следовательно,  - уравнение изоклин, которые одновременно являются фазовыми траекториями.

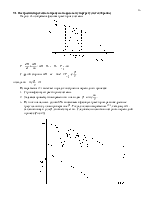
Особенность данного случая в том, что две изоклины одновременно являются и фазовыми траекториями AB и CD. (Рис. 10).

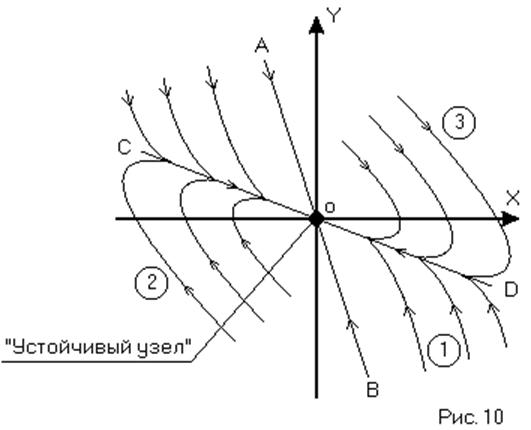
Система устойчива, фазовые траектории сходятся в особую точку типа «устойчивый узел». Изоклина AB полностью совпадает с одной из траекторий, изоклина CD является предельной траекторией, к которой стремятся все остальные.

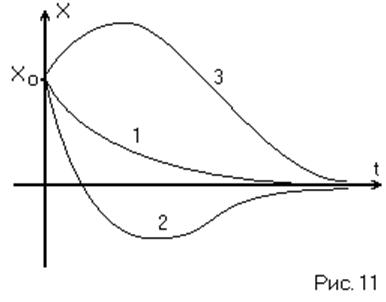
Внутри угла AOC (BOD) [обл. 1] значения X монотонно уменьшаются, т.е. переходный процесс апериодический. Вне этого угла [обл. 1, 2, 3] имеем область таких начальных значений, при которых переходный процесс имеет одно перерегулирование. (Рис. 11)