Методы расчета оптимальных значений параметров

Лекция №12

МЕТОДЫ РАСЧЕТА ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ

В инженерной практике часто ставится задача определения оптимальных значений параметров системы, структура и дифференциальные уравнения которой заданы. Такая задача обычно решается при расчете параметров оптимальной настройки регуляторов. При этом могут быть использованы уравнения Эйлера–Лагранжа (или Эйлера-Пуассона), уравнения Риккати, а также частотные методы и др.

Математически задачу определения параметров оптимальной настройки системы можно сформулировать следующим образом: заданы дифференциальные уравнения состояния системы

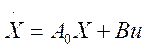;                    ,               (3.186)

где ; ; – матрица, элементы которой зависят от искомых параметров настройки системы (– коэффициенты уравнения объекта); X, u– векторы координат состояния и управлений;

требуется определить оптимальные значения параметров системы из условия экстремума выбранного критерия качества.

В ряде практических задач коэффициенты и  заданы и требуется определить коэффициенты .

Если рассматривается критерий качества в виде интеграла с квадратичной подинтегральной функцией 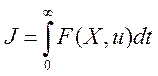, то для определения искомых  можно использовать уравнения вариационной задачи или уравнение Риккати. В тех случаях, когда рассматривается крите­рий качества в виде функции нескольких переменных (представляю­щих собой искомые параметры): , для определения можно использовать методы поиска экстремума функции несколь­ких переменных и частотные методы.

Расчет по уравнениям вариационной задачи. Известно, что для линейных одномерных объектов, динамика которых описывается ли­нейным дифференциальным уравнением вида

(3.187)

при квадратичном функционале критерия качества

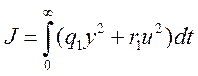                                                      (3.188)

оптимальное управление, доставляющее минимум интегралу (3.188), является линейной функцией координат состояния [7], поэтому

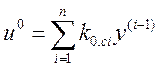                                                            3.189)

где – коэффициенты обратных связей регулятора.

Если равенство (3.189) подставить в (3.187), то получим уравне­ние объекта, выраженное через координаты объекта и параметры ре­гулятора :

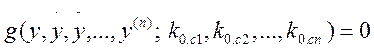.                                                                                                                    (3.190)

На основании (3.190) запишем характеристический полином системы F (р), и найдем сопряженный полином F(-р) после чего составим уравнение

F° (р) = F(p)F(-р).                                                 (3.191)

На основании (3.187) и (3.188) запишем функцию Лагранжа

(3.191)

и уравнения вариационной задачи: уравнения Эйлера – Пуассона типа (3.61) для у и  и  уравнения (3.187). Из уравнений вариационной задачи получим уравнение

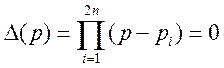                     ,                                       (3.193)

где П – знак произведения, подобное уравнению (3.191).

Приравнивая коэффициенты при одинаковых степенях р в урав­нениях для F°(p) и  , получим алгебраические уравнения отно­сительно неизвестных коэффициентов . Решение их позволяет найти искомые оптимальные параметры регулятора .

Расчет по уравнениям Риккати. Матрицу оптимальных парамет­ров регулятора . с можно определить по заданным уравнениям со­стояния (3.186) с использованием матричного уравнения Риккати, основываясь на методе принципа максимума. Для линейных объектов уравнение (3.114) можно записать в виде (3.186), а минимизируемый квадратичный функционал в общем случае представить в виде

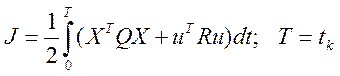                                   (3.194)о

где  и – матрицы, элементы которых  и .

Известно, что вектор координат оптимальных управлений, достав­ляющих минимум интегралу (3.194), является линейной функцией координат состояния [см. (3.186)].

Функция Гамильтона, определяемая выражением (3.121), в данном случае при  будет иметь вид

                       (3.195)

 При оптимальном управлении

,                                          

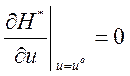или

,                            

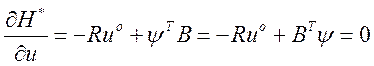откуда оптимальное управление

.                                           (3.196)

Управление (3.196) обеспечивает максимум гамильтониана (3.195), так как при положительно определенной матрице R

,

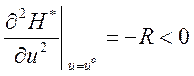Используя (3.195) и (3.196), запишем канонические уравнения:

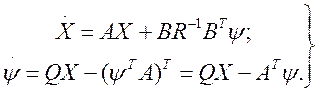                                      (3.197)         

Для определения оптимального управления (3.196) необходимо из уравнений (3.197) найти вектор вспомогательных функций W(см. § 3.6).

Однако в данном случае можно не производить интегрирование уравнений (3.197), а использовать уравнение Риккати, что позволяет упростить решение задачи.

Рассмотрим способ получения уравнения Риккати. В общем случае можно записать уравнение

                                            (3.198)

дифференцируя которое, найдем

                                                   (3.199)

где  – матрица неизвестных коэффициентов размерности (пхп):

Подставив (3.198) в уравнения системы (3.197), получим:

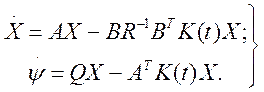                                   (3.200)        

Если подставить в (3.199) вместо  первое уравнение системы (3.200), то запишем

                    (3.201)

Приравнивая правые части уравнения (3.201) и второго уравнения (3.200), получим матричное дифференциальное уравнение

                (3.202)

называемое уравнением Риккати. Решение уравнения (3.202) опреде­ляет матрицу , подставляя которую в (3.    198) и учитывая (3.196), получим выражение для оптимального управления

(3.203)

Для полностью управляемых объектов с постоянными во времени параметрами при [см. (3.194)]  и , поэтому оптимальное управление принимает форму

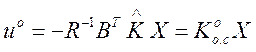,                                        (3.204)

откуда

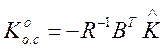,                                                (3.205)

где – положительно определенная симметричная матрица размер­ности (пxп), состоящая из постоянных коэффициентов  (при ), определяемая уравнением (3.202) с учетом  и :

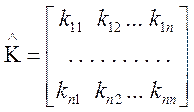                                              (3.206)

Оптимальное управление (3.204) минимизирует квадратичный функционал (3.194) для объектов с постоянными параметрами и . Таким образом, для определения оптимальных парамет­ров регулятора необходимо найти матрицу  и подставить в (3.205). Для объектов с переменными параметрами, а также с постоянными параметрами при конечной величине  необходимо определять матрицу К(t). Основная трудность решения такой задачи состоит в том, что уравнение (3.202) является нелинейным дифференциальным матричным уравнением, для интегрирования которого требуется при­менение вычислительных машин. В этом случае регулятор будет иметь переменные параметры, т. е. .