Саратовский государственный технический университет.
Кафедр СИИ.
Лабораторная работа №1.
Тема: МОДЕЛИРОВАНИЕ УСИЛИТЕЛЬНЫХ, ИНТЕГРИРУЮЩИХ И ДИФФЕРЕНЦИРУЮЩИХ
ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.
Вариант 10
Выполнила:
Проверил:
Саратов
2009
ЦЕЛЬ РАБОТЫ: Расчетно-экспериментальное исследование временных и частотных характеристик усилительного, интегрирующего и дифференцирующего звеньев, приобретение практических навыков их математического моделирования с использованием программы MatLab Simulink.
Исходные данные
к=3.2e-1
Переходный процесс интегратора-сумматора.
Аналитический расчет:
Переходная функция интегрирующего звена определяется выражением:
|
|
Где l(t)-бесконечная ступенька, т.е 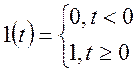 .
.
Составим таблицу значенийаналитически:
|
t |
k |
h(t) |
|
1 |
3,20E-03 |
3,20E-03 |
|
100 |
3,20E-03 |
3,20E-01 |
|
200 |
3,20E-03 |
6,40E-01 |
|
300 |
3,20E-03 |
9,60E-01 |
|
400 |
3,20E-03 |
1,28 |
|
500 |
3,20E-03 |
1,60 |
|
600 |
3,20E-03 |
1,92 |
|
700 |
3,20E-03 |
2,24 |
|
800 |
3,20E-03 |
2,56 |
|
900 |
3,20E-03 |
2,88 |
|
1000 |
3,20E-03 |
3,20 |
Код программы для аналитического расчета:
>> t=[1 100 200 300 400 500 600 700 800 900 1000];
>> h_t=[3.2e-3 3.2e-1 6.4e-1 9.6e-1 1.28 1.6 1.92 2.24 2.56 2.88 3.2];
>> plot(t,h_t)
xlabel( ' t ' )
ylabel( ' h(t) ' )
title( ' График переходного процесса ' );
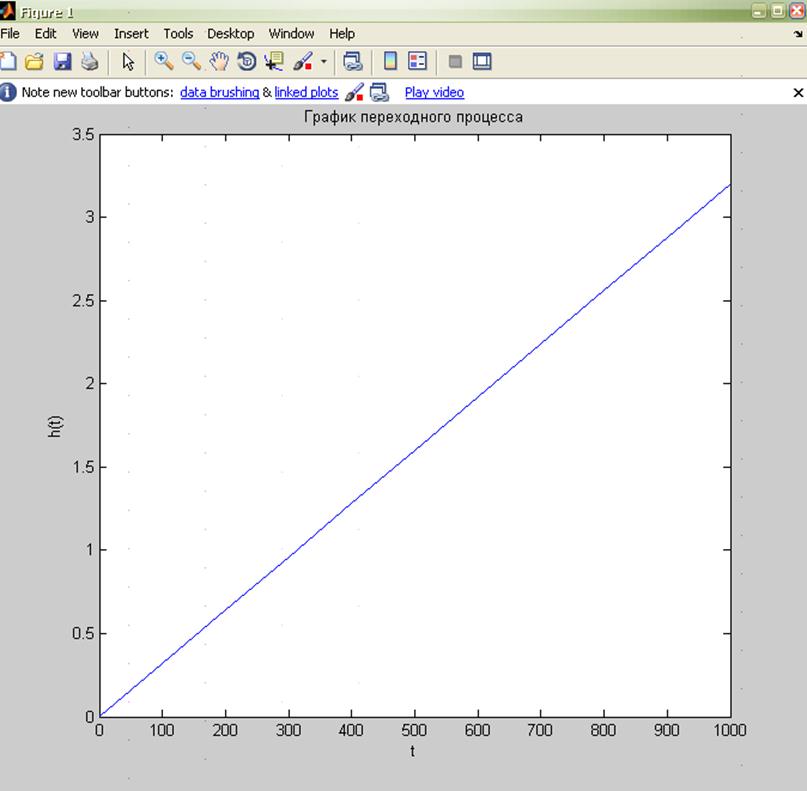
Построим график переходного процесса в пакете
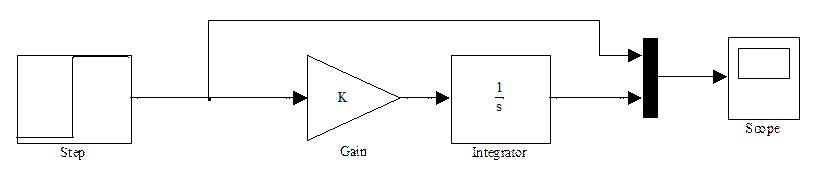
Соберём схему в пакете Simulink :
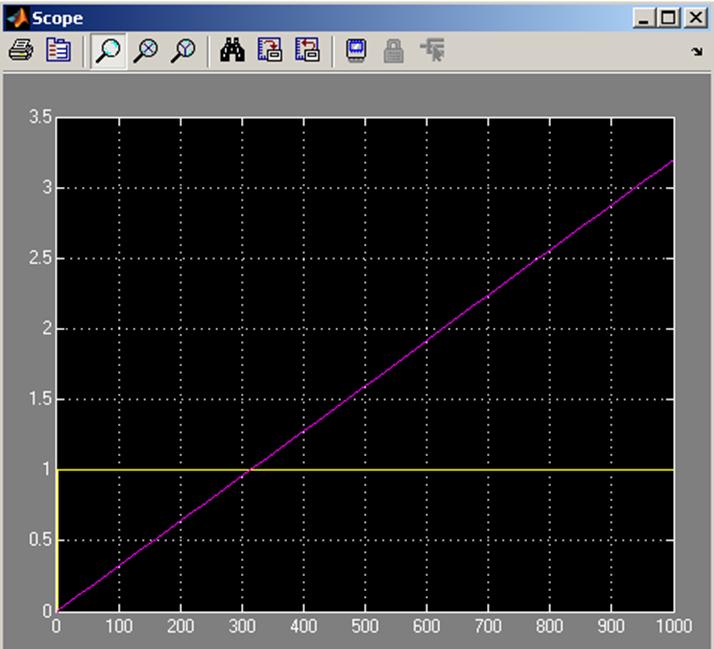
Составим таблицу значений полученных из графика:
|
t |
h(t) |
|
100 200 300 400 500 600 700 800 900 1000 |
0,3 0,64 0,95 1,27 1,6 1,93 2,24 2,56 2,85 3,2 |
Из данной таблицы видно, что полученная модель достаточно точно описывает переходный процесс, получаемый при аналитическом расчете.
Интегрирующее звено.
Аналитический расчет.
Амплитудно-частотная характеристика.
Расчет проводим по формуле:
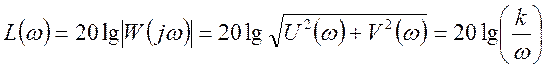
Получаем таблицу значений амплитудно-частотной характеристики:
|
ω |
k |
log(ω) |
L2(ω) |
|
k/5=5,33E-04 |
3,20E-03 |
-3,273001272 |
1,56E+01 |
|
k/4=6,40E-04 |
3,20E-03 |
-3,193820026 |
1,40E+01 |
|
k/3=8,00E-04 |
3,20E-03 |
-3,096910013 |
1,20E+01 |
|
k/2=1,07E-03 |
3,20E-03 |
-2,971971276 |
9,54 |
|
k/1=1,60E-03 |
3,20E-03 |
-2,795880017 |
6,02 |
|
k=3,20E-03 |
3,20E-03 |
-2,494850022 |
0 |
|
2*k=6,40E-03 |
3,20E-03 |
-2,193820026 |
-6,02 |
|
3*k =9,60E-03 |
3,20E-03 |
-2,017728767 |
-9,54 |
|
4*k =1,28E-02 |
3,20E-03 |
-1,89279003 |
-1,20E+01 |
|
5*k =1,60E-02 |
3,20E-03 |
-1,795880017 |
-1,40E+01 |
|
6*k =1,92E-02 |
3,20E-03 |
-1,716698771 |
-1,56E+01 |
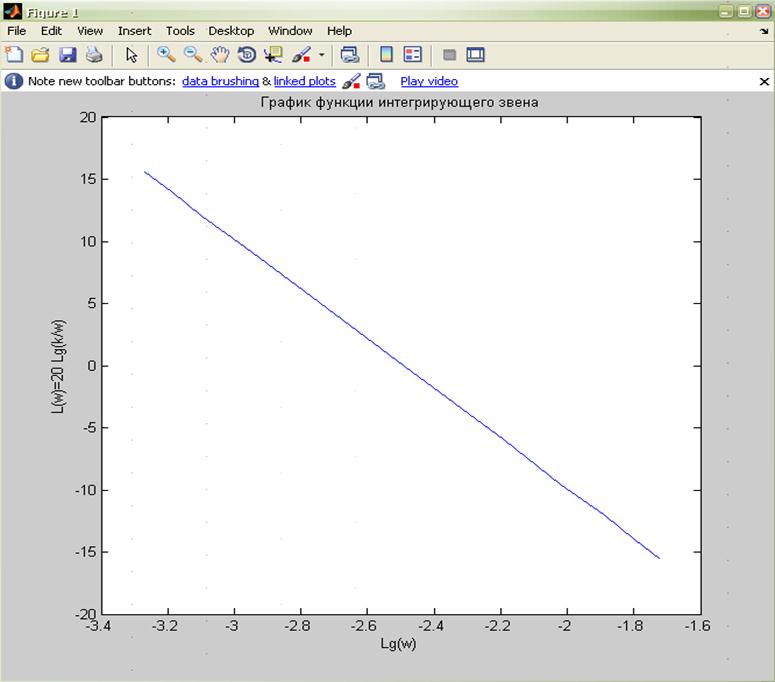
Код программы для аналитического расчета:
>> Lg_w=[-3.27 -3.19 -3.097 -2.97 -2.79 -2.49 -2.19 -2.02 -1.89 -1.796 -1.72];
>> L=[15.6 14 12 9.54 6.02 0 -6.02 -9.54 -12 -14 -15.6];
>> plot(Lg_w,L)
xlabel( ' Lg(w) ' )
ylabel( ' L(w)=20 Lg(k/w) ' )
title( ' График функции интегрирующего звена ' );
По таблице строим график:
Фазово-частотная характеристика:
Расчет проводим по формуле:
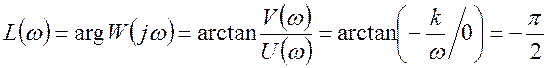
Из
формулы видно что при любом ![]() L(
L(![]() )
будет равна -pi/2 и ФЧХ будет иметь вид:
)
будет равна -pi/2 и ФЧХ будет иметь вид:

Экспериментальный расчет.
Используя схему из Simulink’a.
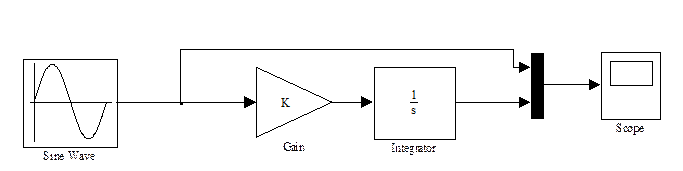
Получим:
Составим таблицу значений:
|
ω |
k |
log(ω) |
W(j ω) |
L(ω)=20log(W(j ω)) |
|
|
k/5=5,33E-04 |
3,20E-03 |
-3,273001272 |
6 |
15,56303 |
|
|
k/4=6,40E-04 |
3,20E-03 |
-3,193820026 |
5 |
13,9794 |
|
|
k/3=8,00E-04 |
3,20E-03 |
-3,096910013 |
4 |
12,0412 |
|
|
k/2=1,07E-03 |
3,20E-03 |
-2,971971276 |
3 |
9,542425 |
|
|
k/1=1,60E-03 |
3,20E-03 |
-2,795880017 |
2 |
6,0206 |
|
|
k=3,20E-03 |
3,20E-03 |
-2,494850022 |
1 |
0 |
|
|
2*k=6,40E-03 |
3,20E-03 |
-2,193820026 |
5,00E-01 |
-6,0206 |
|
|
3*k =9,60E-03 |
3,20E-03 |
-2,017728767 |
3,30E-01 |
-9,62972 |
|
|
4*k =1,28E-02 |
3,20E-03 |
-1,89279003 |
2,50E-01 |
-12,0412 |
|
|
5*k =1,60E-02 |
3,20E-03 |
-1,795880017 |
2,00E-01 |
-13,9794 |
|
|
6*k =1,92E-02 |
3,20E-03 |
-1,716698771 |
1,64E-01 |
-15,7031 |
|
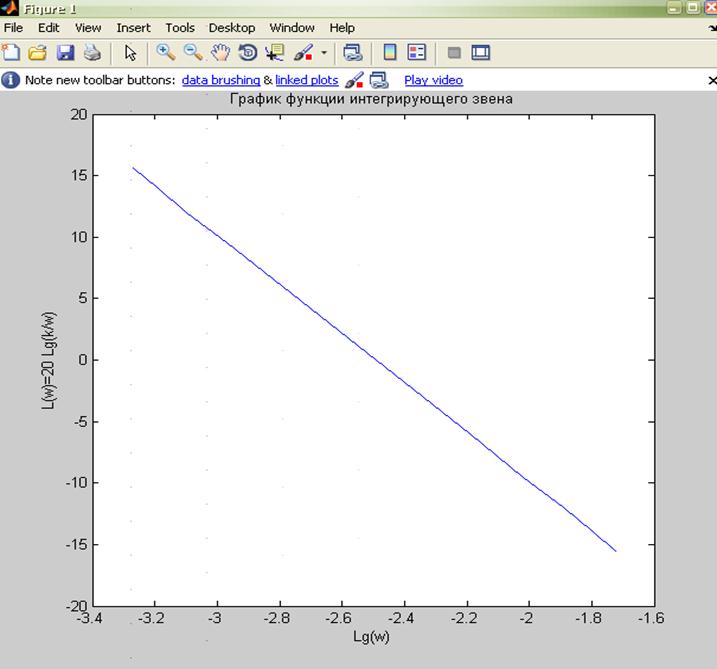
Код программы для практического расчета:
>> Lg_w=[-3.27 -3.19 -3.097 -2.97 -2.79 -2.49 -2.19 -2.02 -1.89 -1.796 -1.72];
>> L=[15.56 13.98 12.04 9.54 6.02 0 -6.02 -9.63 -12.04 -13.98 -15.7];
>> plot(Lg_w,L)
xlabel( ' Lg(w) ' )
ylabel( ' L(w)=20 Lg(k/w) ' )
title( ' График функции интегрирующего звена ' );
По данным таблицы строим график.
Получим таблицу для фазово-частотной характеристики:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.