Другие предметы \ Теория автоматического управления

Моделирование усилительных, интегрирующих и дифференцирующих звеньев систем автоматического управления, страница 2

ω

k

log(ω)

T1

T

φ(ω )

k/5=5,33E-04

3,20E-03

-3,273001272

3000

12000,00

-0,5

k/4=6,40E-04

3,20E-03

-3,193820026

2500

10000,00

-0,5

k/3=8,00E-04

3,20E-03

-3,096910013

2000

8000

-0,5

k/2=1,07E-03

3,20E-03

-2,971971276

1500

6000,00

-0,5

k/1=1,60E-03

3,20E-03

-2,795880017

1000

3900,00

-0,512821

k=3,20E-03

3,20E-03

-2,494850022

500

1940,00

-0,515464

2*k=6,40E-03

3,20E-03

-2,193820026

250

990,00

-0,505051

3*k =9,60E-03

3,20E-03

-2,017728767

1,75E+02

7,20E+02

-0,486111

4*k =1,28E-02

3,20E-03

-1,89279003

1,25E+02

5,00E+02

-0,5

5*k =1,60E-02

3,20E-03

-1,795880017

1,00E+02

3,80E+02

-0,526316

6*k =1,92E-02

3,20E-03

-1,716698771

8,00E+01

3,25E+02

-0,492308

По данным таблицы строим график:

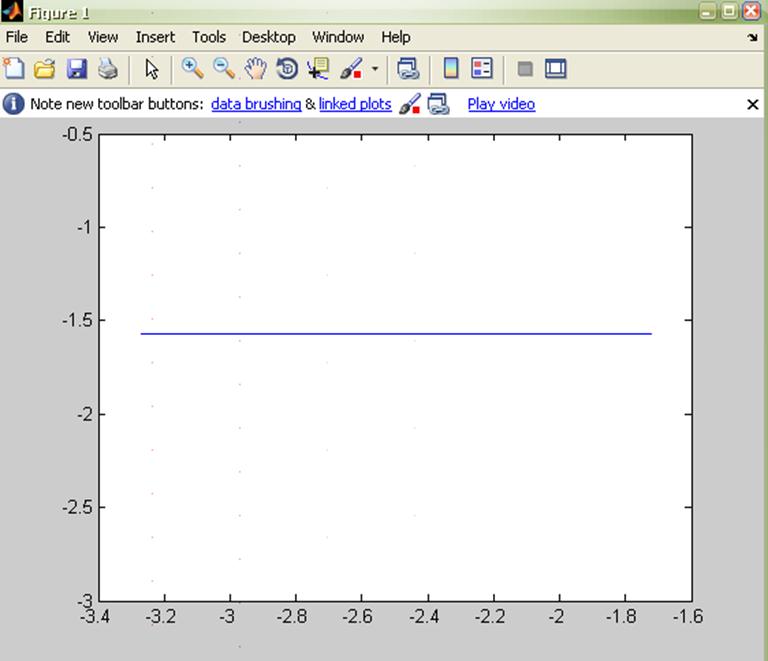
Дифференцирующее звено.

Аналитический расчет.

Амплитудно-частотная характеристика.

Вычисления проводим по формуле:

Получаем таблицу значений для амплитудно-частотной характеристики.

ω

k

log(ω)

L1(ω)

1/(6*k)=5,21E+01

3,20E-03

1,71669877

-15,563

1/(5*k)=6,25E+01

3,20E-03

1,79588002

-13,9794

1/(4*k)=7,81E+01

3,20E-03

1,89279003

-12,0412

1/(3*k)=1,04E+02

3,20E-03

2,01772877

-9,54243

1/(1*k)=1,56E+02

3,20E-03

2,19382003

-6,0206

1/k=3,13E+02

3,20E-03

2,49485002

0

2/k=6,25E+02

3,20E-03

2,79588002

6,0206

3/k=9,38E+02

3,20E-03

2,97197128

9,542425

4/k=1,25E+03

3,20E-03

3,09691001

12,0412

5/k=1,56E+03

3,20E-03

3,19382003

13,9794

6/k=1,88E+03

3,20E-03

3,27300127

15,56303

Код программы для аналитического расчета:

>> Lg_w=[1.72  1.79  1.89 2.02 2.19 2.49 2.79 2.97 3.1 3.19 3.27];

>> L=[-15.563  -13.979  -12.04  -9.54  -6.02 0  6.02  9.54  12.04  13.979  15.563];

>> plot(Lg_w,L)

xlabel( ' Lg(w) ' )

ylabel( ' L(w)=20 Lg(k*w) ' )

title( ' График функции дифференцирующего звена ' );

По данным таблицы строим график.

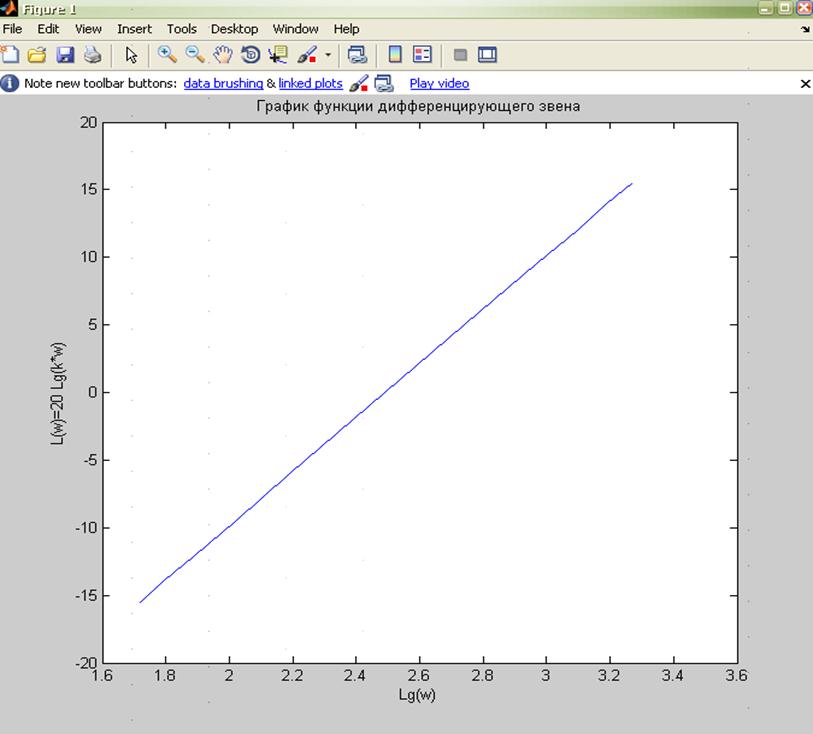
Фазово-частотная характеристика:

Вычисление значений для фазово-частотной характеристики выполняем по формуле:

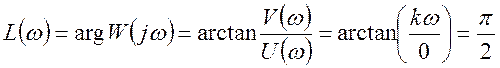
Получаем таблицу значений для фазово-частотной характеристики.

ω

log(ω)

φ(ω )

1/(6*k)=5,21E+01

1,71669877

0.5pi

1/(5*k)=6,25E+01

1,79588002

0.5pi

1/(4*k)=7,81E+01

1,89279003

0.5pi

1/(3*k)=1,04E+02

2,01772877

0.5pi

1/(1*k)=1,56E+02

2,19382003

0.5pi

1/k=3,13E+02

2,49485002

0.5pi

2/k=6,25E+02

2,79588002

0.5pi

3/k=9,38E+02

2,97197128

0.5pi

4/k=1,25E+03

3,09691001

0.5pi

5/k=1,56E+03

3,19382003

0.5pi

6/k=1,88E+03

3,27300127

0.5pi

По данным таблицы строим график:

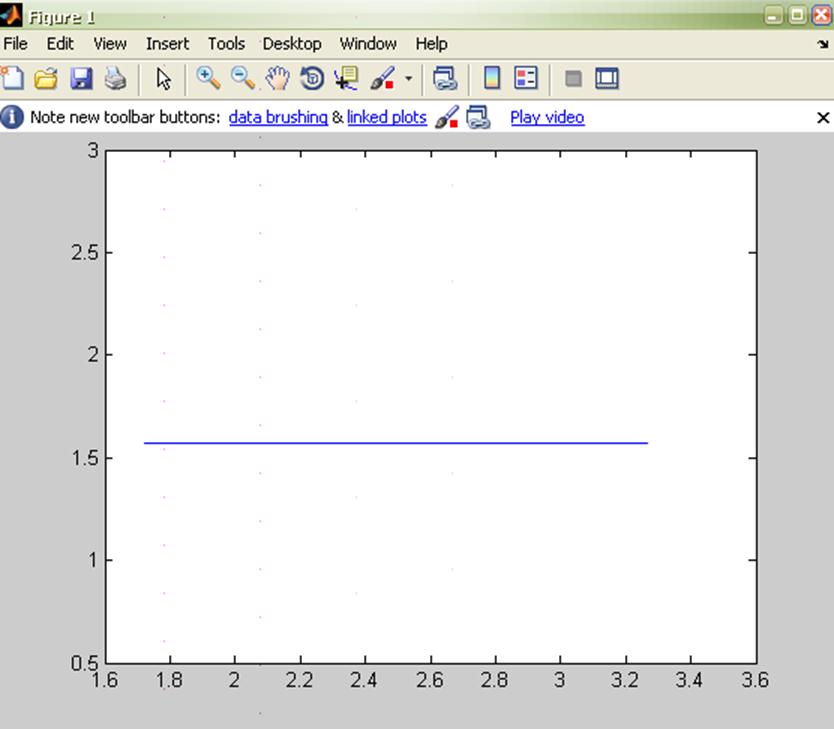
Практический расчет.

Используя схему из Simulinka

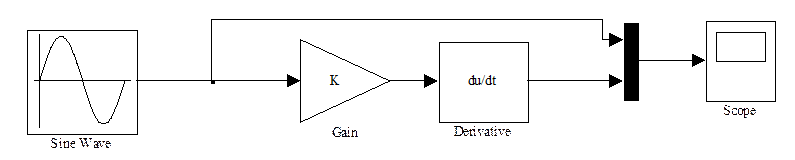
Получим:

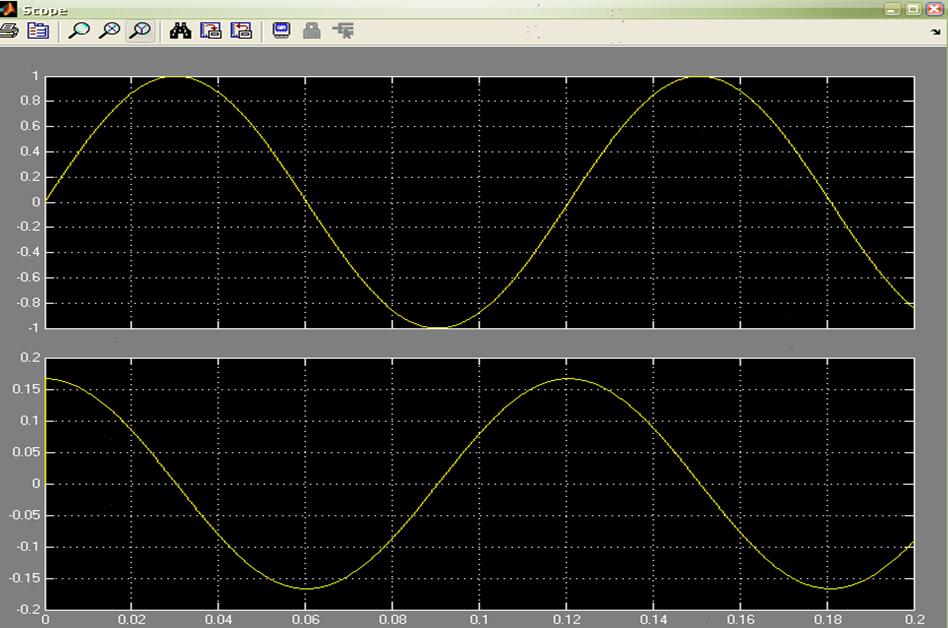
Составим таблицу значений:

ω

k

log(ω)

W(j ω)

L(ω)=20log(W(j ω))

1/(6*k)=5,21E+01

3,20E-03

1,71669877

0,166

-15,5978

1/(5*k)=6,25E+01

3,20E-03

1,79588002

0,2

-13,9794

1/(4*k)=7,81E+01

3,20E-03

1,89279003

0,25

-12,0412

1/(3*k)=1,04E+02

3,20E-03

2,01772877

0,333

-9,55112

1/(1*k)=1,56E+02

3,20E-03

2,19382003

0,5

-6,0206

1/k=3,13E+02

3,20E-03

2,49485002

1

0

2/k=6,25E+02

3,20E-03

2,79588002

2

6,0206

3/k=9,38E+02

3,20E-03

2,97197128

3

9,542425

4/k=1,25E+03

3,20E-03

3,09691001

4

12,0412

5/k=1,56E+03

3,20E-03

3,19382003

5

13,9794

6/k=1,88E+03

3,20E-03

3,27300127

6

15,56303

Код программы для практического расчета:

         >> Lg_w=[1.72 1.79 1.89 2.02 2.19 2.49 2.79 2.97 3.1 3.19 3.27];

>> L=[-15.563 -13.979 -12.04 -9.54 -6.02 0 6.02 9.54 12.04 13.979 15.563];

>> plot(Lg_w,L)

xlabel( ' Lg(w) ' )

ylabel( ' L(w)=20 Lg(k*w) ' )

title( ' График функции дифференцирующего звена ' );

По данным таблицы строим график. 

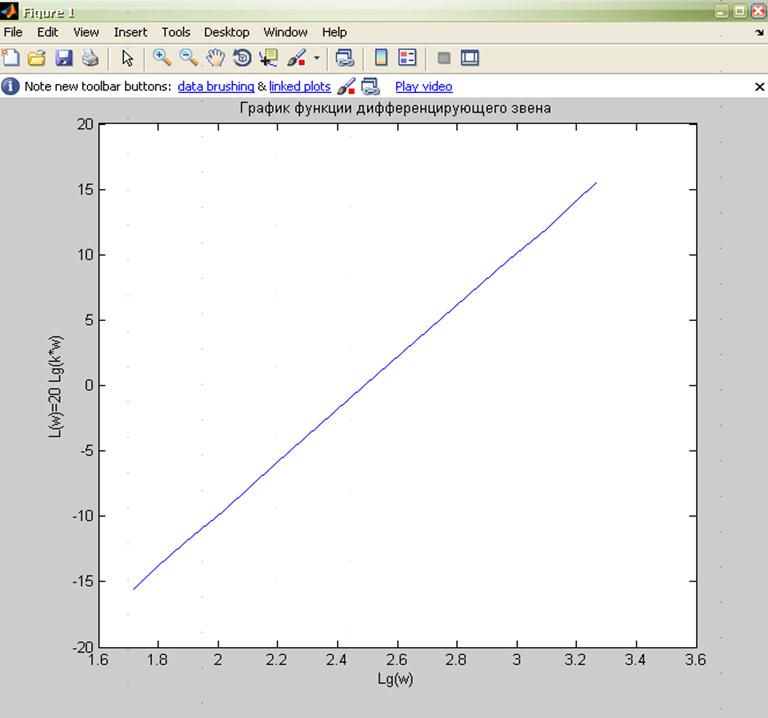
Фазово-частотная характеристика:

ω

log(ω)

T1

T

φ(ω )

1/(6*k)=5,21E+01

1,71669877

0,03

0,12

0,5

1/(5*k)=6,25E+01

1,79588002

0,025

0,09

0,555556

1/(4*k)=7,81E+01

1,89279003

0,02

0,08

0,5

1/(3*k)=1,04E+02

2,01772877

0,016

0,06

0,533333

1/(1*k)=1,56E+02

2,19382003

0,01

0,04

0,5

1/k=3,13E+02

2,49485002

0,005

0,02

0,5

2/k=6,25E+02

2,79588002

2,50E-03

1,00E-02

0,5

3/k=9,38E+02

2,97197128

1,70E-03

6,90E-03

0,492754

4/k=1,25E+03

3,09691001

1,30E-03

5,00E-03

0,52

5/k=1,56E+03

3,19382003

1,00E-03

4,00E-03

0,5

6/k=1,88E+03

3,27300127

8,00E-04

3,30E-03

0,484848

По данным таблицы строим график. 

Оценка погрешности.

 Погрешность не превышает 2% для всех вычислений, что подтверждает высокую точность и правильность выполнения задания. В связи с этим не приведены совмещенные графики аналитического и экспериментального расчетов, так как из-за маленькой погрешности они сливаются.

Вывод.

В ходе работы мы провели расчетно-экспериментальное исследование временных и частотных характеристик усилительного, интегрирующего и дифференцирующего звеньев, приобрели практические навыки в математическом моделировании с использованием MatLab Simulink и убедились в высокой точности и наглядности данного программного пакета.

Скачать файл