Наблюдение детерминированных объектов

3.Наблюдение детерминированных объектов.

В предыдущем разделе было показано, что если все переменные состояния объекта представляют собой измеримые физические величины, то синтез замкнутой системы с заданным распределением полюсов не представляет какой-либо трудности. Однако в большинстве случаев доступны приборному измерению лишь некоторые переменные состояния. Кроме того, использование измерительных приборов не всегда желательно. Некоторые измерительные устройства описываются сложными уравнениями, существенно изменяющими структуру объекта управления. Решение задачи управления по неполной обратной связи может не дать требуемого качества. Эти обстоятельства указывают на необходимость способов, которые косвенно позволили бы оценить переменные состояния, мало доступные или вовсе недоступные прямому измерению. Такие способы основаны на использовании уравнений движения объекта. Эти уравнения предполагаются известными. Устройства для определения координат состояния объекта, в основу которых положены уравнения его движения называются наблюдающими устройствами.  

                       Оглавление

3.1. Наблюдающееустройство как замкнутая система…….1

3.2. Общая теория наблюдающих устройств……………….3

3.3. Наблюдающее устройство идентификации……………4

3.4. Разделение собственных значений……………………..5

3.5. Редуцированное наблюдающее устройство……………7

3.1. Наблюдающее устройство как замкнутая система.

Предположим, что уравнения объекта имеют вид

                                                                (3.1)

Доступный измерению скалярный выходной сигнал

                               ,                                                  (3.2)

                                 

Доступный измерению  матричный  входной  сигнал обозначим как   Размеры матриц соответственно равны:

                                 

                             

Опираясь на знание сигналов   и матриц A и B необходимо оценить вектор состояния объекта X(t).

Обозначим оценочное значение вектора состояния как  Тогда оценочное значение выходного сигнала будет  Оценка содержит ошибку, если   отличается от результата, полученного реальным измерением  сигнала y.  Задача состоит в том, чтобы ошибку 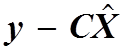  свести к нулю.

Зная A,B,U(t) и начальное значение вектора состояния, можно оценить координаты состояния, если подвести сигнал U(t) к электронной модели объекта

                                                             (3.3)

Cхема  модели может быть изображена следующим образом  (рис.3.1).

                             

                                           +                                   

                                                                                               

           Рис.3.1. Схема электронной модели системы.

Недостаток оценивающего устройства (3.3) состоит в том, что оно работает по разомкнутому циклу и, поскольку данные об A,B и U(t)  неточны, после некоторого времени работы это устройство будет давать слишком неточную оценку вектора состояния. Чтобы при сохранении линейности данного устройства устранить отмеченный недостаток , введем ошибку 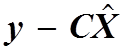  в каждое из уравнений системы (3.3)

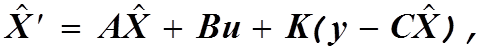                                  (3.4)

где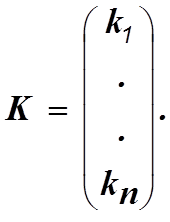                   

Схема наблюдающего устройства примет вид

                                X                        Y                                          U

U        Объект                     С                +            С              Модель

                                                                                                        

 

             Рис.3.2.Схема наблюдающего устройства.

Устройство, описываемое уравнением (3.4) оценивает вектор состояния по замкнутому циклу и, в дальнейшем, называется наблюдающим. Определим ошибку оценивания как

                                                                             (3.5)

и вычтем уравнение (3.1) из уравнения (3.4)

      

                        (3.6)

Выбрав коэффициенты    так, чтобы  система (3.6) была устойчивой, получим, что     при   Другими словами, с ростом времени t оценка   стремится к оцениваемому вектору X(t).

3.2.Общая теория наблюдающих устройств.

Рассмотрим вначале задачу наблюдения свободного объекта , т.е. объекта входной сигнал которого равен нулю. Если  имеющиеся в распоряжении выходы этого объекта используются в качестве входов линейной системы  , то последняя почти всегда может служить в качестве наблюдающего устройства объекта    в том смысле, что ее состояние отслеживает линейное преобразование вектора состояния объекта.

                          X

                                                            Z

           Рис.3.3.Объект и наблюдающее устройство.

Пусть  свободный объект с уравнением

                                                                   (3.7)

воздействует на систему  ,которая описывается уравнением

      .                                           (3.8)  

Предположим, что существует матрица преобразования  Т, удовлетворяющая уравнению

                       .                                                (3.9)

Умножим слева уравнение (3.7) на Т и вычтем его из уравнения (3.8).

   
Подставив вместо  H выражение (9), прийдем  к уравнению

                              (3.10)
Обозначим:        Тогда из (3.10) следует, что

                

      
Если  то   и условие   выполняется для всех   В более общем случае, когда  получим

                            (3.11)
 При отрицательных собственных числах матрицы F 

Можно доказать, что уравнение (3.9) имеет единственное решение Т, если  у матриц A и F нет общих собственных значений. Таким образом некоторая система  корни которой отличны от корней объекта   может служить для этого объекта наблюдающим устройством в том смысле, что ее вектор состояния  Z(t) связан с вектором состояния объекта соотношением  Z=TX, где матрица Т, определяемая из уравнения (9) зависит от параметров систем   и  

Аналогично можно получить наблюдающее устройство и для случая возмущенного объекта, когда   Для этого нужно, чтобы сигнал U(t), подведенный к наблюдающему устройству поддавался измерению. В этом случае объект    описывается уравнением

                        ,

а наблюдающее устройство

                             (3.12)
Уравнение  (3.12) будет по-прежнему иметь решением выражение (3.11). Отсюда следует, что наблюдающее устройство для возмущенного объекта можно синтезировать, полагая вначале объект свободным, а затем добавляя входной сигнал, как это показано в (3.12).