Наблюдение детерминированных объектов, страница 2

        
            3.3. Наблюдающее устройство идентификации.

Это наблюдающее устройство характеризуется тем, что матрица преобразования Т, связывающая вектор состояния наблюдающего устройства с  вектором состояния наблюдаемого объекта единичная. Тогда Z(t)=TX(t)=IX(t)=X(t), т.е. наблюдающее устройство идентифицирует вектор состояния объекта. Требование T=I может быть выполнено выбором матриц F и H.

Подставив T=I в (3.9), получим F=A-H. Отсюда следует, что наблюдающее устройство и объект имеют один и тот же порядок. Матрица H определяется не только порядком измеряемого вектора выходных сигналов объекта, но и структурой входа наблюдающего устройства.

Если объект с r-мерным выходом Y(t)  описывается уравнениями

                                                                                  (3.13)

                  ,                                                                     

а наблюдающее устройство- уравнением

                                                      
то H=KC. При синтезе наблюдающего устройства  матрица С фиксирована, а   матрица К произвольна.  Следовательно наблюдающее устройство идентификации   однозначно определяется выбором матрицы К и в случае возмущенного объекта описывается уравнением

          

Cтруктурная схема этого наблюдающего устройства показана на рисунке 3.4.

                                                                                   Y

                      K                      

  U(t)          B        +        +                                  

                                                    A-KC

Рис.3.4.Наблюдающее устройство идентификации.

Собственные колебания наблюдающего устройства определяются собственными значениями матрицы  (А-КС). Следовательно матрицу К нужно выбирать так, чтобы обеспечить устойчивость наблюдающего устройства, в частном случае задать его корням требуемые значения. Последнее возможно, если система (13)  полностью наблюдаема.

3.4 Разделение собственных значений.

Докажем теперь, что корни замкнутой системы, образованной объектом, наблюдающим устройством идентификации, которое используется в качестве измерительного устройства переменных состояния, и регулятором, разбиваются на две независимые группы. Одна группа- это корни замкнутой системы "объект-регулятор", синтезированной в предположении непосредственного измерения всех переменных состояния объекта; другая группа- корни наблюдающего устройства, представляющего независимую динамическую систему. В данном случае уравнения всей системы будут

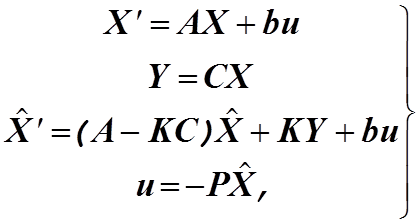                                       (3.14)

где первое и второе уравнения описывают объект с одним входом и одним выходом, а третье и четвертое уравнения- наблюдающее устройство идентификации и регулятор. Вводя вместо переменных переменны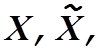е  где 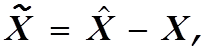уравнения (3.14) преобразуются к виду

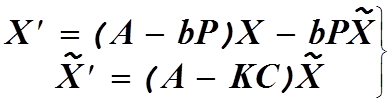                                                         (3.15)

Второе уравнение системы (3.15) получается вычитанием первого уравнения системы (3.14) из третьего и заменой  Y на CX. Первое уравнение системы (3.15) образуется подстановкой u=-PX в первое уравнение системы (3.14) и последующей заменой   

Система уравнений (15) имеет треугольную матрицу

         

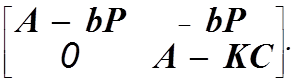
Отсюда следует, что характеристический полином этой системы

        

представляет собой произведение характеристического полинома замкнутой системы "объект-регулятор" и характеристического полинома наблюдающего устройства.

Таким образом, регулятор Р можно синтезировать, предполагая идеально точное непосредственное измерение переменных состояния объекта, а параметры наблюдающего устройства выбирать, руководствуясь только желаемыми динамическими свойствами этого устройства. Обычно матрица К выбирается такой, чтобы корни наблюдающего устройства были несколько более отрицательными, чем корни замкнутой системы, состоящей из объекта  и регулятора, формирующего по выходному сигналу наблюдающего устройства закон регулирования.

Пример. Рассмотрим объект, структурная схема которого показана на рис.3.5. Записывая согласно схеме дифференциальные уравнения отдельных звеньев, получим следующие уравнения объекта в переменных состояния:

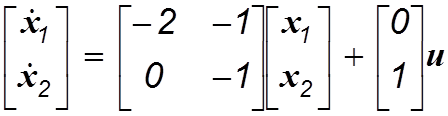                              (3.16)

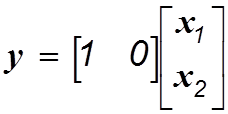        .                                                    (3.17)

                                                      

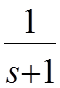
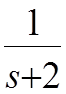
               Рис.3.5.Объект второго порядка.

Поскольку выход объекта  -скалярная величина, матрица К, характеризующая вход наблюдающего устройства идентификации, должна быть типа , т.е.

                 

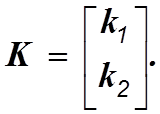
Тогда матрица этого наблюдающего устройства будет

  

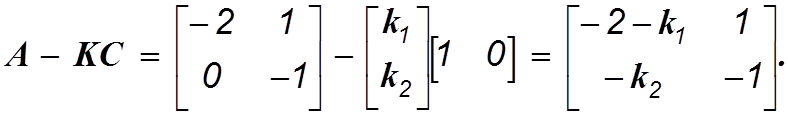
Характеристический полином наблюдающего устройства

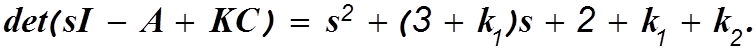        (3.18)

Предположим, что для наблюдающего устройства желателен двукратный корень -3. В этом случае желаемым характеристическим полиномом этого устройства будет

                                                   (3.19)

Приравнивая коэффициенты при одинаковых степенях s в уравнениях (3.18) и(3.19) получим: 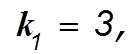 Следовательно, наблюдающее устройство идентификации описывается уравнением

    

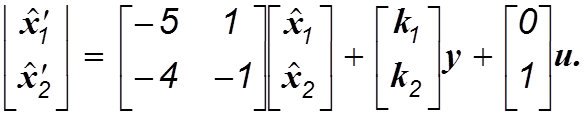
3.5 Редуцированное наблюдающее устройство.

Наблюдающее устройство идентификации обладает некоторой степенью избыточности. Эта избыточность выражается в том, что данное устройство оценивает весь вектор состояния объекта Х(t), хотя часть этого вектора можно  определить и по результатам непосредственного измерения выходного сигнала y. Избыточность можно устранить, синтезируя редуцированное наблюдающее устройство,т.е. устройство, порядок которого более низок, чем порядок наблюдаемого объекта.

Если вектор y(t) выходных сигналов объекта, поддающихся измерению, имеет размерность r , то для оценки всего n-мерного вектора состояния объекта x(t) достаточно синтезировать наблюдающее устройство порядка n-r, характеризуемое вектором состояния z(t)  размерности n-r.

Пусть Т-матрица типа  преобразующая вектор Х в вектор Z. Тогда оценку всего вектора состояния можно получить из уравнения

            

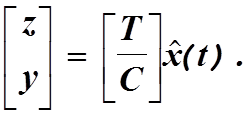
Решая это уравнение относительно оценки вектора состояния, получим

             

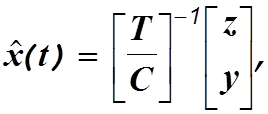
где в правой части находится измеряемый вектор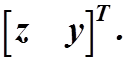 

Редуцированное наблюдающее устройство можно синтезировать следующим образом. Пусть объект описывается уравнениями

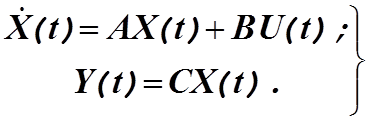           (3.20)

Без потери общности можно считать, что  r выходов объекта линейно независимы. Это эквивалентно тому, что матрица С имеет ранг r. Имеется возможность такой замены переменных, при которой матрицу С можно преобразовать к виду 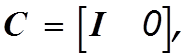  где I-единичная матрица типа   а О- матрица типа  все элементы которой равны нулю. Замену переменных можно осуществить следующим образом.