1.Выберем такую матрицу D типа ![]() что матрица
что матрица 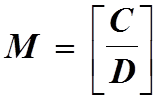 получается неособой.
получается неособой.
2.Матрицу М используем для следующего
преобразования вектора состояния Х в новый вектор ![]() согласно формуле
согласно формуле ![]()
3. Подставим в
формулу (3.20) выражение ![]() и получим новые
матрицы А и С, причем подбором элементов матрицы М матрицу
приведем к требуемой форме.
и получим новые
матрицы А и С, причем подбором элементов матрицы М матрицу
приведем к требуемой форме.
Теперь вектор состояния объекта можно представить в виде
![]()
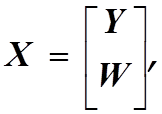 (3.21)
(3.21)
![]()
![]() где Y,W- векторы с
размерностями r и n-r.
Действительно, уравнение Y=CX, переписываемое
в этом случае как
где Y,W- векторы с
размерностями r и n-r.
Действительно, уравнение Y=CX, переписываемое
в этом случае как 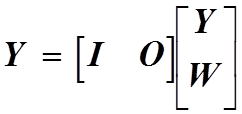 не лишено смысла и просто
означает, что Y=Y. Представляя матрицу А в блочной форме
не лишено смысла и просто
означает, что Y=Y. Представляя матрицу А в блочной форме
![]()
![]()
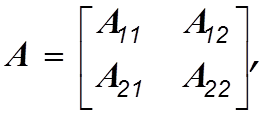 (3.22)
(3.22)
где
матрица ![]() имеет размер
имеет размер ![]() и учитывая (3.21), уравнения (3.20)
можно записать в виде системы
и учитывая (3.21), уравнения (3.20)
можно записать в виде системы
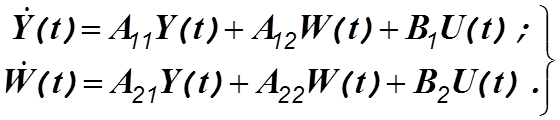 (3.23)
(3.23)
Идея синтеза редуцированного наблюдающего устройства
заключается в следующем. Выходной вектор объекта Y(t)доступен измерению, так что
дифференцированием можно получить его производную, являющуюся правой частью первого
уравнения системы (3.23). Так как вектор входных воздействий U(t)
тоже измеряемый, из указанного уравнения найдем вектор ![]() все
составляющие которого измеряемы. Отведем этому вектору такую же роль, какую
выполняет вектор СХ(t)в
правой части второго уравнения системы (3.20), а второе уравнение системы
(3.23) будем рассматривать как уравнение наблюдаемого объекта.
все
составляющие которого измеряемы. Отведем этому вектору такую же роль, какую
выполняет вектор СХ(t)в
правой части второго уравнения системы (3.20), а второе уравнение системы
(3.23) будем рассматривать как уравнение наблюдаемого объекта.
Это матричное уравнение характеризуется вектором
состояния W(t), представляющим
не поддающуюся непосредственному измерению часть вектора состояния исходного
объекта, и имеет в качестве измеримого внешнего воздействия ![]() Синтезируя наблюдающее устройство
идентификации для объекта, описываемого вторым уравнением системы (3.23), можно
оценить вектор W(t) и тем самым решить задачу оценки недостающих
составляющих вектора состояния X(t) исходного объекта. Если
система (С,А) полностью наблюдаема, то полностью наблюдаема и подсистема
Синтезируя наблюдающее устройство
идентификации для объекта, описываемого вторым уравнением системы (3.23), можно
оценить вектор W(t) и тем самым решить задачу оценки недостающих
составляющих вектора состояния X(t) исходного объекта. Если
система (С,А) полностью наблюдаема, то полностью наблюдаема и подсистема
![]() . Отсюда вытекает возможность синтеза
для объекта, характеризующегося вторым уравнением системы (23), наблюдающего
устройства идентификации порядка n-r с любыми желаемыми значениями корней.
. Отсюда вытекает возможность синтеза
для объекта, характеризующегося вторым уравнением системы (23), наблюдающего
устройства идентификации порядка n-r с любыми желаемыми значениями корней.
Выше
уже говорилось, что за выходной сигнал преобразованного объекта принимаем
сигнал ![]() Этот сигнал аналогичен сигналу
Этот сигнал аналогичен сигналу ![]() причем матрица
причем матрица ![]() выполняет
ту же роль, что и матрица С. Подставляя в общее уравнение наблюдающего
устройства идентификации вместо А,С,К соответственно
выполняет
ту же роль, что и матрица С. Подставляя в общее уравнение наблюдающего
устройства идентификации вместо А,С,К соответственно ![]() и L и учитывая,
что в наблюдаемом преобразованном объекте роль выходного сигнала Y
выполняет сигнал
и L и учитывая,
что в наблюдаемом преобразованном объекте роль выходного сигнала Y
выполняет сигнал 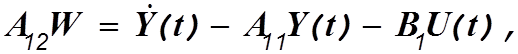 получим
следующее уравнение наблюдающего устройства (n-r)-го порядка:
получим
следующее уравнение наблюдающего устройства (n-r)-го порядка:
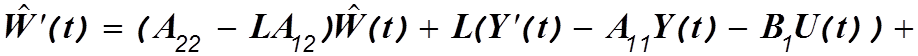
![]() (3.24)
(3.24)
Выбором матрицы L корням
наблюдающего устройства (3.24) можно придать любые желаемые значения. Когда
входной сигнал U(t) не доступен измерению, матрицу L
целесообразно выбирать из других соображений. Ее нужно брать такой, чтобы
передаточная функция ![]() обратилась в ноль. B этом
случае редуцированное наблюдающее устройство будет инвариантным в отношении приложенных
к объекту внешних воздействий.
обратилась в ноль. B этом
случае редуцированное наблюдающее устройство будет инвариантным в отношении приложенных
к объекту внешних воздействий.
Структурная схема наблюдающего устройства, соответствующая уравнению (3.24) показана на рис.3.6.
![]()
![]()
![]() Y
Y


![]()
![]()
![]()

![]() L
L
![]()
![]() U
U
|
|
|
|
|
 |
|||
![]()
![]()
![]()
Рис.3.6.Редуцированное наблюдающее устройство, использующее производные.
Дифференцирования вектора Y можно избежать, если точку суммирования перенести со входа интегратора на его выход. В результате получим окончательную структурную схему редуцированного наблюдающего устройства, приведенную на рис.3.7. Этой схеме соответствует уравнение
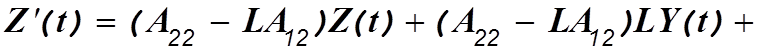
![]() (3.25)
(3.25)
где
![]() есть n-r вектор
состояния наблюдающего устройства, а
есть n-r вектор
состояния наблюдающего устройства, а ![]() -
его выходной вектор.
-
его выходной вектор.
![]()
![]()
![]()
![]()


![]()
![]() L
L
 |
|||||

![]()
![]()
![]() U
U ![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]() + +
+ + ![]() +
+ ![]()
![]()
![]()
![]()
Рис.3.7.Редуцированное наблюдающее устройство без дифференцирования.
Пример. Продолжим рассмотрение объекта, показанного на рис.5.
Этот объект представляет собой систему второго порядка с одним выходным
сигналом ![]() который будем предполагать
измеряемым. Для получения измеримой оценки второй переменной состояния
синтезируем редуцированное наблюдающее устройство первого порядка. Матрица С
уже имеет требуемую форму
который будем предполагать
измеряемым. Для получения измеримой оценки второй переменной состояния
синтезируем редуцированное наблюдающее устройство первого порядка. Матрица С
уже имеет требуемую форму 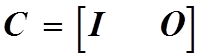 . Учитывая
(3.22), на основании (3.16-3.17) можно прийти к выводу, что входящие в систему
(3.23) матрицы в данном случае обращаются в скаляры
. Учитывая
(3.22), на основании (3.16-3.17) можно прийти к выводу, что входящие в систему
(3.23) матрицы в данном случае обращаются в скаляры
![]()
![]() (3.26)
(3.26)
Придадим наблюдающему устройству собственное значение -3, для чего, как это видно из (3.25) и(3.26), необходимо положить L=2. Приняв схему наблюдающего устройства, показанную на рис3.7, определим для звеньев этой схемы следующие передаточные функции:
![]()
Учитывая, что в принятой схеме наблюдающего устройства
роль сигнала y выполняет измеряемый выходной сигнал объекта ![]() ,приходим к схеме, приведенной на рис. 3.8.
,приходим к схеме, приведенной на рис. 3.8.
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]() 2
2


 u
u
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
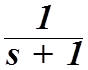
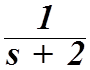 4 +
+
4 +
+ ![]() +
+
![]()


![]()
![]()
![]()
![]() 1
-3
1
-3
Рис.3.8. Редуцированное наблюдающее устройство с объектом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.