 |
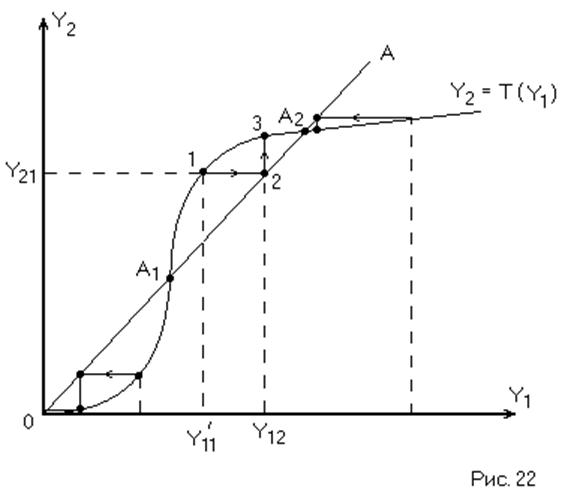
Характер процессов, происходящих в НСАР определяется
взаимным расположением диаграммы точечного преобразования [![]() ] и биссектрисы координатного угла,
уравнение которой Y2 = Y1.
Это означает, что после обхода вокруг начала (·) Y1
возвращается на своё место и, следовательно, в системе имеют место незатухающие
колебания (предельный цикл).
] и биссектрисы координатного угла,
уравнение которой Y2 = Y1.
Это означает, что после обхода вокруг начала (·) Y1
возвращается на своё место и, следовательно, в системе имеют место незатухающие
колебания (предельный цикл).
Область ниже биссектрисы ОА означает, что после обхода начала координат Y1 < Y1, т.е. колебания в системе затухают и фазовая траектория представляет закручивающуюся логарифмическую спираль (затухающие колебания).
Область выше биссектрисы ОА соответствует Y2 > Y1, и, следовательно, в этой области фазовые траектории представляют раскручивающуюся спираль (расходящиеся колебания).
Рассмотрим характер процессов в САР при любых начальных условиях:
![]() Точечное
преобразование точки
Точечное
преобразование точки ![]() - точка 1 (Рис. 22). К точке
1 применим ещё раз точечное преобразование, для чего найдём на оси абсцисс
значение
- точка 1 (Рис. 22). К точке
1 применим ещё раз точечное преобразование, для чего найдём на оси абсцисс
значение ![]() . Для этого проведём через точку 1
прямую, параллельную оси абсцисс до пересечения с биссектрисой (точка 2).
Точечное преобразование точки 2 – точка 3. Повторяя эти преобразования получаем
ступенчатую линию, приводящую нас в точку равновесия А2. Точки
касания ступенчатой линией биссектрисы ОА определяют последовательность точек
пересечения фазовой траекторией полуоси Y.
. Для этого проведём через точку 1
прямую, параллельную оси абсцисс до пересечения с биссектрисой (точка 2).
Точечное преобразование точки 2 – точка 3. Повторяя эти преобразования получаем
ступенчатую линию, приводящую нас в точку равновесия А2. Точки
касания ступенчатой линией биссектрисы ОА определяют последовательность точек
пересечения фазовой траекторией полуоси Y.
При начальных условиях Y0 = Y11 (справа от точки А2) точечные преобразования опять приводят нас к точке А2, следовательно точка А2 является точкой устойчивого равновесия и соответствует устойчивому предельному циклу.
Аналогичные рассуждения в окрестностях точки А1 показывают, что точка А1 является точкой неустойчивого равновесия (неустойчивый предельный цикл).
Итак, устойчивым предельным циклам соответствуют такие точки пересечения диаграммы точечного преобразования с биссектрисой Y2 = Y1, в которых диаграмма точечного преобразования имеет меньший наклон к оси абсцисс, чем биссектриса.
Аналитически это записывается так: 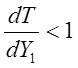 , т.к.
, т.к. ![]() биссектрисы
= 1. При
биссектрисы
= 1. При 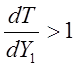 имеем неустойчивый предельный цикл.
Другими словами, устойчивый предельный цикл получается, если диаграмма
точечного преобразования пересекает биссектрису Y2
= Y1 сверху вниз, а неустойчивый – если
снизу вверх. Таким образом, кривая точечного преобразования позволяет
проанализировать возможные режимы поведения НСАР, а именно:
имеем неустойчивый предельный цикл.
Другими словами, устойчивый предельный цикл получается, если диаграмма
точечного преобразования пересекает биссектрису Y2
= Y1 сверху вниз, а неустойчивый – если
снизу вверх. Таким образом, кривая точечного преобразования позволяет
проанализировать возможные режимы поведения НСАР, а именно:
- система устойчива в малом, т.к. при Y1 < YA1 изображающая точка стремится к нулю;
- в системе возможен один предельный устойчивый цикл (точка А2).
 Зная координаты точки А2,
можно рассчитать частоту и амплитуду автоколебаний. При изменении параметров
НСАР диаграмма точечного преобразования перемещается относительно биссектрисы
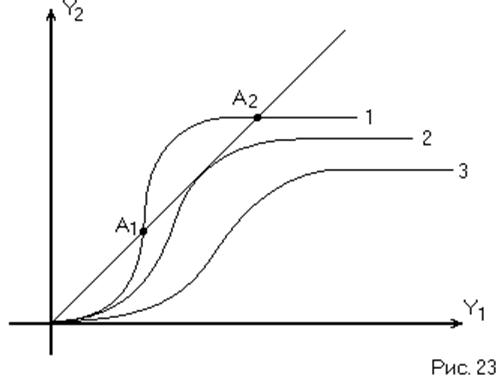
угла. При этом поведение НСАР может качественно меняться (Рис. 23).
Зная координаты точки А2,
можно рассчитать частоту и амплитуду автоколебаний. При изменении параметров
НСАР диаграмма точечного преобразования перемещается относительно биссектрисы
угла. При этом поведение НСАР может качественно меняться (Рис. 23).
Кривая 1, как мы видели ранее, соответствует устойчивости в малом и двум предельным циклам: устойчивому (А2) и неустойчивому (А1). Кривая 3 соответствует устойчивости в целом (ни одного предельного цикла). Кривая 2 касается биссектрисы и соответствует полуустойчивому предельному циклу. При изменении параметров НСАР мы переходим от кривой 2 к кривой 1 или 3, т.е. кривая 2 является границей между совершенно разными режимами работы НСАР. Значения параметров НСАР, при которых имеет место полуустойчивый предельный цикл, называются бифуркационными. (Бифуркация (лат.) – разделение, разветвление).
На рис. 24 изображена фазовая траектория системы
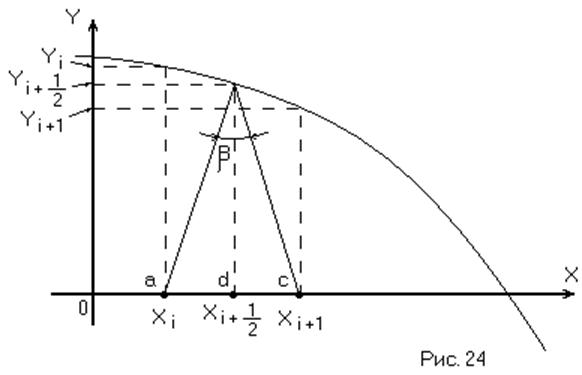
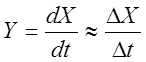 ;
; 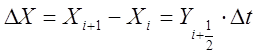
С другой стороны 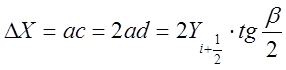 ,
,
отсюда 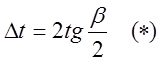
Из выражения ![]() вытекает
порядок построения переходного процесса:
вытекает
порядок построения переходного процесса:
1. Строим фазовую траекторию системы.
2. Задаёмся
промежутком времени![]() и находим
и находим 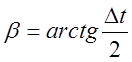 .
.
3. Из точки
начальных условий X0 вписываем в фазовую
траекторию равнобедренные треугольники с углом при вершине ![]() . Тогда, согласно выражению
. Тогда, согласно выражению ![]() , каждому
, каждому ![]() ,
заключённому в угле
,
заключённому в угле![]() , соответствует
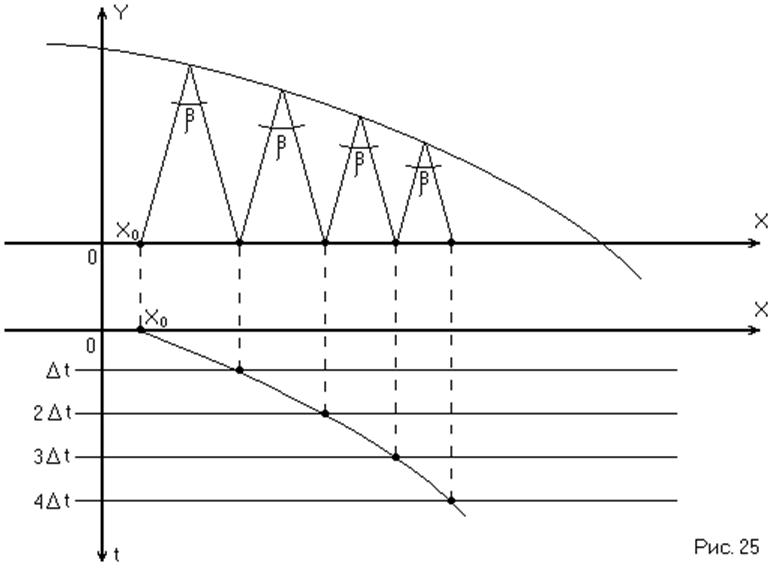
, соответствует ![]() . Следовательно, можно построить
переходный процесс (Рис. 25)
. Следовательно, можно построить
переходный процесс (Рис. 25)
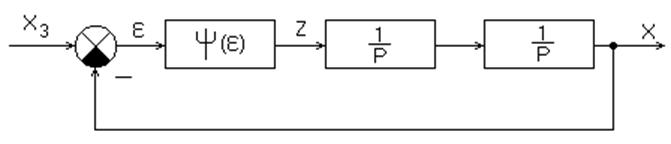
Структурная схема релейной САР изображена на рисунке:
Характеристика нелинейного элемента изображена на рис. 27
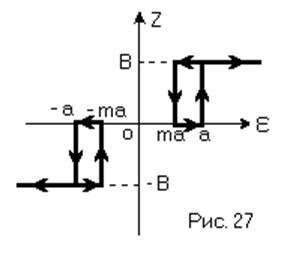
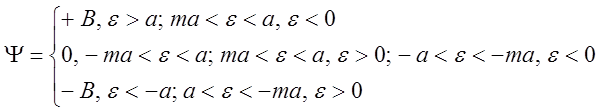
Запишем систему уравнений, описывающих поведение НСАР
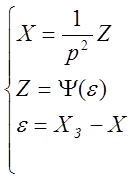 (1)
(1)
Рассмотрим свободное движение
НСАР, положив XЗ = 0. Тогда уравнение НСАР
запишется в виде ![]()
Оригинал дифференциального
уравнения системы 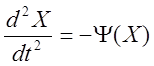 (2)
(2)
Найдём уравнение фазовой
траектории, исключив из уравнения (2) время. Для этого введём обозначение: 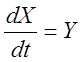 , тогда уравнение (2) запишется в
виде:
, тогда уравнение (2) запишется в
виде: 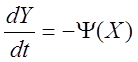 .
.
Разделив последнее уравнение на предыдущее, запишем дифференциальное уравнение фазовой траектории:
![]() (3)
(3)
Рассмотрим несколько случаев решения уравнения (3):
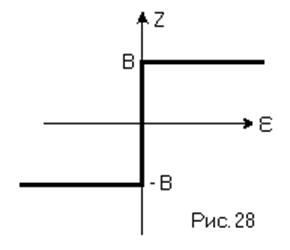 1)
1) ![]() . В этом случае характеристика
нелинейного элемента будет иметь вид, представленный на рисунке 28.
. В этом случае характеристика
нелинейного элемента будет иметь вид, представленный на рисунке 28.
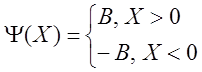
Решение уравнения (3) в данном случае будет иметь вид
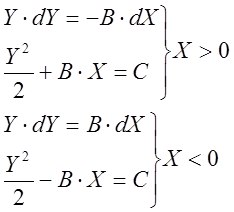
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.