Метод фазовой плоскости, страница 2

5)    - корни характеристического уравнения действительные, положительные, система неустойчива.

Уравнения изоклины и фазовых траекторий будут иметь вид

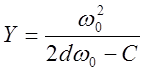, т.к.

, где

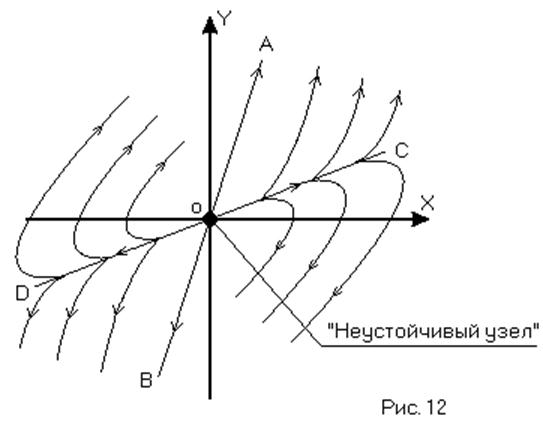
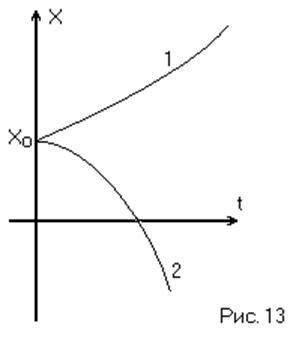
Фазовый портрет в этом случае как бы переворачивается, особая точка называется «неустойчивый узел» (Рис. 12), а все переходные процессы апериодические, расходящиеся (Рис. 13). Внутри угла AOC (BOD) переходные процессы монотонные, вне этого угла – с одним перерегулированием. (Рис. 13).

                  

Рассмотрим, так называемые, вырожденные случаи уравнения второго порядка:

6)  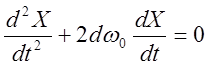         , где (отрицательный действительный корень)

Уравнение  - уравнение астатического (интегрирующего) звена, которому соответствует состояние безразличного равновесия. Уравнение фазовой траектории получим следующим обрвзом:

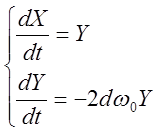
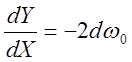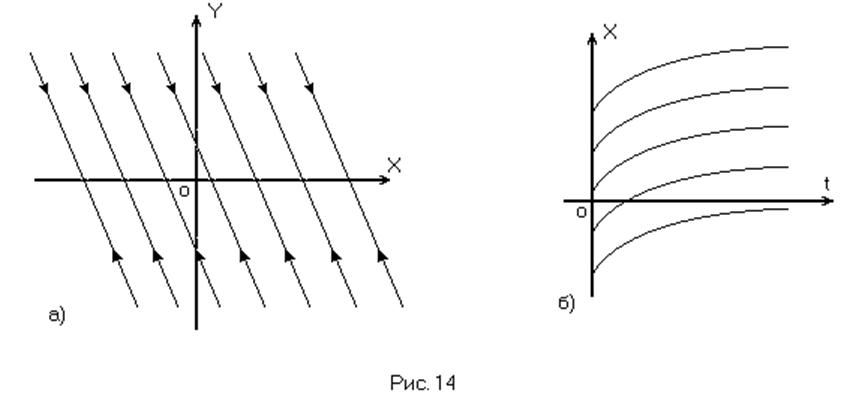
Поделив второе уравнение этой системы на первое, получим , тогда , т.е. в данном случае существует не одна точка равновесия, т.е. равновесие наступает при любых X, это и есть безразличное равновесие. (Рис. 14а и 14б)

7) Если же , то вырожденное уравнение второго порядка будет иметь вид:

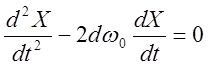, где .

Уравнение фазовой траектории в этом случае может быть получено следующим образом:

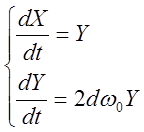 и тогда , .

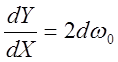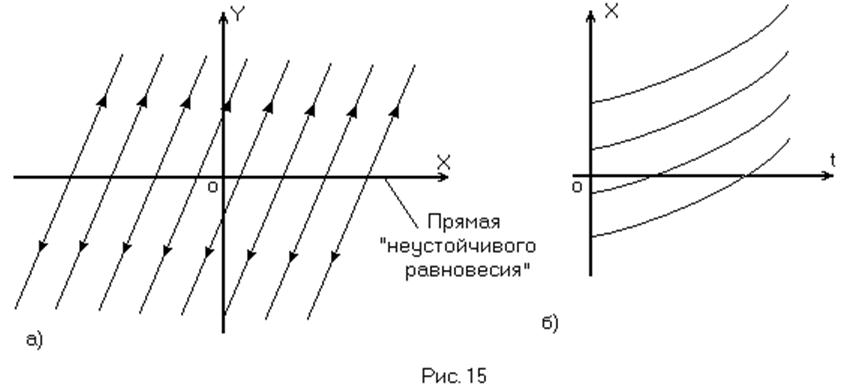
В данном случае имеем прямую неустойчивого равновесия в фазовой плоскости и расходящийся переходный процесс. (Рис. 15а и 15б).

8) , а дифференциальное уравнение имеет вид: 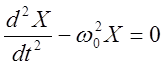; т.е. корни характеристического уравнения действительные, разного знака.

Найдём уравнение фазовой траектории для этого случая

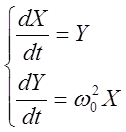
Поделив второе уравнение системы на первое, получим 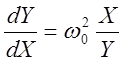. Решив это дифференциальное уравнение найдём уравнение фазовой траектории:

, тогда

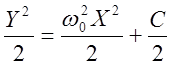  , т.е.  - уравнение фазовой траектории.

Уравнения изоклин найдём следующим образом: 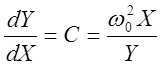. Отсюда  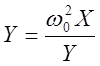 - уравнение изоклин. Изоклины в данном случае – прямые, проходящие через начало координат (Рис. 16). Фазовые траектории получим из выражения , где .

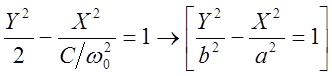  - уравнение гиперболы, асимптоты которой .

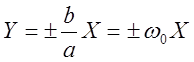В случае , когда , имеем семейство сопряжённых гипербол, описываемых уравнением

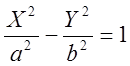
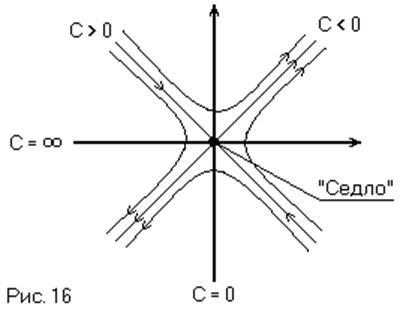
Во всех, кроме одного случая изображающая точка уходит в бесконечность, и только при движении по асимптоте  она движется к положению неустойчивого равновесия. Малейшее отклонение от этой траектории уводит изображающую точку в бесконечность. Точка неустойчивого равновесия является особой точкой типа «седло».

Рассмотрев фазовые портреты кусочно-линейного звена, т.е. линейного на каждом участке, можно сделать вывод:

Если рассматривать нелинейные системы, то полученный фазовый портрет справедлив лишь при малых отклонениях от состояния равновесия, в том числе и от особой точки типа «седло». В последнем случае асимптоты являются прямыми лишь при малых отклонениях, а при больших отклонениях они становятся кривыми линиями. Эти кривые исходящие из особой точки типа «седло» называются «сепаратрисами». Они делят фазовую плоскость на сепаратные области. (Рис. 17)

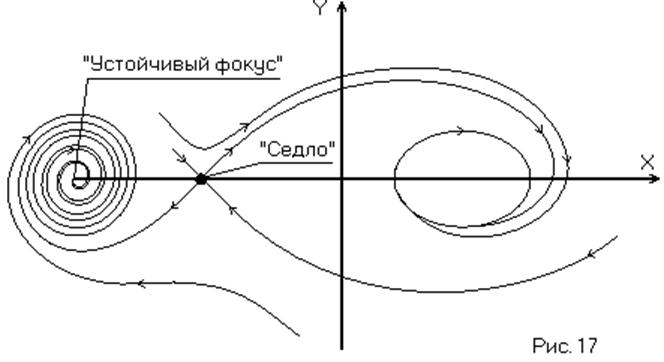
Задачи с сепаратрисами встречаются редко и в дальнейшем рассматриваться не будут.

IV.  Предельные циклы

Мы рассмотрели два типа особых траекторий: особые точки и сепаратрисы. Очень важным видом особой траектории является «предельный цикл». В линейной системе второго порядка описываемой дифференциальным уравнением (1), при  имеем замкнутую фазовую траекторию (эллипс), которую мы не можем отнести к предельным циклам, т.к. в этом случае имеем в системе не автоколебания, а границу устойчивости линейной системы. Во всех остальных случаях изолированные, замкнутые фазовые траектории принято называть предельными циклами.

Предельный цикл соответствует устойчивому периодическому режиму – автоколебаниям, если все фазовые траектории «наматываются» на предельный цикл (устойчивый предельный цикл) (Рис. 18).

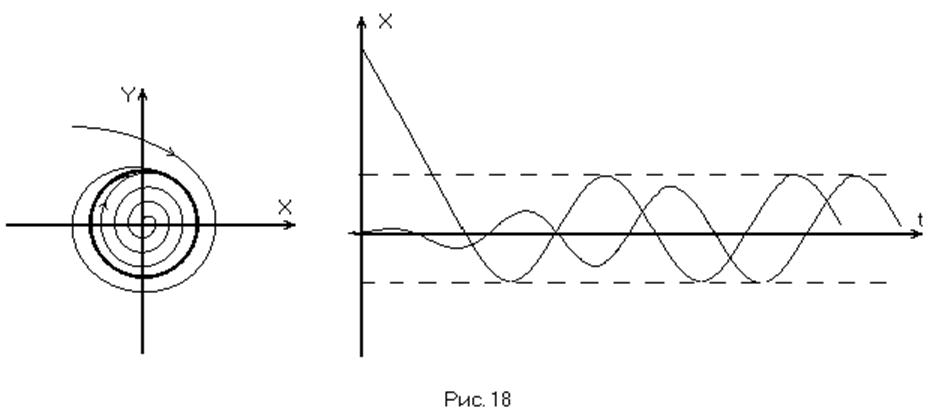
Если же все фазовые траектории «сматываются» с предельного цикла, как изнутри, так и снаружи, такой предельный цикл неустойчив и соответствует неустойчивым автоколебаниям. (Рис. 19).

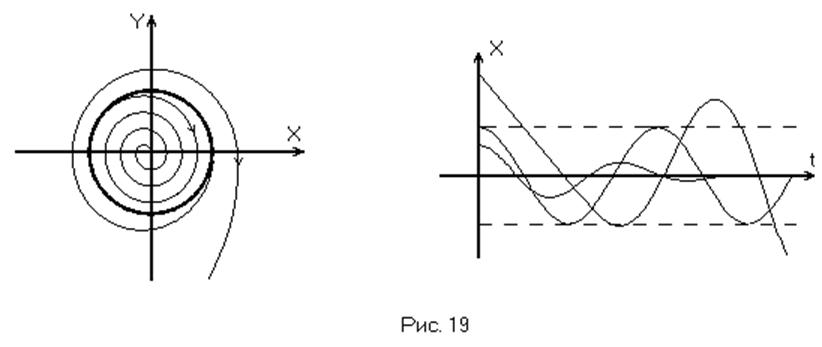
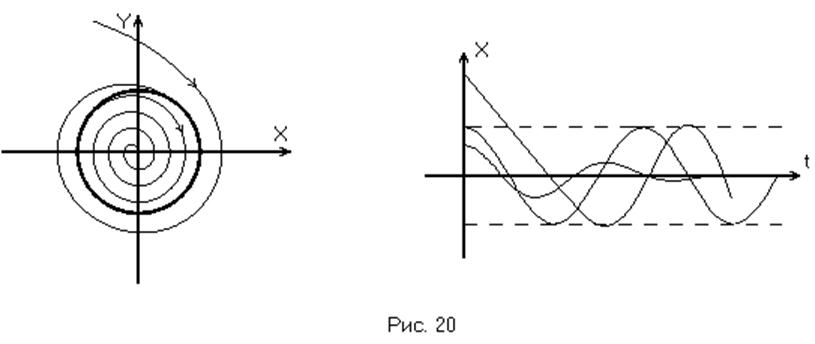
Если же соседние траектории «навёртываются» на предельный цикл с одной стороны и «свёртываются» с другой, такой предельный цикл называется полуустойчивым. (Рис. 20).

Итак, при исследовании НСАР особыми траекториями являются «особые точки» (положение равновесия) и предельные циклы (устойчивые периодические колебания). Они и составляют схему фазового портрета.

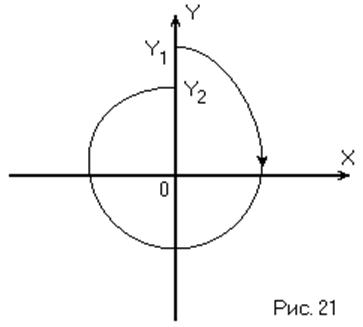V.  Метод точечного преобразования

Метод точечных преобразований предложен академиком Андроновым и является дополнением к методу фазовой плоскости. Он служит для анализа возможных режимов в НСАР и их количественной оценки. Пусть изображающая точка в какой-то момент времени находится на верхней полуоси ординат (· Y₁). При движении изображающей точки по фазовой траектории она обходит начало координат и снова возвращается на полуось (· Y₂). (Рис. 21)

При этом «Y₂» может быть больше, меньше или равно «Y₁». Операция нахождения точки Y₂ по заданной точке Y₁ называется точечным преобразованием.

Аналитическое взаимно однозначное и непрерывное соответствие точек Y₂ с точками Y₁ на одной и той же полупрямой (т.е. точечное преобразование) устанавливается с помощью так называемой функции последования, которая может быть получена из уравнения фазовой траектории

         (14)

С помощью этой зависимости можно осуществить точечное преобразование всех точек положительной полуоси ординат, или, другими словами, точечное преобразование положительной полуоси Y, в саму себя.