Методические указания по расчету закрытых передач для студентов инженерно-технических специальностей в курсовых и дипломных проектах, страница 6

d_e2  = m_e× Z ₂.                                        d_e2  = m_te× Z ₂.

3.6.6. Внешний диаметр вершин зубьев шестерни и колеса

d_ae1 = d_e1 + 2×(1+X_e1) ×m_e × cos δ₁;           d_ae1 = d_e1 +1,64× (1+X_n1 ) ×m_te ×cos δ₁;

d_ae2  = d_e2 + 2×(1+X_e2) × m_e×cos δ₂.           d_ae2 = d_e2 +1,64× (1+ X_n2  ) ×m_te ×cos δ₂.         

Коэффициенты смешения X_e  и X_n следует принимать по таблицам А.9 и А.10. Для передач, у которых значения Z₁ и  находятся в интервалах между указанными значениями в таблице А.9 и А.10,  коэффициенты смещения принимают по верхней границе интервала, например: в таблице      А.10     при Z₁ = 17 используют Z₁ = 18.

          Коэффициент смещения инструмента при нарезании зубьев колес [4, с.122] принимается равным:

X_e2 = – X_e1 .                                |                X_n2  = – X_n1.

3.6.7 Внешний диаметр впадин зубьев  шестерни и колеса

d_fe1 = d_e1 - 2×(1,2-X_e1)×m_e × cos δ₁;        d_fe1 = d_e1 –1,64× (1,25–X_n1 ) ×m_te ×cos δ₁;

d_fe2  = d_e2 - 2×(1,2-X_e2)×m_e ×cos δ₂.         d_fe2 = d_e2 –1,64× (1,25– X_n2  ) ×m_te ×cos δ₂.

3.6.8 Среднее конусное расстояние R_m

R_m = R_e – 0,5× b₂ , мм.

3.6.9 Модуль средний расчетный m_m , m_mn

здесь  βm = 29-450 , для расчетов  принято βm = 350;   .

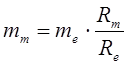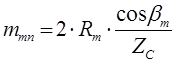, мм.                                   , мм;

3.6.10 Средний делительный диаметр шестерни d₁ и  колеса d₂

d₁ = m_m×Z ₁ ;                                  ;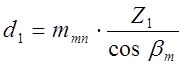

d₂ = m_m×Z ₁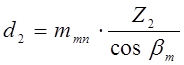, мм.                            , мм.

3.6.11 Окружная скорость в конической передаче

Окружная скорость определяется исходя из среднего делительного диаметра шестерни d₁

, м/с.

3.7 Проверочный расчет зубьев колес передачи

3.7.1 Проверочный расчет зубьев колес на контактную выносливость

Расчетное контактное напряжение ( МПа) определяется формулой:

.

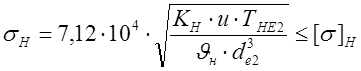Определение перегрузки (недогрузки) в процентах:

.

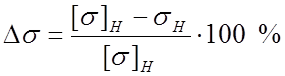          Перегрузка возможна до 5 % (по модулю), недогрузка – до 10…12 %. При превышении установленных значений  следует изменить диаметр внешней делительной окружности колеса  в соответствии со стандартным рядом (см. п.3.1) и расчет передачи повторить начиная с п.3.2.

3.7.2 Проверочный расчет зубьев колес на изгибную выносливость

3.7.2.1 Расчетное напряжение изгиба в опасном сечении зуба колеса σ_F2

где К_F – коэффициент нагрузки при изгибе (см.п.2.6.6);

T_FE2  – эквивалентный вращающий момент, Н×м  (см. п.2.7);

 – коэффициент прочности зуба колеса (см. таблицу А.8);

b₂ – ширина колеса, мм;

m_e, m_te – модули внешний окружной для передачи с прямыми и круговыми зубьями соответственно, мм;

[σ]_F2 –допускаемое напряжение материала колеса на изгиб (см.п.2.5);

Y_F2 – коэффициент формы зуба колеса, определяют в зависимости от эквивалентного числа зубьев Z_v  и коэффициента смещения инструмента Х по формуле:

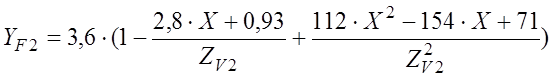, здесь  Z_V2 – эквивалентное число зубьев колеса:

Z_V2 = Z₂ / cos δ ₂ ,                               |         Z _{V n 2} = Z₂ / (0,55×cos δ ₂);

X – коэффициент смещения инструмента.

3.7.2.2 Расчетное напряжение изгиба в опасном сечении зуба шестерни

.

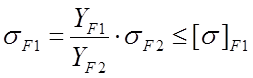Значение Y_F1 и [σ] _F1 находят аналогично определению этих параметров для колеса.

3.7.3 Расчет передачи на кратковременную пиковую нагрузку

Определяем коэффициент перегрузки привода

.

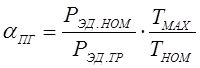При   > 2  производят проверку только на  пиковую контактную выносливость, а при  > 3 – проверяют и на контактную выносливость и выносливость зубьев на изгиб при пиковой нагрузке.

Максимальное контактное напряжение на рабочих поверхностях зубьев _Нmах:

, где []_Hmах – максимальное допускаемое контактное напряжение рассчитывается по пределу текучести материала колеса,  МПа:

[]_Hmах = 2,8× _Т2, здесь σ_Т2 – предел текучести материала колеса.

Максимальное напряжение изгиба в основании зуба  колеса σ_{Fmax 2}:

, где []_Fmax2 – максимальное допускаемое напряжение изгиба для материала колеса, МПа:

[]_{F max 2} = 2,74×НВ_ср2, здесь  НВ_ср2 – средняя твердость материала зуба колеса.

3.8 Силы, действующие в зацеплении  конических колес