Методические указания по расчету закрытых передач для студентов инженерно-технических специальностей в курсовых и дипломных проектах, страница 5

Коэффициент нагрузки при расчете на изгибную выносливость

K_F = K_Fβ × K_HV , где   K_Fβ  - коэффициент концентрации нагрузки на изгиб (см. п.2.6.3.2);

K_HV – коэффициент динамичности нагрузки при изгибе (см. п.2.6.5).

          2.7 Эквивалентные вращающие моменты на валу колеса T_HE2, T_FE2

T_HE2 = K_HД × Т₂;     Т_FE2 = К_FД × T₂, Н×м, где  К_НД и К_FД – коэффициенты долговечности (см.п.п.2.6.4).

3 Проектный и проверочный расчеты  передачи

          Геометрические параметры конических зубчатых колес определяют по ГОСТ 19624-74 для передач с прямыми зубьями и по ГОСТ 19326-73 для передач с круговыми зубьями.

3.1 Диаметр внешней делительной окружности колеса

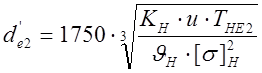           ,мм, где К_Н – коэффициент нагрузки (см. п. 2.6.6.);

Т_НЕ2 – эквивалентный крутящий момент на валу колеса, Н×м (см. п. 2.7.);

[σ]_Н – допускаемое контактное напряжение, МПа (см. п. 2.5.);

– коэффициент прочности зуба колеса, принимают по таблице А.8.

Полученное расчетом значение  округляют до ближайшего значения из ряда стандартных чисел (мм) по ГОСТ 12289-76, окончательно принимая значение :

1-й ряд: 50; 63; 80;100; 125; 160; 200; 250; 315; 400; 500; 630; 800; 1000; 1250…

2-й ряд: 56; 71; 90; 112; 140; 180; 225; 280; 355; 450; 560; 710; 900; 1120;1400…

Стандартные значения   можно при необходимости  продолжить [6, c.49] .

          3.2 Диаметр внешней делительной окружности шестерни 

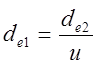          , мм.

Полученное значение  не округлять.

3.3 Число зубьев шестерни

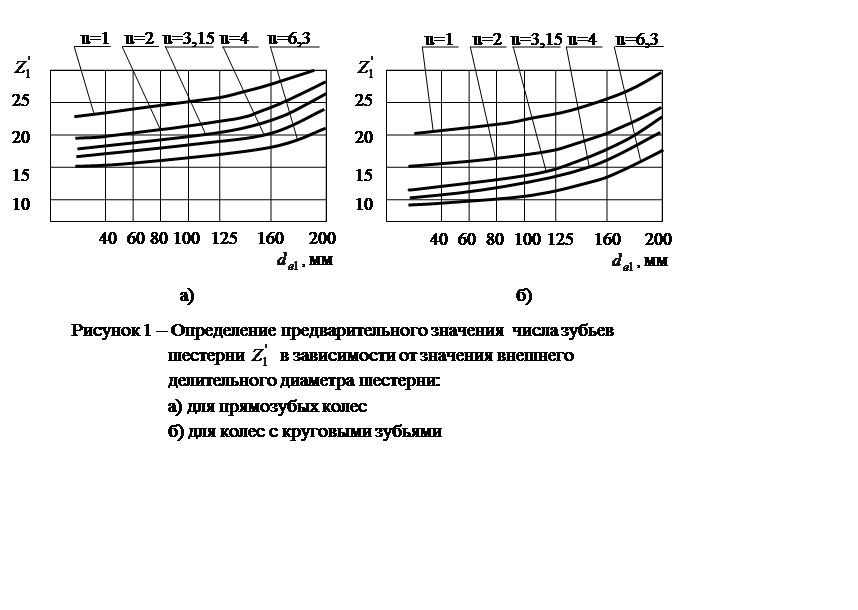По рисунку 1 в зависимости от диаметра внешней делительной окружности шестерни  и предварительного значения передаточного числа передачи  определяем  предварительное число зубьев шестерни .

По полученному по графикам в соответствии с рисунком 1 значению  определяют окончательное значение числа зубьев шестерни в зависимости от вида термической обработки материалов шестерни и колеса:

 

 − если шестерня и колесо выполнены из материалов   первой группы (твердость зубьев шестерни и колеса меньше 350 НВ);

− если шестерня выполнена из материала  второй группы (твердость зубьев шестерни больше 350 НВ), а колесо − из материала  первой группы (твердость зубьев колеса меньше 350 НВ);

− если шестерня  и колесо выполнены из материала  второй группы (твердость зубьев шестерни  и колеса больше 350 НВ).

Значение округляют до целого числа.

3.4 Число зубьев колеса

 

Значение также округляют до целого числа.

3.5 Фактическое передаточное число

          .

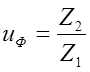Отклонение фактического передаточного числа от первоначально заданного:

.

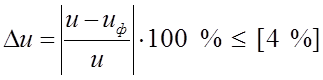3.6 Геометрические размеры передачи

3.6.1 Модуль внешний окружной

m_e = d_e2 / z₂  , мм.                           m_te = d_e2 / z₂  , мм.

Для силовых передач принимать модуль m_e(m_te) менее 1,5 мм не желательно [1, с.50]. Полученный модуль называют производственным и округлять его до стандартного значения не обязательно.

Здесь и далее, если запись  ведется двумя колонками, то в левой колонке записаны расчетные формулы и расчеты для конической передачи с прямыми зубьями, а в правой – для конической передачи с круговыми зубьями. Если разделения по колонкам нет, то формулы и расчеты одинаковы для обоих типов конических передач.

3.6.2 Углы делительных конусов колеса и шестерни δ₂ , δ₁

δ₂ = arctg ,   δ₁ = 90⁰ – δ₂ , град.

3.6.3 Внешнее конусное расстояние

.

3.6.4 Ширина колеса и шестерни

b₂ = b₁ =   , где = 0,285 – коэффициент ширины зубчатого венца по внешнему конусному расстоянию по ГОСТ 12289-76.

Полученное значение можно округлить до ближайшего целого значения, желательно из стандартного  ряда R_a20 ГОСТ 6636-69 (приведен с сокращениями): 12; 14; 16; 18; 20;  22;  25;  28; 32; 36; 40; 45; 50; 56; 63; 71; 80; 90; 100.  В случае необходимости могут использоваться    значения   из  ряда  R_a40 и из дополнительного ряда  ГОСТ6636-69.

3.6.5 Диаметр внешней делительной окружности шестерни и колеса

           d_e1  = m_e ×Z₁ ;                                        d_e1  = m_te ×Z₁ ;