Уравнение Слуцкого. Экономическое значение, страница 7

Т.е  в данной задаче при заданном бюджетном ограничении потребительский набор, максимизирующий функцию полезности равен (3,1).

Функция спроса модели Стоуна имеет вид:

x_i= x_i⁰+ a_i (I - p_j x_j⁰) / [p_ia_j] , где i = 1..n – вид товара.                        (26)

Эту функцию легко интерпретировать. Вначале приобретается минимально необходимое количество каждого блага a_i. Затем рассчитывается сумма денег, оставшаяся после этого, которая распределяется пропорционально «весам» важности α_i. Разделив количество денег на сумму р_i, получаем дополнительно приобретаемое, сверх минимума, количество i – го блага и добавляем его к а_i.

Используя формулу, получаем функции спроса:

x₁= 3+0, 5*(40-5*3-1*1)/(5*(0, 5+0,67)) = 7,1

x₂= 1+0,67*(40-5*3-1*1)/(1*(0, 5+0,67)) = 9,74.

То есть х₁=7.1 и х₂=9.74 – это набор продуктов, которые можно приобрести не превышая доход.

Далее находим фукцию бюджетного ограничения:

   ;                                                                          (27)

9,74-1) ==2,02*4,27=8,62

Выводим формулу  кривой безразличия x^u₂:

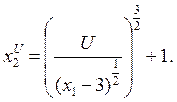                                                                       (28)

Выводим формулу кривой безразличия максимальной полезности при U=8.62:

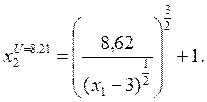
Выводим формулу кривой безразличия при U=3

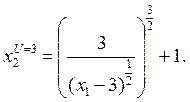
Выводим формулу кривой безразличия при U=1

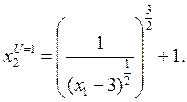
Далее составим таблицу с допустимым множеством значений и построим кривые безразличия и прямую бюджетного ограничения.

Таблица 2.

x1	4	5	6	7	8	9	10
x2бюдж	20	15	10	5	0	-5	-10
x2U=max	24,52419	14,98757	11,31986	9,317058	8,568911	7,136225	6,466272
x2 u=7	19,52026	14,0958	11,69268	10,26013	9,282512	8,560864	8
x2 u=6	15,69694	11,3923	9,485281	8,348469	7,572671	7	6,554921

На рисунке 3 изображены графики бюджетного ограничения и кривых безразличий.

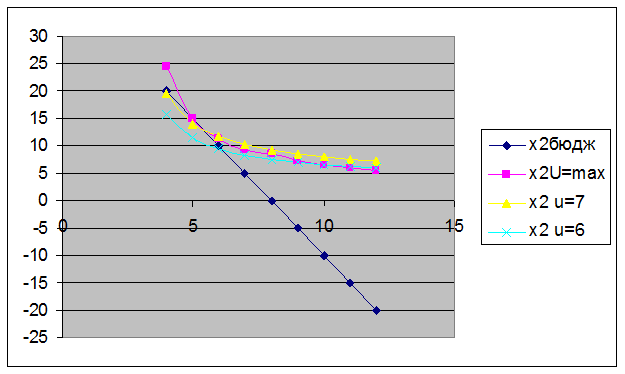
Рисунок 3.

Бюджетное ограничение и функции безразличий

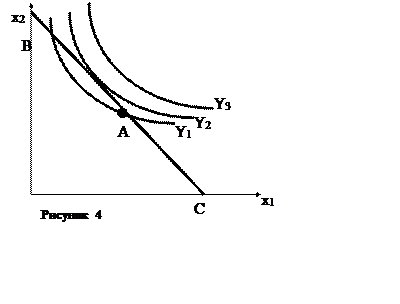
Задача 4

На графике изображены карта кривых безразличия производственной функции, показывающая возможные уровни производства при различных сочетаниях ресурсов: труда (x₁) и капитала (x₂). Точка А - показывает реальное сочетание ресурсов (технологический способ). ВС – линия бюджетного ограничения, показывает множество комбинаций ресурсов, расходы на покупку которых одинаковы.

 

Отметьте на графике точку, соответствующую ситуации:

Задание 19: Оптимальный уровень производства при условии, что уровень заработной платы повысился в 1,5 раза, а плата за капитал осталась прежней.

Решение:

Изобразим графически на рисунке 5:

капитал

Рисунок 5.                              

На рисунке 5 Оптимальное сочетание ресурсов, дающее максимальную прибыль, достигается в точке D касания линии бюджетного ограничения и кривой безразличия Y₃. Новая линия бюджетных ограничений ВС₁ соответствует условиям задачи. Так как, по условию задачи,  уровень заработной платы повысился в полтора раза, а плата за капитал осталась прежней, отрезок ОС₁ в 1,5 раза длиннее отрезка ОС, о отрезок ОВ не изменился.