Уравнение Слуцкого. Экономическое значение, страница 3

Говоря более строго, эффект дохода Δxⁿ₁, есть изменение спроса на товар 1при изменении дохода с т' до т и сохранении цены товара 1 постоянной на уровне p₁' :

Δxⁿ₁= x₁(p₁',m) – x₁(p₁',m').                                                                     (6)

Эффект дохода может действовать двояким образом: он ведет либо к повышению, либо к понижению спроса на товар 1 в зависимости от того, о каком товаре идет речь — нормальном или низшей категории.

При снижении цены необходимо уменьшать доход, чтобы сохранить покупательную способность постоянной. Если товар — нормальный, то такое уменьшение дохода приведет к сокращению спроса. Если товар является товаром низшей категории, уменьшение дохода приведет к увеличению спроса[1, стр. 163].

1.3.  Общее изменение спроса

Общее изменение спроса Δx₁ есть изменение спроса, вызываемое изменением цены при сохранении дохода постоянным:

Δx₁= x₁(p₁',m) – x₁(p₁,m).                                                                             (7)

Это изменение можно подразделить на два изменения: эффект замещения и эффект дохода. Или, пользуясь принятыми выше обозначениями:

Δx₁= Δx^S₁+ Δxⁿ₁                                                                                            (8)

Если выразить смысл данного уравнения словами, то оно говорит о том, что общее изменение спроса равно сумме эффекта замещения и эффекта дохода. Это уравнение называется тождеством Слуцкого.

Суть тождества Слуцкого состоит не в том, что оно представляет собой алгебраическое тождество — это математическая тривиальность. Суть данного тождества заключается в интерпретации двух членов в правой части: эффекта замещения и эффекта дохода. В частности, мы можем применить то, что нам уже известно о знаках эффектов дохода и замещения, чтобы определить знак общего эффекта.

2.  Математическое значение уравнения Слуцкого

Одним из основных в теории потребительского выбора является уравнение Слуцкого.

Это уравнение позволяет увязать действие эффекта дохода с результирующим изменением спроса.

Основное матричное уравнение:                

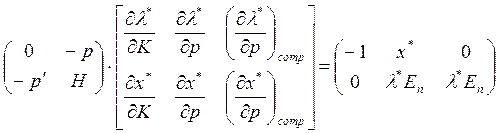 можно записать следующим образом:

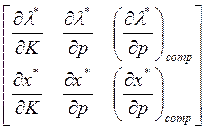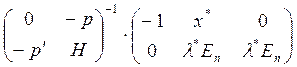=                           (9)

Решение этой системы относительно показателей сравнительной статики по спросу имеет вид:

(12)

(10)

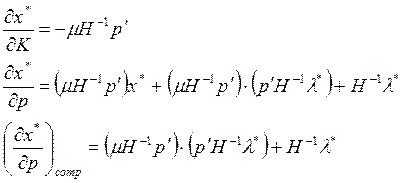                (11)

Здесь  - обратная матрица Гессе, а  - скалярная величина. Можно показать, что 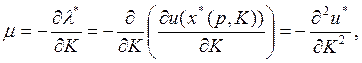 поэтому скаляр  можно интерпретировать как коэффициент убывания предельной полезности денег.

Сравнивая (11) и (12) замечаем, что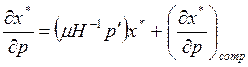

Сопоставляя это уравнение с (10), получаем

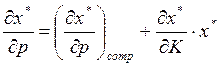                                                                (13)

Равенство (13) называется уравнением Слуцкого. Это же уравнение называют основным уравнением теории ценности.

В координатной форме уравнение Слуцкого выглядит так:

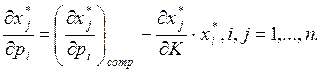                                          (14)

Первое слагаемое в правой части описывает действие эффекта замены (т. е. компенсированное изменение цены на спрос), второе – действие эффекта дохода (влияние изменения дохода на спрос), выраженное в тех же единицах измерения. Слева записано результирующее воздействие на спрос, складывающееся из изменения структуры спроса и общего его изменения при изменении уровня реального дохода.

Перепишем уравнение следующим образом:

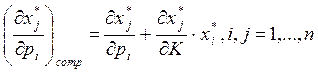                                           (15)

Из (4) следует, что матрица влияния замены симметрична и отрицательно определена. Из отрицательной определенности следует

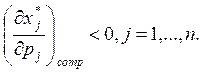                                                                        (16)

Отсюда вывод 1– компенсированное возрастание цены товара приводит к уменьшению спроса на этот товар.

Из симметричности матрицы влияния замены и уравнения (15) получаем: