Краткие теоретические сведения и методические советы по выполнению курсовой работы, страница 9

,                                         (2.17)

Если порядок уравнения (2.6) больше двух, то расчет ПХ, методом дифференциальных уравнений оказывается громоздким и неудобным. В этом случае целесообразно применить операторный метод.

2.3. Переходная характеристика, в соответствии с ее определением (2.1), найденная классическим методом, в общем виде, определяется выражением:

                                     (2.18)

2.4.    Временными параметрами характеризующими ПХ являются - постоянная времени t, и время установления t_уст.

Постоянная времени, вводится для экспоненциальной функции вида:

y= e ^pt  , где p<0. Постоянная времени  характеризует скорость изменения экспоненциальной функции на начальном этапе. Под постоянной времени цепи понимают время за которое выходной сигнал изменившегося по закону  y = e ^pt уменьшается  в e=2,71 - раз, т.е. до уровня 1/e = 0.37 от своего начального значения.

Время установления - это время за которое переходная характеристика достигает своего стационарного значения с заданной точностью. Функции уменьшающаяся по закону y=ехр(t/t)  за время 3t достигает своего стационарного значения с точностью 5%. Если нет особых оговорок то за время установления и принимают 3t. (t_уст =3t).

Рассмотрим цепь первого порядка.

1. Для цепи 1-ого порядка составленное дифференциальное уравнение имеет вид:

        ,

2. общее решение неоднородного ЛДУ известно

 ,

 где  - общее решение однородного дифференциальное уравнения, когда .

Его решение известно, оно имеет вид - ; -частное решение неоднородного ЛДУ

3.Найдем частное решение неоднородного ЛДУ. Его вид зависит от правой части неоднородного уравнения, т.е. от воздействующего сигнала. Если входной сигнал - ступенчатая функция Е1(t), то при t®¥ его можно считать постоянной величиной, а потому за  принять , и находить, как отклик цепи на входной сигнал постоянной величины E, считая его гармоническим сигналом с нулевой частотой (Е=Еcosωt|_ω=0). Отсюда общее решение имеет вид:

_.

4. p_i –определяют как корни характеристического уравнения. Оно для дифференциального уравнения первого порядка имеет вид-  tp₁+1=0, отсюда .

5. A₁ –произвольная постоянная, определяется из начальных условий самой функции и ее производных.

Найдем А₁. При , . Значение y(0) находится из начальных условий при t=0, используя законы коммутации или из схемы замещения исходной цепи при ω®¥.

6. Отсюда общее решение для цепи первого порядка имеет вид

.

Пример 2.1: Для схемы приведенной на рис.2.2  найти - 

Порядок решения:

1.Составим дифференциальное уравнение относительно U₂=U_c1 и приведем его к стандартному виду:

          

     

.                        

2. Запишем общее решение: , _.т.е  .

3. Найдем  из схемы замещения (рис.2.3) исходной цепи при t®¥ (когда ω=0). Получим .

4. Найдем корень характеристического уравнения

.

5. Найдем y(0) из схемы замещения (рис.2.4) исходной цепи при t®0 (когда ω®¥). Учитывая, нулевые начальные условия и закон коммутации для емкости, получим y(0)=0

6. Запишем окончательное решение:

 

График ПХ приведен на рис.2.5

Переходная характеристика имеет 2 параметра:

1) постоянная времени - время за которое переходная характеристика достигает уровня 0.63 от своего стационарного значения: .

2) время установления: t _{уст. 1%}=5τ,     t _{уст. 5%=}3τ.

Пример 2.2. Рассчитать переходную характеристику двухконтурной цепи рис.2.6.

U₁(t)=E₁(t) ,      U₂(t)=h(t)=?

 ,       

1. Составим дифференциальное уравнение и приведем его к стандартному виду.

Уравнение будем составлять, относительно тока второго контура i₂ , используя метод контурных токов, а в конце найдем U₂=L(di₂/dt). По методу контурных токов запишем систему, после показанных ниже преобразований сведем ее к дифференциальному уравнению второго порядка

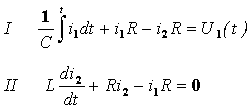
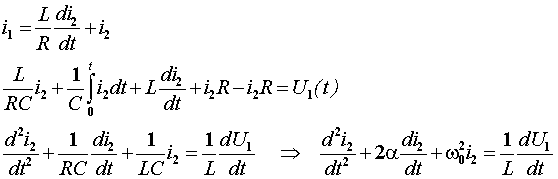
2.Общее решение относительно тока i₂ имеет вид:        

1.  Найдем i₂(∞) из схемы замещения (рис.2.7) при t®¥, когда ω=0. Получим i₂(∞) =0.