Краткие теоретические сведения и методические советы по выполнению курсовой работы, страница 3

5.  Если необходимо, то перейти от комплексных амплитуд интересующих токов и напряжений к гармоническим функциям времени (y(t)=Y_mcos(ωt-φ_y)).

Для цепи второго порядка КЧХ в общем случае можно записать в виде

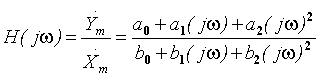.                                                      (1.11)

Выделим в числителе и знаменателе действительную и мнимую части, приведем подобные члены, и запишем  в показательной форме

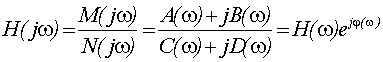.                          (1.12)

Отсюда получим выражения для расчета амплитудно-частотных (АЧХ) и фазо-частотных (ФЧХ) характеристик

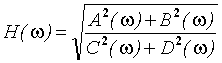
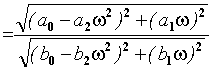                                        (1.13)

φ(ω)=φ_числ(ω)–φ_знам(ω),                                                    (1.14)

1.5. Построение графиков частотных характеристик

При графическом изображении частотных характеристик электрической цепи обычно строят отдельные графики АЧХ и ФЧХ цепи. Графики функции, заданной формулой Н(ω) строятся по точкам, в определенном диапазоне частот, в котором проявляются основные свойства электрической цепи, которые затем соединяются плавной линией.

Выбор диапазона частот.

Для оценки частотного диапазона, в котором необходимо построить графики частотных характеристик цепи, определим особые точки операторной передаточной функции. Для этого заменим в формуле (1.11) =p, получим операторный коэффициент передачи по напряжению

.                                                    ()

Особыми точками (нулями и полюсами) K_u(p) являются значения аргумента (нули), при которых M(p)=0, и значения аргумента  (полюсы), при которых N(p)=0, где i=1,2.. порядковый номер особой точки. Для наглядности их изображают в комплексной плоскости, комплексной частоты р=a+jw. Нули изображают кружочками, а полюсы крестиками.

За частотный диапазон можно принять интервал между  и

;         , где  - расстояние от начала координат до ближайшей особой точки, которое определяется ее модулем, т.е. =min{||,||};  - расстояние до самой удаленной особой точки, т.е. =max{||,||}, где модуль комплексной частоты определяют по формуле |p|=.

Выбор масштаба построения графиков. При построении графиков частотных характеристик применяют различные масштабы по осям (вертикальной – ось ординат и горизонтальной – ось абсцисс): абсолютный (линейный) масштаб по осям применяют, если диапазон изменения величины не более одной декады, и логарифмический, если диапазон изменения величины составляет две и более декады. На практике часто используется полулогарифмический масштаб, когда по горизонтальной оси берется логарифмический масштаб, а по вертикальной – линейный.

В тех случаях, когда предполагаемая частотная характеристика располагается в широком диапазоне частот, то ее график строят в логарифмическом масштабе по оси частот. Сначала проводят расчет точек на частотах f→0, f→∞, а далее, на частотах в логарифмическом масштабе `f =lg(f/f<sub>0</sub>), где`f=1,2, 3 и т.д. – нормированная частота в логарифмическом масштабе; f₀ – частота излома (частота среза) характеристики, выбранная за единицу; f/f₀=f_н - нормированная частота в абсолютном масштабе. Величина f₀ может быть принята любой.  В простейшем случае за f₀ можно принять 1Гц, или 1кГц. Однако если анализируется цепь первого порядка, то за f₀ принимают f₀=(2pt)^-1 (w₀=1/t), где t - постоянная времени цепи.

Если цепь имеет несколько постоянных времени, то ее ассимптотическая логарифмическая характеристика, состоит из нескольких прямых и имеет несколько точек излома, каждой из которых соответствует своя постоянная времени     t₁=1/w₁; t₂=1/w₂  и т. д. Выбрав одну из них за опорную, можно построить график в масштабе wt или lgwt.

При построении логарифмических частотных характеристик, более подробно, в каждой декаде следует брать по 3 –точки (0, 2, 5). Если необходимо, то проводят уточнение вблизи точек экстремумов - минимума или максимума, взяв по 10 точек вблизи них.

Особенности построения графиков ФЧХ.