Краткие теоретические сведения и методические советы по выполнению курсовой работы, страница 8

2.1.2 Путем последовательного исключения отдельных переменных, подстановок и повторного дифференцирования, систему уравнений состояния сводят к одному дифференциальному уравнению вида:

a_n,       (2.6)  где y- отклик, x- воздействие,  - постоянные коэффициенты, n - порядок дифференциального уравнения, зависит от числа реактивных элементов в схеме и способа их соединения.

2.2 Известно, что общее решение неоднородного линейного дифференциального уравнения (НЛДУ) состоит из двух частей:

y(t)= y_C(t) + y_B(t) ,                                                   (2.7)

где y_C(t) - общее решение линейного однородного дифференциального уравнения (ЛОДУ), полученное из ( 2.6 ) при x(t) = 0 ;   y _B(t)- частное решение НЛДУ.

Частное решение неоднородного уравнения y_B(t) зависит от внешнего воздействия x(t). Поэтому его называют вынужденным. За него часто принимают решение уравнения в установившемся режиме y_B(¥), то есть при t®¥. Если воздействие представляет собой скачок постоянного напряжения x(t)= E·1(t), то решение ищут путем анализа цепи по постоянному току, когда ω=0. Или, если известно выражение для комплексного коэффициента передачи цепи K(jw), то решение находят из выражения

y_{B(t ® ¥)} = K_{u(w ® 0)}E,                                                 ( 2.8 )

где K_u(0) - коэффициент передачи по напряжению на нулевой частоте (w = 0).

2.2.2. Общее решение линейного однородного дифференциального уравнения  (ЛОДУ) находится при x (t) = 0 . Оно характеризует собственные процессы в цепи, а поэтому называется собственным или свободным и ищется в виде:

,                            ( 2.9 )

где   A ₁, A ₂.....A_N  - постоянные коэффициенты, зависящие от начальных или граничных значений;  p ₁, p ₂ ...... p _N - корни характеристического уравнения. Его получают из однородного дифференциального уравнения заменой производных, как показано ниже:

        pⁿ + a_n-1 p^n-1+.....+ a₀ = 0                        ( 2.10 )

Характер решения (2.9) дифференциального уравнения зависит от характера корней уравнения (2.10). Рассмотрим возможные варианты решения для уравнения второго порядка (n=2), для более высоких порядков решение получается громоздким. Корнями уравнения (2.10), при n=2, являются:

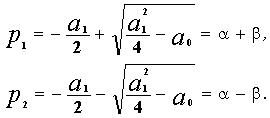                                    ( 2.11 )

Если:

a) Корни вещественны и равны:

,                                     (2.12)

б) Корни вещественны и неравны:

,                                      (2.13)

в) Корни мнимые:

     (2.14)

где                             ,                                                        

г) Корни комплексные:

      (2.15)

где  и  определяются согласно (2.14).

В пассивных цепях собственные колебания протекают под действием начальной энергии накопленной в виде зарядов емкостей или токов через индуктивность. С течением времени накопленная энергия переходит в тепловую. Поэтому собственные колебания затухают, а величина <0.

Существенным этапом решения ЛОДУ являются нахождение постоянных интегрирования А₁…А_n. Они определяются, исходя из начальных условий т.е. из состояния цепи при t=0, для искомой функции и ее производных. Определив при начальных условиях значения искомой функции y₍₀₎ и ее производных y¹₍₀₎, ..y^n-1₍₀₎ и подставив эти значения в формулу для общего решения (2.18) и ее производных, при t=0, получаем систему уравнений из решения которой и находятся значения А₁..А_n.

Для нахождения значений искомой функции и ее производных при t=0 следует учитывать следующие физические законы непрерывности (законы коммутации):

а) Закон непрерывности изменения магнитного потока. Из него следует, что ток через индуктивность, после изменения напряжения на ней, мгновенно изменяться не может т.е.

.                                        (2.16)

б) Закон непрерывности изменения заряда. Из него следует, что напряжение на емкости, при изменении тока протекающего через него, мгновенно измениться не может т.е.