Краткие теоретические сведения и методические советы по выполнению курсовой работы, страница 2

2. комплексная проводимость двухполюсника .(здесь - воздействием является напряжение - , а откликом- ток - =Y; параметр -  Y=1/Z=G+jB; где: G и B активная и реактивная составляющие проводимости двухполюсника).

1.2. Параметры четырехполюсника (Z_ВХ, Y_ВХ, K_U, K_i)

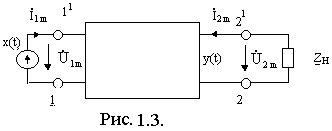
Для четырехполюсника (рис.1.3) все параметры могут быть разбиты на четыре группы :

1. входные параметры. По отношению к источнику сигнала четырехполюсник является двухполюсником, а потому имеет аналогичные ему параметры:

1) комплексное входное сопротивление  ;

2) комплексная входная проводимость .

2.  передаточные параметры. Они характеризуют передачу сигналов через четырехполюсник со входа на выход т. е. в прямом направлении:

1) комплексный коэффициент передачи напряжения  (=,=);

2) комплексный коэффициент передачи тока  , (,);

3) комплексное сопротивление прямой передачи  Z_n = U_2m/I_1m , (, ), или K_UI-коэффициент преобразования U в I ;

4) комплексная проводимость прямой передачи Y_m = I_2m/U_1m , (,). или K_IU-коэффициент преобразования I в U.

3.  Выходные параметры:

1)  комплексное выходное сопротивление ;

2)  комплексная выходная проводимость , где  - комплексная амплитуда выходного напряжения при холостом ходе на выходе (),  - комплексная амплитуда выходного тока при коротком замыкании () на выходе.

4.  Параметры обратной передачи. Они характеризуют передачу сигналов через четырехполюсник, с выхода на вход, т.е. в обратном направлении. Их названия аналогичны названиям передаточных параметров.

1.3. Частотные характеристики электрических цепей

Если в состав цепи входят реактивные элементы( L, C ), то из-за зависимости их сопротивлений от частоты гармонического сигнала параметры цепи становятся частотно-зависимыми. Зависимости параметров цепи от частоты гармонического воздействия называют частотными характеристиками, т.е. для каждого параметра цепи есть своя комплексная частотная характеристика (КЧХ). Названия частотным характеристикам дают в соответствии с названием параметра. Частотная характеристика цепи или комплексная функции цепи есть зависимость от частоты отношения комплексных амплитуд отклика и воздействия. Она может быть записана в показательной и алгебраической форме:

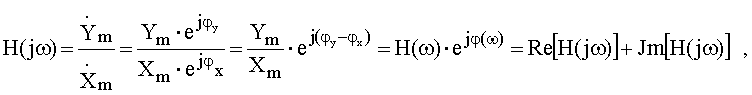           где  - амплитудно-частотная характеристика (АЧХ) (или модуль комплексной функции - |H(jw)|) - есть зависимость от частоты отношения амплитуд выходного и входного гармонических колебаний ;

j(w)=arctg[Jm[H(jw)] - фазо-частотная характеристика (ФЧХ) (или аргумент комплексной функции – arg(H(jw)) - есть зависимость от частоты разности фаз выходного и входного сигналов т.е. j(w)=j₂-j_1.

Re[ H(jw)]. Im[H(jw)] – реальная и мнимая части комплексной функции.

1.4. Расчет частотных характеристик

В основу расчета частотных характеристик положен метод комплексных амплитуд (МКА). Для простых цепей частотную характеристику находят, используя законы Ома и Кирхгофа. Для сложных функций при расчете частотных характеристик используют методы: эквивалентных преобразований, контурных токов, узловых потенциалов и др. Порядок применения метода МКА следующий:

1.  Гармонические токи и напряжения (x(t)=X_mcos(ωt-φ_x)) всех ветвей схемы заменить их комплексными амплитудами (X_m=X_me^-jφx), а от исходной схемы цепи составленной из элементов (R, L, C), перейти к комплексной схеме замещения с комплексными сопротивлениями (Z_R=R, Z_C=1/(jωC), Z_L= jωL).

2.  Составить уравнения электрического равновесия цепи для комплексных изображений токов и напряжений с использованием законов Ома и Кирхгофа или используя другие методы.

3.  Решить систему составленных уравнений относительно комплексных амплитуд интересующих токов или напряжений (Ý_m=Y_me^-jφx).

4.  Для нахождения комплексной частотной характеристики (КЧХ) записать отношение комплексной амплитуды отклика к комплексной амплитуде воздействия.